Hi guys
I'm working on an active speaker project and have hi and low pass filters on the input of each amp. It was easy to find online calculators for 1st order design but I'm having trouble with finding anything to design 2nd order filters. Can someone please point me in the direction of something to help design these second order filters.
I need 2nd order with a corner freq of 500hz.
Thanks

Sent from my SM-T800 using Tapatalk
I'm working on an active speaker project and have hi and low pass filters on the input of each amp. It was easy to find online calculators for 1st order design but I'm having trouble with finding anything to design 2nd order filters. Can someone please point me in the direction of something to help design these second order filters.
I need 2nd order with a corner freq of 500hz.
Thanks

Sent from my SM-T800 using Tapatalk
Look up Linkwitz-Reilly filters.
The phases are matched through these filters.
The levels between each speaker are matched too.
The phases are matched through these filters.
The levels between each speaker are matched too.
Last edited:
Hi,
If your working on an active (or any) speaker project
you need a lot more knowledge than online calculators.
Zaphaudio.com is a good place to start to understand.
If you can't do passive, you can't do active.
rgds, sreten.
If your working on an active (or any) speaker project
you need a lot more knowledge than online calculators.
Zaphaudio.com is a good place to start to understand.
If you can't do passive, you can't do active.
rgds, sreten.
Last edited:
Thanks guys,
Looks like the first resistor value is multiplied by 10 to give the second resistor value and the first cap value is divided by 10 to get the second cap value.
That's what I was looking for.
Cheers
Sent from my D5833 using Tapatalk
Looks like the first resistor value is multiplied by 10 to give the second resistor value and the first cap value is divided by 10 to get the second cap value.
That's what I was looking for.
Cheers
Sent from my D5833 using Tapatalk
For a second order passive RCR'C' filter one can get a Q = just under 0.5,
if R' >> R and C'R' = CR
Is it possible to create a Q value that is higher than 0.5?
How does one do that?
if R' >> R and C'R' = CR
Is it possible to create a Q value that is higher than 0.5?
How does one do that?
Crossover frequency quality
Without doing any formal analysis of your question, it would seem to me every time your up the order of the filter, the steepness of the cutoff frequency would increase. So wouldn't going from and R1C1R2C2 to an R1C1R2C2R3C3 help?
Without doing any formal analysis of your question, it would seem to me every time your up the order of the filter, the steepness of the cutoff frequency would increase. So wouldn't going from and R1C1R2C2 to an R1C1R2C2R3C3 help?
The Q gets lower as each CR stage is added.
The first order Butterworth has a Q of 0.7071 (although technically that is incorrect because those that know say the first order CR cannot have a Q value).
The second order RCRC drops the Q down to 0.5 ( it's two 0.7071 cascaded to give Q = 0.7071² = 0.5).
The third order RCRC would have a Q= 0.353
That equates to a very slow initial roll off that would sound wrong.
If you make the impedance of the first stage very much less than the impedance of the next stage you can raise the Q a bit. the same applies to the impedance ratios of 2nd:3rd.
But that is almost unusable: first RC could be 100r+1uF, then 1000r+100nF, then 10k+10nF
If your source cannot drive that 100r+1uF and you need to increase your first stage impedance, that cascades through all the following stages.
The first order Butterworth has a Q of 0.7071 (although technically that is incorrect because those that know say the first order CR cannot have a Q value).
The second order RCRC drops the Q down to 0.5 ( it's two 0.7071 cascaded to give Q = 0.7071² = 0.5).
The third order RCRC would have a Q= 0.353
That equates to a very slow initial roll off that would sound wrong.
If you make the impedance of the first stage very much less than the impedance of the next stage you can raise the Q a bit. the same applies to the impedance ratios of 2nd:3rd.
But that is almost unusable: first RC could be 100r+1uF, then 1000r+100nF, then 10k+10nF
If your source cannot drive that 100r+1uF and you need to increase your first stage impedance, that cascades through all the following stages.
Last edited:
Thanks Andrew
Any chance you could draw a 2nd order hi and low pass for me at 600hz?
Would really appreciate it if you could.
Cheers
Any chance you could draw a 2nd order hi and low pass for me at 600hz?
Would really appreciate it if you could.
Cheers
It is a while since I studied filters, but I believe only a second order filter has a Q. A first order filter has simply a corner frequency. A third order filter has two extra parameters, neither of which is Q. I hope I remembered that right!AndrewT said:The Q gets lower as each CR stage is added.
The first order Butterworth has a Q of 0.7071 (although technically that is incorrect because those that know say the first order CR cannot have a Q value).
The second order RCRC drops the Q down to 0.5 ( it's two 0.7071 cascaded to give Q = 0.7071² = 0.5).
The third order RCRC would have a Q= 0.353
Hence you can't combine Q's by multiplying, as Q is only defined for n=2.
Yes, it was you that had to correct me a long while back and I have not forgotten.It is a while since I studied filters, but I believe only a second order filter has a Q.
But when you combine two equal value RC into a cascaded pair to give an RCRC, you find that the Q has come out at 0.5A first order filter has simply a corner frequency. A third order filter has two extra parameters, neither of which is Q. I hope I remembered that right!
Hence you can't combine Q's by multiplying, as Q is only defined for n=2.
It appears that the resulting Q for the cascade appears to be 0.7071²
Which to me implies that one can assign a notional Q=0.07071 to the single pole version, even though all those that know say that an n=1 filter, can't have a Q value.
Assigning a notional value to a circuit parameter which does not exist (Q, when n=1) is not likely to be helpful, especially if this 'value' has been derived by considering a fictitious way of combining this non-existent parameter (multiply the Q's) when circuits are cascaded.
I studied physics over 20 years ago, I really have little practical experience with these things. What I had been taught about Q was that it was the center frequency divided by the bandwidth (-3db points in a notch or band pass). This is irregardless of the shape of the curve. If its asymmetric, I think most people use a geometric means f0 = sqrt(f1*f2). I am not familiar really with the concept of Q in low and high pass filters. What I was taught was the following:
Band pass or Band Reject has:
1) notch depth
2) center frequency
3) high and low cutoff frequencies.
of course the curves can look different, but again the most basic descriptors.
Notches might look different, but their all going to have a center and cutoff frequencies (so long as they notch below 3db)
2) low or high pass filters have a
a) cutoff frequency (-3db point or breakpoint)
b) slope or db per octave or decade
of course there are nonlinear type curves and everything else you can make especially digitally, but these are the most basic descriptors used to describe run of the mill filters.
From Wikipedia talks about initial Q, but then more rolloff:
A second-order filter attenuates high frequencies more steeply. The Bode plot for this type of filter resembles that of a first-order filter, except that it falls off more quickly. For example, a second-order Butterworth filter reduces the signal amplitude to one fourth its original level every time the frequency doubles (so power decreases by 12 dB per octave, or 40 dB per decade). Other all-pole second-order filters may roll off at different rates initially depending on their Q factor, but approach the same final rate of 12 dB per octave; as with the first-order filters, zeroes in the transfer function can change the high-frequency asymptote. See RLC circuit.
I don't have any experience with this initial Q in low and high pass filters, are they talking about how sharp the knee is near the cutoff frequency? Is there a simple definition for Q for low and high pass filters like there are for notches?
Band pass or Band Reject has:
1) notch depth
2) center frequency
3) high and low cutoff frequencies.
of course the curves can look different, but again the most basic descriptors.
Notches might look different, but their all going to have a center and cutoff frequencies (so long as they notch below 3db)
2) low or high pass filters have a
a) cutoff frequency (-3db point or breakpoint)
b) slope or db per octave or decade
of course there are nonlinear type curves and everything else you can make especially digitally, but these are the most basic descriptors used to describe run of the mill filters.
From Wikipedia talks about initial Q, but then more rolloff:
A second-order filter attenuates high frequencies more steeply. The Bode plot for this type of filter resembles that of a first-order filter, except that it falls off more quickly. For example, a second-order Butterworth filter reduces the signal amplitude to one fourth its original level every time the frequency doubles (so power decreases by 12 dB per octave, or 40 dB per decade). Other all-pole second-order filters may roll off at different rates initially depending on their Q factor, but approach the same final rate of 12 dB per octave; as with the first-order filters, zeroes in the transfer function can change the high-frequency asymptote. See RLC circuit.
I don't have any experience with this initial Q in low and high pass filters, are they talking about how sharp the knee is near the cutoff frequency? Is there a simple definition for Q for low and high pass filters like there are for notches?
The Linkwitz-Reilly active filter uses different RC's in series to get a better Q factor.
If f is the breakpoint wanted then the first stage is 75% of f and the second stage is 150% of f.
Simply using same RC's sequentially gives a poor Q.
If f is the breakpoint wanted then the first stage is 75% of f and the second stage is 150% of f.
Simply using same RC's sequentially gives a poor Q.
I don't understand what Q really is for a low pass filter.
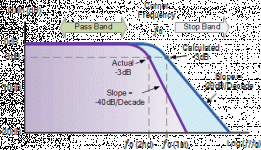
My question is really, what is the definition of Q for a low pass filter for example? I'm just asking because I don't know. Is it a measure of the slope of the curve at the -3db breakpoint? I see people talking about this a lot, but I haven't really found a definition that is intuitive.
For example here is a good basic article Low Pass Filter - Passive RC Filter Tutorial and I don't believe there is a mention of Q. Anyhow I have attached a figure from it, and as you said, you can see how the -3db point changes with the order of the filter, but this is nothing that you couldn't adjust in your design. But you wont get a flat response like the Linkwitz-Reilly in the crossover. When summed the butterworths have the center hump. But if its for a speaker system, you're probably not getting a flat response for most consumer type systems anyhow, a lot happens between the crossover and the ear.
The reason I'm chiming in is because I'm hoping someone will want to explain the concept of Q in low and high pass filters, it just seems a little nebulous to me at this point. I have seen damping and Q factors in equations, but I just don't understand what they're talking about.
Thank you Nigel for you're comments I have been learning a lot from your posts.
My question is really, what is the definition of Q for a low pass filter for example? I'm just asking because I don't know. Is it a measure of the slope of the curve at the -3db breakpoint? I see people talking about this a lot, but I haven't really found a definition that is intuitive.
For example here is a good basic article Low Pass Filter - Passive RC Filter Tutorial and I don't believe there is a mention of Q. Anyhow I have attached a figure from it, and as you said, you can see how the -3db point changes with the order of the filter, but this is nothing that you couldn't adjust in your design. But you wont get a flat response like the Linkwitz-Reilly in the crossover. When summed the butterworths have the center hump. But if its for a speaker system, you're probably not getting a flat response for most consumer type systems anyhow, a lot happens between the crossover and the ear.
The reason I'm chiming in is because I'm hoping someone will want to explain the concept of Q in low and high pass filters, it just seems a little nebulous to me at this point. I have seen damping and Q factors in equations, but I just don't understand what they're talking about.
Thank you Nigel for you're comments I have been learning a lot from your posts.
Attachments
I think that q is the gain at the breakpoint.
i.e. when RC's are the same you get 0.707 times 0.707 which is about 1/2
If you use different RC's as I mentioned earlier the gain is much better.
LR is good as you get 360 degrees phase shift through high and low pass filters.
Also as you got through the breakpoint the upper and lower signals sum to the same value in amplitude.
i.e. when RC's are the same you get 0.707 times 0.707 which is about 1/2
If you use different RC's as I mentioned earlier the gain is much better.
LR is good as you get 360 degrees phase shift through high and low pass filters.
Also as you got through the breakpoint the upper and lower signals sum to the same value in amplitude.
Last edited:
Here is one of my LR designs.
An externally hosted image should be here but it was not working when we last tested it.
- Status
- Not open for further replies.
- Home
- Source & Line
- Analog Line Level
- Filter design