Joe,
We simply have no time here for meta conversation.
You are not required to post here.
If you make a topical reply I will find it and respond.
😀
We simply have no time here for meta conversation.
You are not required to post here.
If you make a topical reply I will find it and respond.
😀
Hey, some people get all charged up when they get a chance to use their mental capacity to do work! 😉
Joe that wasn't aimed at you in particular. It was more of a joke about another person, another thread, another forum.
poobah said:
Joe that wasn't aimed at you in particular. It was more of a joke about another person, another thread, another forum.
Hey I just remebered something...
"The voltage in a cap cannot change instantaneously"
Implies mandatory resistance... SOMEWHERE.
"The voltage in a cap cannot change instantaneously"
Implies mandatory resistance... SOMEWHERE.
Tis true: i = C (dV/dt) because if voltage could change instantaneously then current would be infinite.
Yep!
And all this leads NO zero R AND L... which is the premise of the paradox. And also where the equations freak-out.
I remember now calculating the energy dissipated by a resistor charging a cap... equal to the final energy in the cap, and 1/2 of that applied to entire circuit.
So... no circuit without some R or L.
And all this leads NO zero R AND L... which is the premise of the paradox. And also where the equations freak-out.
I remember now calculating the energy dissipated by a resistor charging a cap... equal to the final energy in the cap, and 1/2 of that applied to entire circuit.
So... no circuit without some R or L.
I've been calculating charge and energy in caps for 25 years. It is a convenient way of solving steady state equations for switchers.
You guys suppose Choco is just hosing us???
😡
I was about to employ the "chewbacca defense".
Giaime,
Next time... punch your professor in the nose.
You guys suppose Choco is just hosing us???
😡
I was about to employ the "chewbacca defense".
Giaime,
Next time... punch your professor in the nose.
I'm with you on post 30. Which alludes to the "no R or L" fallacy.
You lost me on post 35 though.
I'm not really interested in calculating anything, been doing that forever, correctly it would seem... just explaining the paradox. As far as the missing energy is concerned... you gotta burn it (R and other things) or store it (L with some E & H into the ether). When you have neither, the paradox, which is BS, arises.
parlor tricks...
now
here's a parlor trick!
You lost me on post 35 though.
I'm not really interested in calculating anything, been doing that forever, correctly it would seem... just explaining the paradox. As far as the missing energy is concerned... you gotta burn it (R and other things) or store it (L with some E & H into the ether). When you have neither, the paradox, which is BS, arises.
parlor tricks...
now
here's a parlor trick!
One person has gotten this right- the Shark. The R and L stuff is a total red herring.
I'll push you a little further- charge is conserved. Energy isn't because it's not a closed system. In order to move charge around in the presence of fields, work has to be done. The sum of the cap energy and the work is equal to the original energy, so there's no 1st Law violation. All this (to me) is much clearer in my equivalent problems, but either way, work done in moving charges in a field MUST be accounted for.
poobah- I'm perfectly sober at the moment. I cannot say the same about last night. 😉
I'll push you a little further- charge is conserved. Energy isn't because it's not a closed system. In order to move charge around in the presence of fields, work has to be done. The sum of the cap energy and the work is equal to the original energy, so there's no 1st Law violation. All this (to me) is much clearer in my equivalent problems, but either way, work done in moving charges in a field MUST be accounted for.
poobah- I'm perfectly sober at the moment. I cannot say the same about last night. 😉
Hi Poobah !
No I am not tricking you. I am serious in this discussion.
But I do disagree a lot with the doug-smith paper.
His postualte that moving charge needs energy is correct, but this energy is then available in the charge and not lost.
We can move charge without losses. Just imagine a simple ideal resonant circuit. BTW, using a choke and two switches would allow us two transfer the energy lossless from C1 to C2... may be I will prepare a simulation.
Also the doug smith paper tells that the unit of capacitances would be a length. ...just hoping that this guy does not really believe all the stuff, which he is saying..... His formula is slightly strange from geometrics anyway and especially it is missing the natural electric field constant which is 8.859 E-12 F/m .
I do also not fully agree to post 30, because in theory we can have zero resistance. And in theory we can have indefinite high currents for indefinite short times. Normally we solve such division by zero or multiplication by indefinite terms by several math tools (i.e. de l'hopital). But in our case it is much easier, because the R is droping from the equation. For me this means the losses do happen, no matter which resistance we are putting there.
Let's make it simpler. Just one cap which is charged in the beginning and then short circuited by zero Ohms. We will again get the same phenomenon of lost energy.
Also forget about thinking if we loose the energy in some inductance, which we might suspect instead of a resistance.
If we would apply an ideal inductance instead of our zero Ohms, then we will have an ideal resonant circuit, which is ringing at its resonant frequency and is loosing no energy at all and does never stop to ring.
Burnedfingers:
Trying to understand theory is sometimes helpful to avoid burning fingers. 😀 So we are not wasting our time.
No I am not tricking you. I am serious in this discussion.
But I do disagree a lot with the doug-smith paper.
His postualte that moving charge needs energy is correct, but this energy is then available in the charge and not lost.
We can move charge without losses. Just imagine a simple ideal resonant circuit. BTW, using a choke and two switches would allow us two transfer the energy lossless from C1 to C2... may be I will prepare a simulation.
Also the doug smith paper tells that the unit of capacitances would be a length. ...just hoping that this guy does not really believe all the stuff, which he is saying..... His formula is slightly strange from geometrics anyway and especially it is missing the natural electric field constant which is 8.859 E-12 F/m .
I do also not fully agree to post 30, because in theory we can have zero resistance. And in theory we can have indefinite high currents for indefinite short times. Normally we solve such division by zero or multiplication by indefinite terms by several math tools (i.e. de l'hopital). But in our case it is much easier, because the R is droping from the equation. For me this means the losses do happen, no matter which resistance we are putting there.
Let's make it simpler. Just one cap which is charged in the beginning and then short circuited by zero Ohms. We will again get the same phenomenon of lost energy.
Also forget about thinking if we loose the energy in some inductance, which we might suspect instead of a resistance.
If we would apply an ideal inductance instead of our zero Ohms, then we will have an ideal resonant circuit, which is ringing at its resonant frequency and is loosing no energy at all and does never stop to ring.
Burnedfingers:
Trying to understand theory is sometimes helpful to avoid burning fingers. 😀 So we are not wasting our time.
SY, no.
Without field we can easily move charge without changing the potential energy of the charge.
If there is a field, then the might be a change of potential energy depending on the direction in which we move the charge. Furtheron not only the potential energy may change but also the mechanical energy (i.e. brown tube... speed of electrons).
Look at an simple resonant circuit, there we can move the charge without any losses. Theoretically an ideal resonant circuit will never stop to ring. Sometimes you will have all the energy in the cap (high voltage), sometimes you will have all the energy in the choke (high current). But we don't loose it.
Even an lossy resonant circuit allows to transfer much more charge than the Doug Smith paper would allow.
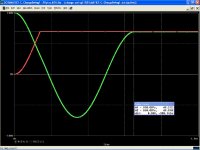
Look to the attached simulation. It is lossy due to switches, which have Ron= 1 Ohm, Roff = 1meg Ohm and further switching losses, because this primitive circuit does not work all with soft switching.
Even in this lossy arangement we are able to transfer the energy from one C1 to C2 in a way that is ending up in almost perfect match to the ideal result of law of preserving energy.
Without field we can easily move charge without changing the potential energy of the charge.
If there is a field, then the might be a change of potential energy depending on the direction in which we move the charge. Furtheron not only the potential energy may change but also the mechanical energy (i.e. brown tube... speed of electrons).
Look at an simple resonant circuit, there we can move the charge without any losses. Theoretically an ideal resonant circuit will never stop to ring. Sometimes you will have all the energy in the cap (high voltage), sometimes you will have all the energy in the choke (high current). But we don't loose it.
Even an lossy resonant circuit allows to transfer much more charge than the Doug Smith paper would allow.
Look to the attached simulation. It is lossy due to switches, which have Ron= 1 Ohm, Roff = 1meg Ohm and further switching losses, because this primitive circuit does not work all with soft switching.
Even in this lossy arangement we are able to transfer the energy from one C1 to C2 in a way that is ending up in almost perfect match to the ideal result of law of preserving energy.
Attachments
Simulation results:
(If you do not believe the results, pick the old school books, invest some hours and calculate by hand)
(If you do not believe the results, pick the old school books, invest some hours and calculate by hand)
A resonant circuit is not an apt analogy because you're exchanging energy back and forth in a closed system. This is purely a matter of doing work, and the 1st Law demands that the final energy equal the original energy minus work.
Interestingly, you can also consider this problem from an entropy standpoint; think of an isothermal expansion...
Interestingly, you can also consider this problem from an entropy standpoint; think of an isothermal expansion...
Resonant Circuit:
Do we move charge within a field? Yes.
Do we have losses? In an ideal resonant circuit, No.
So we can move charge in a field without losses.
Do we move charge within a field? Yes.
Do we have losses? In an ideal resonant circuit, No.
So we can move charge in a field without losses.
- Status
- Not open for further replies.