I agree, except I think that topology, as expressed by the toroid, is more about boundaries, i.e., whether or not the Universe has an edge.
It is often said that the terms elliptical, hyperbolic and flat refer to the 'shape' of the Universe, when in fact they refer to its 'local geometry'.
We are used to the concept of a 'flat local geometry'. The surface of the Earth looks flat to we who live on its surface, but this local view does not tell us the global geometry of the Earth, i.e., is it an infinite plane, a sphere or a torus?
To picture the actual 'shape' of the Universe we must refer to both its local geometry and its 'global geometry' - its 'topology'.
https://physics.aps.org/articles/v17/74
Apollo 8 astronaut Bill Anders, who took the iconic 'Earthrise' photograph, has died in a plane crash at the age of 90.
The photo was taken on Christmas Eve 1968 when the Apollo 8 crew went "Round the Moon and back..."
Speaking of the moment, Anders said: "We came all this way to explore the Moon, and the most important thing that we discovered was the Earth."
https://www.bbc.co.uk/news/articles/cw99wj5e5q8
The photo was taken on Christmas Eve 1968 when the Apollo 8 crew went "Round the Moon and back..."
Speaking of the moment, Anders said: "We came all this way to explore the Moon, and the most important thing that we discovered was the Earth."
https://www.bbc.co.uk/news/articles/cw99wj5e5q8
Fixed link for you: https://www.bbc.co.uk/news/articles/cw99wj5e5q8o
He was alone in the airplane when it crashed. Which shows some pluckiness to fly at age 90.
He once said that he estimated his chances of dying on Apollo 8 at 1 in 3, which shows the courage of those guys.
Usual shot tonight... no luck.
I am still thoroughly confused about the Flatness Problem:
The links in the quote should tell you more.
I am currently slowly working through Sean Carroll's book on Quanta and Fields and it is very interesting. Am getting a feel for how Quantum Fields are a collection of harmonic oscillators, and matter is merely an excitation of them.
But it is all about the ACTION S. And Hamiltonians H as the sum of energies. I am weak on this, so am thinking about pendulums of all things. Period T = 2 Pi x SQRT (L / g) for small angles if you recall.
It's about 2 seconds for a meter pendulum.
https://phys.libretexts.org/Bookshelves/Classical_Mechanics/Variational_Principles_in_Classical_Mechanics_(Cline)/15:_Advanced_Hamiltonian_Mechanics/15.05:_Action-angle_Variables
When you change the length of the pendulum slowly, say, halve it, everything changes as you'd expect. What you don't expect is that there is a conserved quantity called the Adiabatic Invariant.
Arnold Sommerfeld (with another cigar) knew all this stuff and his elliptical orbits worked like this too.
https://galileo-unbound.blog/2020/02/18/bohrs-orbits/
That is really a very interesting article. See his elliptical orbits were not the right interpretation, we now know what the wave functions do look like, but the maths was right!
Which kinda shows how much trouble we get into trying to visualise things like quantum mechanics. Or cosmology.
He was alone in the airplane when it crashed. Which shows some pluckiness to fly at age 90.
He once said that he estimated his chances of dying on Apollo 8 at 1 in 3, which shows the courage of those guys.
Usual shot tonight... no luck.
I am still thoroughly confused about the Flatness Problem:
A flat Universe is one in which the amount of matter present is just sufficient to halt its expansion, but insufficient to re-collapse it. This would represent a very fine balancing act indeed! Imagine the surprise of astronomers to find that, as near as we can tell, the Universe has exactly the required density of matter to be flat. This seems like a truly remarkable coincidence and has become known as the ‘flatness problem’.
To phrase it more scientifically, the flatness problem arises because we appear to live in a Universe that has an observed a density parameter (Ω0) very close to 1. In other words, the Universe is very close to the critical density. The ‘problem’ is that for the Universe to be so close to critical density after ~ 14 billion years of expansion and evolution, it must have been even closer at earlier times. For instance, it requires the density at the Planck time (within 10-43 seconds of the Big Bang) to be within 1 part in 1057 of the critical density. i.e. Ω0 initially must have been almost exactly:
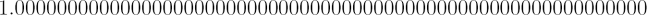
There is no known reason for the density of the Universe to be so close to the critical density, and this appears to be an unacceptably strange coincidence in the view of most astronomers. Hence the flatness ‘problem’.
Many attempts have been made to explain the flatness problem, and modern theories now include the idea of inflation which predicts the observed flatness of the Universe. However, not all scientists have accepted inflation, and the matter remains a subject of much debate and research.
The links in the quote should tell you more.
I am currently slowly working through Sean Carroll's book on Quanta and Fields and it is very interesting. Am getting a feel for how Quantum Fields are a collection of harmonic oscillators, and matter is merely an excitation of them.
But it is all about the ACTION S. And Hamiltonians H as the sum of energies. I am weak on this, so am thinking about pendulums of all things. Period T = 2 Pi x SQRT (L / g) for small angles if you recall.
It's about 2 seconds for a meter pendulum.
https://phys.libretexts.org/Bookshelves/Classical_Mechanics/Variational_Principles_in_Classical_Mechanics_(Cline)/15:_Advanced_Hamiltonian_Mechanics/15.05:_Action-angle_Variables
When you change the length of the pendulum slowly, say, halve it, everything changes as you'd expect. What you don't expect is that there is a conserved quantity called the Adiabatic Invariant.
Arnold Sommerfeld (with another cigar) knew all this stuff and his elliptical orbits worked like this too.
https://galileo-unbound.blog/2020/02/18/bohrs-orbits/
That is really a very interesting article. See his elliptical orbits were not the right interpretation, we now know what the wave functions do look like, but the maths was right!
Which kinda shows how much trouble we get into trying to visualise things like quantum mechanics. Or cosmology.
In a classical oscillator like a pendulum, the lowest potential energy level is zero as illustrated by the black line in the diagram below which is in the form of a potential well.
However the lowest energy state of a quantum oscillator, due to uncertainty, is not zero as shown by the red line.
Note the discrete, or quantised, set of energy levels which are in contrast to the continually changing levels of the classical oscillator.
I submitted this earlier in the thread, to a resounding silence of indifference!
Like Hamiltonian mechanics, Lagrangian mechanics looks at motion in terms of energy.
Where Hamiltonian mechanics considers the sum of the kinetic energy and potential energy of a system, Lagrangian mechanics considers the difference.
Lagrangian Mechanics says objects move between two points in a gravitational field in such a way as to minimise a quantity called the action.
It turns out that the action describes a path or trajectory through space and time.
For the (very) eager scholar, it's all explained here: https://profoundphysics.com/lagrangian-mechanics-for-beginners/
Quote:
As seen in this plot for a pendulum:
Last edited:
I think of a harmonic oscillator as one in which energy is stored in two different ways, and then exchanged between the two stores. For example, in a pendulum, it has potential energy at the extremes when the pendulum is furthest away from the earth's surface while at the bottom of its swing, it has kinetic energy. The two forms of energy are exchanged during the process of oscillation. Similarly, in a tank circuit, energy is stored either capacitively, or inductively and exchanged between the two. You can use this to understand how a spring works as well.
You mention a harmonic oscillator, but go on to describe a pendulum which is a classical oscillator.
In a harmonic oscillator the energy levels are quantised, unlike the potential energy levels of a pendulum which are continually changing.
EDIT: What you were describing is called a 'Simple Harmonic Oscillator' while Steve was looking at the 'Quantum Harmonic Oscillator'.
https://en.wikipedia.org/wiki/Quant... important model systems in quantum mechanics.
Last edited:
Talking about energy conservation, I read that energy is not conserved in an expanding Universe.
https://bigthink.com/starts-with-a-bang/expanding-universe-conserve-energy/
Underlying energy conservation is the requirement that physical properties and laws don’t evolve with time. However the distance between any two cosmic objects that aren’t gravitationally bound together does evolve with time.
That implies that energy is no longer conserved in an expanding Universe! Only if the Universe were static, i.e. looked the same backwards and forwards in time, would energy be conserved. However, since the Universe is expanding and changing in time it does not meet this criterion for energy conservation.
Apparently, all this is courtesy of Noether's (first) theorem which relates Conservation Laws to Lagrangian Mechanics and the Action of a physical system.
To complete the above sentence, "if a system has a continuous symmetry property, then there are corresponding quantities whose values are conserved in time".
https://bigthink.com/starts-with-a-bang/expanding-universe-conserve-energy/
Underlying energy conservation is the requirement that physical properties and laws don’t evolve with time. However the distance between any two cosmic objects that aren’t gravitationally bound together does evolve with time.
That implies that energy is no longer conserved in an expanding Universe! Only if the Universe were static, i.e. looked the same backwards and forwards in time, would energy be conserved. However, since the Universe is expanding and changing in time it does not meet this criterion for energy conservation.
Apparently, all this is courtesy of Noether's (first) theorem which relates Conservation Laws to Lagrangian Mechanics and the Action of a physical system.
To complete the above sentence, "if a system has a continuous symmetry property, then there are corresponding quantities whose values are conserved in time".
Last edited:
That's understandable since Steve moved quickly from mentioning quantum fields and harmonic oscillators to thinking about pendulums.
This would imply that the total energy of the cosmos is changing - a fundamental break with the laws of physics as we know them surely.
Or, could it be that, from E=mc^2, we can say the total energy in the cosmos is constant, but, through all energy transformations taking place in the cosmos, it gives rise to time, which as I have said before on these pages, we see as distance (cf space-time). Lee Smolin's 'Time Reborn' btw is a fascinating journey into one of the biggest reasons modern physics is in turmoil: we've removed time as a 'thing' and made it something that is independent and divorced from all other physical phenomena. But, you cannot think about energy being transformed without it involving time - the two are as linked as space-time is.
Thankfully, there is a 'get-out clause' at the end of my earlier link.
Only if physical properties and laws don’t evolve with time can energy be defined.
It therefore follows that energy has no unique definition in an expanding spacetime!
As I grapple with Lagrangian Mechanics, thoughts of an expanding Spacetime (that's the Notorious Ethan Siegel again isn't it?) to also incorporate are hardly helpful!
Maybe how my hypothetical shortening pendulum behaves in such a scenario can be done, but I'd rather keep it simple at this very undergraduate stage.
Joseph-Louis Lagrange was a very bright man. He was recommended by the incomparable Euler to succeed him at Berlin University.
Euler found 3 of what are now called Lagrange points, Lagrange added L4 and L5. IIRC, he also analysed the extraordinary 1:2:4 resonance of the moons Io, Europa and Ganymede around Jupiter.
Interestingly, the latest simulations say that Callisto will join the club soon to make it 1:2:4:8, and then it will all be stable for the next 1.5 Bn years.
I also like his discovery that any integer can be expressed as the sum of 4 squares. This may help in 4D Special Relativity.
TBH, I thought it was Hamiltonian Mechanics, T+V, used in Quantum Field Theory, but must now re-evaluate as T-V, and Sean Carroll is definitely using Lagrangians.
Just for the record, I checked what the Ground State Energy of a Quantum Harmonic Oscillator is:
I like to assemble all the relevant pieces, then try to fit it all together. Don't you?
Best, Steve.
Maybe how my hypothetical shortening pendulum behaves in such a scenario can be done, but I'd rather keep it simple at this very undergraduate stage.
Joseph-Louis Lagrange was a very bright man. He was recommended by the incomparable Euler to succeed him at Berlin University.
Euler found 3 of what are now called Lagrange points, Lagrange added L4 and L5. IIRC, he also analysed the extraordinary 1:2:4 resonance of the moons Io, Europa and Ganymede around Jupiter.
Interestingly, the latest simulations say that Callisto will join the club soon to make it 1:2:4:8, and then it will all be stable for the next 1.5 Bn years.
I also like his discovery that any integer can be expressed as the sum of 4 squares. This may help in 4D Special Relativity.
TBH, I thought it was Hamiltonian Mechanics, T+V, used in Quantum Field Theory, but must now re-evaluate as T-V, and Sean Carroll is definitely using Lagrangians.
Just for the record, I checked what the Ground State Energy of a Quantum Harmonic Oscillator is:
I like to assemble all the relevant pieces, then try to fit it all together. Don't you?
Best, Steve.
One of the fundamental tenets of physics is that the laws of nature are the same everywhere. After all, science has been able to fairly accurately deconstruct the events around the BB using the standard model and that occurred 13.8 billion yrs ago in a ‘far away place’. It will require a complete rewriting of physics to throw out the idea that energy has no unique definition or that the total energy in the cosmos is not constant. I imagine the energy density is changing, but not total energy.
That's pretty much how energy conservation would be taught in a high school physics course.
It's nice to receive a submission that is easy to understand for a change!