As matter falls into a black hole, it increases the black hole's spin, but there's a limit to how much angular momentum it can possess,
The spin speed of a black hole is assigned a value between 0 and 1, with 1 being a significant fraction of the speed of light.
Sgr A* has a spin value of between 0.84 and 0.96 - close to the maximum possible speed as defined by a black hole's width.
I read it here: https://www.space.com/milky-way-supermassive-black-hole-cosmic-speed-limit
I've unearthed more information about the orbit of star S2 around Sgr A*.
Observations show that it orbits exactly as predicted by Einstein's theory of general relativity.
S2's orbit is actually shaped like a rosette and not like a simple ellipse as predicted by Newton's theory of gravity.
The effect is known as Schwarzschild precession, shown exaggerated in the above artist's impression.
The location of S2's closest-approach point changes with each lap, so the overall orbit is shaped like a rosette rather than a simple, static ellipse.
https://www.space.com/milky-way-supermassive-black-hole-star-dance-einstein-test.html
Observations show that it orbits exactly as predicted by Einstein's theory of general relativity.
S2's orbit is actually shaped like a rosette and not like a simple ellipse as predicted by Newton's theory of gravity.
The effect is known as Schwarzschild precession, shown exaggerated in the above artist's impression.
The location of S2's closest-approach point changes with each lap, so the overall orbit is shaped like a rosette rather than a simple, static ellipse.
https://www.space.com/milky-way-supermassive-black-hole-star-dance-einstein-test.html
It's interesting that you liken the rotation of a galaxy to a spinning top.
As you will know, a spinning top can undergo precession - it can wobble about its spin axis.
The fact that the outer disc of the Milky Way galaxy is warped has been known for decades - see visualisation below.
According to the data, the warp would complete one rotation around the centre of the Milky Way in about 600 million years. (By comparison, the sun makes one orbit around the galactic centre in about 200 million years.)
However, there is evidence that the warp is not static, but precesses - meaning that just like a spinning top the orientation of its axis is wobbling.
https://www.sciencedaily.com/releases/2021/05/210525101722.htm
No need to go that far and need a BH.
An apsidal precession of the planet Mercury was noted by Urbain Le Verrier in the mid-19th century and accounted for by Einstein's general theory of relativity.
Einstein showed that for a planet, the major semi-axis of its orbit being a, the eccentricity of the orbit e and the period of revolution T, then the apsidal precession due to relativistic effects, during one period of revolution in radians.......
To get the formula, google for Wikipedia Mercury precession.
.........where c is the speed of light. In the case of Mercury, half of the greater axis is about 5.79×1010 m, the eccentricity of its orbit is 0.206 and the period of revolution 87.97 days or 7.6×106 s. From these and the speed of light (which is ~3×108 m/s), it can be calculated that the apsidal precession during one period of revolution is ε = 5.028×10−7 radians (2.88×10−5 degrees or 0.104″). In one hundred years, Mercury makes approximately 415 revolutions around the Sun, and thus in that time, the apsidal perihelion due to relativistic effects is approximately 43″, which corresponds almost exactly to the previously unexplained part of the measured value.
An apsidal precession of the planet Mercury was noted by Urbain Le Verrier in the mid-19th century and accounted for by Einstein's general theory of relativity.
Einstein showed that for a planet, the major semi-axis of its orbit being a, the eccentricity of the orbit e and the period of revolution T, then the apsidal precession due to relativistic effects, during one period of revolution in radians.......
To get the formula, google for Wikipedia Mercury precession.
.........where c is the speed of light. In the case of Mercury, half of the greater axis is about 5.79×1010 m, the eccentricity of its orbit is 0.206 and the period of revolution 87.97 days or 7.6×106 s. From these and the speed of light (which is ~3×108 m/s), it can be calculated that the apsidal precession during one period of revolution is ε = 5.028×10−7 radians (2.88×10−5 degrees or 0.104″). In one hundred years, Mercury makes approximately 415 revolutions around the Sun, and thus in that time, the apsidal perihelion due to relativistic effects is approximately 43″, which corresponds almost exactly to the previously unexplained part of the measured value.
No claim of originality for the verification of Einstein's general relativity (GR) was made in the case of star S2. 😉
In simple speak, GR was able to explain the difference between the expected precession of Mercury's apsides and the actual observations.
P.S. For those who don't know, the apsides refer to the farthest (A) and nearest (B) points reached by Mercury with respect to the Sun.
The apsides are called aphelion (farthest) and perihelion (nearest).
And I understand the Sun moves a bit too. Pesky stuff this gravity, Everything effects everything else.
Another interesting aspect
https://universe.nasa.gov/stars/multiple-star-systems/
That Hubble image I mentioned looked to show loads in some sort of orbital motion.
Another interesting aspect
https://universe.nasa.gov/stars/multiple-star-systems/
That Hubble image I mentioned looked to show loads in some sort of orbital motion.
That would imply there is an ergosphere in the volume between the outer and inner event horizons that Bonsai is so anxious to inhabit.
However I read that, as well as the outer ergosphere that lies outside the outer horizon, there is an inner ergosphere that lies inside the inner horizon.
The information is in the following link under the heading, 1. Ergospheres.
https://ysjournal.com/physics/kerr-...event horizon depending on the zenith angle.
Whatever, Kerr himself now appears to doubt the internal geometry of a Kerr black hole!
I remember discussing multiple star systems with Steve on the Artemis thread.
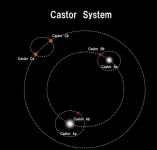
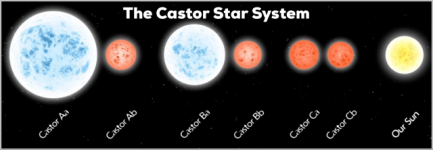
The six stars in the above system are organised in 3 close binaries which then orbit each other.
The Castor star system is another example of a sextuple system - images attached.
Attachments
In his recent paper, Kerr is actually referring to the singularity.
He says there is no proof that the metric is singular in any specified way, and that singularity believers need to provide such proof.
He offers the possibility that, instead of a singularity, a nonsingular Kerr metric exists within the inner event horizon, and suggests that nonsingular collapsed neutron stars can generate the Kerr metric.
https://www.researchgate.net/publication/375744216_Do_Black_Holes_have_Singularities
You won't be surprised to learn that practically all of Kerr's paper lies totally beyond my understanding!
Nice pictures in this thread recently. I like orbital mechanics. It can surprise you.
I found a short video of the Leona Betelgeuse occultation from Spain:
https://en.wikipedia.org/wiki/319_Leona
Quite hard to see, but it did go dimmer... 🙂
I found a short video of the Leona Betelgeuse occultation from Spain:
https://en.wikipedia.org/wiki/319_Leona
Quite hard to see, but it did go dimmer... 🙂
re Balck holes: One can’t help wondering what exactly the very center of a black hole comprises. I imagine the atoms are stripped of their electrons and the nuclei of atoms might survive in tact, but maybe the nucleus is broken down to component parts. Obvious matter inside the black hole is not destroyed or burned up, etc. It’s possible the atomic particles are subjected to tremendous squeezing forces so perhaps the particles are squished like pancakes or ribbons. But how big could an electron pancake be, worst case. Not too big. 🥞
The popular view is that matter is squashed out of existence at a point singularity, i.e., is removed from time and space as we conceive them to be.
A rotating (Kerr) black hole stretches the point singularity into a ring singularity through which matter (according to Einstein's GR) could rush out and emerge in an entirely new region of the Universe!
Truth is we don't (and may never) know what is going on inside a black hole.
Easier to understand is a neutron star which has no singularity, but where electrons and protons are squashed together by gravity to form neutrons.
In some ways, a neutron star can be likened to a giant nucleus, but one comprising mainly of neutrons.
However, it is not understood what is at the centre of a neutron star where the pressure is greatest. Some say that there we would find strange particles called hyperons: https://www.mdpi.com/2218-1997/7/11...features of the interaction between particles.
The same GR mathematics I referred to in my previous post allows a scenario where the interior of a rotating black hole is unstable.
In a Kerr black hole, the singularity is stretched into a ring which rotates at a rapid rate. This exerts such an incredibly large centrifugal force on matter approaching the ringularity that it acts like antigravity and oppose its fall into the black hole.
This is what forms the inner horizon, outside of which matter that was pulled by gravity toward the singularity will be pushed outward.
Therefore, in your scenario, you would indeed remain trapped between the inner and outer horizons.
But I presume squashed flat by centrifugal force unless you were in a really big BH like the one at the centre of M87?
I'm not sure if my ramblings interpret the rambling of others correctly! What is certain is that I am not fit to tie the shoelaces of Roy Kerr!
More googling indicates that it is light that I should be talking about in connection with the inner horizon:
The inner horizon forms a turning point at which the black hole's gravity is strong enough to keep light from leaving, but not strong enough to drag it all the way to the ringularity.
I can only presume this "turning point" ties in with my above description of an "antigravity" effect that weakens the gravitational pull of the ringularity.
So the light becomes trapped, and they say if you were to approach the inner horizon, a wall of intense radiation would blast you to smithereens!
https://astronomy.stackexchange.com...is-the-inner-horizon-of-a-rotating-black-hole
More googling indicates that it is light that I should be talking about in connection with the inner horizon:
The inner horizon forms a turning point at which the black hole's gravity is strong enough to keep light from leaving, but not strong enough to drag it all the way to the ringularity.
I can only presume this "turning point" ties in with my above description of an "antigravity" effect that weakens the gravitational pull of the ringularity.
So the light becomes trapped, and they say if you were to approach the inner horizon, a wall of intense radiation would blast you to smithereens!
https://astronomy.stackexchange.com...is-the-inner-horizon-of-a-rotating-black-hole
I guess this precession is taking place because of frame dragging, which is distorting spacetime in the region of the BH?
You see a similar thing with neutron stars where the equatorial angular velocity is at relativistic speeds.
Light cannot escape because spacetime is too warped and wrapped into itself like a huge vortex light has no pathway out. Besides photons have no mass. Light is not bent by gravity in the traditional sense.
If atomic particles were crunched out of existence in the singularity there could not be a super-massive singularity.
If atomic particles were crunched out of existence in the singularity there could not be a super-massive singularity.