Software Distortion Compensation for Measurement Setup
Hi,
I am thinking about options for some sort of digital compensation of harmonic distortion within the measurement loop (DAC -> ADC). E.g. ESS DAC chips offer second and third harmonic distortion compensation.
I have played with virtual balanced measurement setup Virtual balanced in/out from regular soundcard in linux - results which produces very good results, if properly calibrated. The principle is simple - each input channel has a precisely calibrated software gain element in the chain and difference of the left/right samples is provided to audio applications through a virtual sound capture device (very simple to achieve in linux).
I am thinking of the very same principle for some basic digital harmonic distortion compensation. Initial calibration of the measurement loop would measure the loop performance and generate configuration parameters. Parameters would be used in some non-linear gain component in the input chain (very likely a modified linux alsa route plugin reading multiple gain coefficients - I can handle that).
I understand a simple non-linear gain compensates only gain non-linearities of the loop but that would be a good start, IMO.
I found a relevant very interesting paper http://jrossmacdonald.com/jrm/wp-content/uploads/052DistortionReduction.pdf which deals with calculation of the non-linear compensation gain coefficients.
Please does anyone have any relevant experience/suggestion/theoretical background in this area? IMO this feature is possible to implement, leading to better-precision measurements with a regular prosumer-level equipment.
I very much appreciate any input.
Hi,
I am thinking about options for some sort of digital compensation of harmonic distortion within the measurement loop (DAC -> ADC). E.g. ESS DAC chips offer second and third harmonic distortion compensation.
I have played with virtual balanced measurement setup Virtual balanced in/out from regular soundcard in linux - results which produces very good results, if properly calibrated. The principle is simple - each input channel has a precisely calibrated software gain element in the chain and difference of the left/right samples is provided to audio applications through a virtual sound capture device (very simple to achieve in linux).
I am thinking of the very same principle for some basic digital harmonic distortion compensation. Initial calibration of the measurement loop would measure the loop performance and generate configuration parameters. Parameters would be used in some non-linear gain component in the input chain (very likely a modified linux alsa route plugin reading multiple gain coefficients - I can handle that).
I understand a simple non-linear gain compensates only gain non-linearities of the loop but that would be a good start, IMO.
I found a relevant very interesting paper http://jrossmacdonald.com/jrm/wp-content/uploads/052DistortionReduction.pdf which deals with calculation of the non-linear compensation gain coefficients.
Please does anyone have any relevant experience/suggestion/theoretical background in this area? IMO this feature is possible to implement, leading to better-precision measurements with a regular prosumer-level equipment.
I very much appreciate any input.
Last edited:
I am skeptical. If you read the McDonald paper, he admits that it is only useful in cases where negative feedback cannot be used or cannot be used easily.
Even then (the example of a speaker), distortion reduction is only limited effective, over a limited range of levels and frequencies.
For an ADC/DAC, distortion levels are often below -120dB and it is hard to imagine that a) it is possible to find an expression of the remaining non-linearity or b) precise modelling of that distortion, which would be required for pre- or post inverse distortion. Even when it is possible, you would need to apply the correction to an accuracy of at least better than -120dB.
I don't think this is physically possible with the current state of the art.
Jan
Even then (the example of a speaker), distortion reduction is only limited effective, over a limited range of levels and frequencies.
For an ADC/DAC, distortion levels are often below -120dB and it is hard to imagine that a) it is possible to find an expression of the remaining non-linearity or b) precise modelling of that distortion, which would be required for pre- or post inverse distortion. Even when it is possible, you would need to apply the correction to an accuracy of at least better than -120dB.
I don't think this is physically possible with the current state of the art.
Jan
Thanks a lot for your valuable opinion. Before replying I have to emphasize I do not know the algorithm for calculation of coefficients of the non-linear gain polynom, hopefully not yet 🙂
That is the case of reducing measurement loop distortion too, we cannot apply negative feedback here.
I can imagine the calibration would hold only for a specific frequency, used for the actual DUT measurement. After changing frequency the loop could be recalibrated. That would hold only for specific frequency measurements, no wideband/noise input signal of course. But a single or dual frequency are the most common measurement modes.
That is the question I am asking 🙂
For now I am aiming at compensating a non-linear gain on a specific frequency with a several orders-long polynom.
I do not think the actual accuracy of calculation would be an issue, calculating the polynomial expansion with float32 would easily provide precision > -120dB. Just the coefficients need to be determined with sufficient precision. But FFT can calculate the rms value of each harmonic component signal rather precisely plus we can average the values for several seconds of stream.
I am skeptical. If you read the McDonald paper, he admits that it is only useful in cases where negative feedback cannot be used or cannot be used easily.
That is the case of reducing measurement loop distortion too, we cannot apply negative feedback here.
Even then (the example of a speaker), distortion reduction is only limited effective, over a limited range of levels and frequencies.
I can imagine the calibration would hold only for a specific frequency, used for the actual DUT measurement. After changing frequency the loop could be recalibrated. That would hold only for specific frequency measurements, no wideband/noise input signal of course. But a single or dual frequency are the most common measurement modes.
For an ADC/DAC, distortion levels are often below -120dB and it is hard to imagine that a) it is possible to find an expression of the remaining non-linearity
That is the question I am asking 🙂
or b) precise modelling of that distortion, which would be required for pre- or post inverse distortion.
For now I am aiming at compensating a non-linear gain on a specific frequency with a several orders-long polynom.
Even when it is possible, you would need to apply the correction to an accuracy of at least better than -120dB.
I don't think this is physically possible with the current state of the art.
I do not think the actual accuracy of calculation would be an issue, calculating the polynomial expansion with float32 would easily provide precision > -120dB. Just the coefficients need to be determined with sufficient precision. But FFT can calculate the rms value of each harmonic component signal rather precisely plus we can average the values for several seconds of stream.
I do not think the actual accuracy of calculation would be an issue, calculating the polynomial expansion with float32 would easily provide precision > -120dB. Just the coefficients need to be determined with sufficient precision. But FFT can calculate the rms value of each harmonic component signal rather precisely plus we can average the values for several seconds of stream.
Good point. It's an interesting idea. I know that Klippel has done what your idea is, for speaker drivers.
I will follow your adventure!
Jan
Any way to get to this 60yrs old article any cheaper?
The parameters of nonlinear devices from harmonic measurements - IEEE Journals & Magazine
The parameters of nonlinear devices from harmonic measurements - IEEE Journals & Magazine
Go to the library of a university of technology, if you have one nearby, and make a copy.
The difficult part will be dealing with dynamic (non-instantaneous) effects, apparently you then need Volterra series (which summarizes all I know about Volterra series). Maybe in the middle of the passband you can still gain something by treating everything as instantaneous.
The difficult part will be dealing with dynamic (non-instantaneous) effects, apparently you then need Volterra series (which summarizes all I know about Volterra series). Maybe in the middle of the passband you can still gain something by treating everything as instantaneous.
Last edited:
For now I am really interested only in the instantaneous compensation - basically fixing the non-linear gain in DA/AD and in the analog filters of the soundcard. Volterra series are way way above my skills 🙂
I will ask at the library of our local university but doubt they will have this 60 years old US journal. Or I will bite the bullet and cough up those 33 bucks...
I will ask at the library of our local university but doubt they will have this 60 years old US journal. Or I will bite the bullet and cough up those 33 bucks...
> library of our local university but doubt they will have this 60 years old US journal.
Of course not BUT they may have access for research purposes. Get a log-on for their PCs, go to the IEEE site at that link, but now when you click "PDF" you don't get "Member or Institutional Sign In", the PDF comes right up. (Be prepared with a thumb-drive to Save and coins to Print.) (Depending on bureaucracy, you might instead have to ask librarian for a special sign-in; or the library may not be able to justify IEEE access if their EE program or their budget is weak.)
Don't coff-up 33 bucks yet. Copying an IEEE paper for a friend is not kosher, but someone might email it to you. (Sadly not me.... my IEEE access through ex-school is fading.)
Of course not BUT they may have access for research purposes. Get a log-on for their PCs, go to the IEEE site at that link, but now when you click "PDF" you don't get "Member or Institutional Sign In", the PDF comes right up. (Be prepared with a thumb-drive to Save and coins to Print.) (Depending on bureaucracy, you might instead have to ask librarian for a special sign-in; or the library may not be able to justify IEEE access if their EE program or their budget is weak.)
Don't coff-up 33 bucks yet. Copying an IEEE paper for a friend is not kosher, but someone might email it to you. (Sadly not me.... my IEEE access through ex-school is fading.)
> our local university
Západočeská Univerzita v Plzni? Gosh, it is amazing how much that campus looks like the US school I worked for. (I think they all use the same plan-books and the same photographers..)
ZČU is certainly big enough, and has a strong EE program.
And look near the bottom of this page:
Univerzitni knihovna - Databaze
"IEEE Xplore, ACM Digital Library"
I bet if you are ON campus, or maybe IN library, that link will open full access to IEEE archives. (For a while I could access from 500 miles off campus by authenticating to an on-campus proxy, but it broke.)
Západočeská Univerzita v Plzni? Gosh, it is amazing how much that campus looks like the US school I worked for. (I think they all use the same plan-books and the same photographers..)
ZČU is certainly big enough, and has a strong EE program.
And look near the bottom of this page:
Univerzitni knihovna - Databaze
"IEEE Xplore, ACM Digital Library"
I bet if you are ON campus, or maybe IN library, that link will open full access to IEEE archives. (For a while I could access from 500 miles off campus by authenticating to an on-campus proxy, but it broke.)
Its not a single compensation. You have source nonlinearities and ADC nonlinearities. Further they are not monotonic and change with level as well as frequency. From what I have seen if the distortions are simple (simple curve in the transfer) and in the .1% range it may be possible. At the -100 dB or less the distortions often have broad harmonic content which suggests more abrupt nonlinearities.
On the DACs the distortion cancelling is something of a standard thing (both TI and AKM have mentioned it to me) and its based on an understanding of the internal structure of the chip. I'm not sure if you can extend it much further than they already have.
On the DACs the distortion cancelling is something of a standard thing (both TI and AKM have mentioned it to me) and its based on an understanding of the internal structure of the chip. I'm not sure if you can extend it much further than they already have.
All I want to try is calculating e.g. 4th order transfer polynom for the whole loop based on 4 measured harmonics and see what it does. ESS does something in their ES9028/38 line - the datasheet defines a register for second and third harmonic reduction. I know there is no scope for a major improvement.
I want to test it in python, with pre-recorded data. If it does not work - even that would be a result to learn from .
I want to test it in python, with pre-recorded data. If it does not work - even that would be a result to learn from .
PRR: Thanks a lot for your hint. I asked my friend at the university math department. He will try to get it, hopefully the library has subscribed to this historic IEEE section.
> my friend at the university math department
Excellent. In his office, old IEEE papers probably pop right up. I believe IEEE typically licenses the full archive to the full university network. If not whole-campus, your friend surely knows how to get math papers, and the same should work for IEEE.
Excellent. In his office, old IEEE papers probably pop right up. I believe IEEE typically licenses the full archive to the full university network. If not whole-campus, your friend surely knows how to get math papers, and the same should work for IEEE.
For low-order harmonic distortion you can distinguish between the DAC and the ADC by measuring with and without an attenuator between DAC and ADC, although loading effects might mess up the results.
I mean, suppose you design a practically distortion-free resistor network that has two attenuation settings (0 dB and something else, for example) and that when sourced by the DAC and loaded by the ADC has input and output impedances that are independent of the attenuation settings. Suppose the Taylor series that describe the DAC's and ADC's non-linearity have no terms above the third. The n-th harmonic with n = 2 or 3 is then proportional to the n-th power of the signal level, while the n-th harmonic distortion is almost proportional to the n-1st power, because it is normalized to the fundamental. Hence, the ADC's distortion changes when the attenuation is switched, while the DAC's doesn't.
I wrote "almost" because the third-order term in the Taylor series also changes the fundamental level a bit. For fourth and higher order, things get more complicated because the fourth-order term also causes second-harmonic distortion.
I mean, suppose you design a practically distortion-free resistor network that has two attenuation settings (0 dB and something else, for example) and that when sourced by the DAC and loaded by the ADC has input and output impedances that are independent of the attenuation settings. Suppose the Taylor series that describe the DAC's and ADC's non-linearity have no terms above the third. The n-th harmonic with n = 2 or 3 is then proportional to the n-th power of the signal level, while the n-th harmonic distortion is almost proportional to the n-1st power, because it is normalized to the fundamental. Hence, the ADC's distortion changes when the attenuation is switched, while the DAC's doesn't.
I wrote "almost" because the third-order term in the Taylor series also changes the fundamental level a bit. For fourth and higher order, things get more complicated because the fourth-order term also causes second-harmonic distortion.
Last edited:
Very interesting. Ideally the goal would be calibrating/compensating both outputs and inputs, not only the overall loop. Your proposal would enable (to some precision, as everything here) to identify these two contributions to the overall loop distortion.
Thanks a lot for your proposal. If the principle with nonlinearities compensation turns out effective/working, this would definitely be the next step.
For my measurement workstation I am planning a PC-controlled calibration circuit (originally only for the virtual balanced configuration), adding a switchable divider into the loop would be simple.
Thanks a lot for your proposal. If the principle with nonlinearities compensation turns out effective/working, this would definitely be the next step.
For my measurement workstation I am planning a PC-controlled calibration circuit (originally only for the virtual balanced configuration), adding a switchable divider into the loop would be simple.
An internal soundcard of a large noisy dual-xeon workstation, stereo loop out -> in with a 2m coiled thinnie.
Measured by Arta running in linux + wine.
The transfer polynomials are configured in a modified alsa route plugin (listed from 0th - 5th order, the plugin supports up to 10 orders):
The coefficients are calculated by a script in Octave.
The principle is actually very simple - the polynomial is calculated as best-fitting transformation from a wave recorded in calibration to a precise sine wave, generated directly in octave. Frequency of the incoming wave is known (since we have both ends of the measurement chain under control), phase shift of the recorded wave is measured with fft (just a few periods of samples produce very precise phase value for the first harmonic). Surprisingly simulations in octave and the actual measured performance are rather coherent.
The calibration holds only for a very limited range of frequencies and amplitude levels. I think that many not be a problem for measurements, it is possible to fully automate the whole process with several signal relays and resistors (my next goal).
All the scripts and route plugin patches will be posted on github within a few days, any improvements/patches/suggestions are very welcome. It will take some time before the scripts get robust enough to allow reliable automated calibration.
I will compile the plugin for my measurement workstation with ESI Juli to test a decent soundcard in a cleaner environment. Simulations in octave with pre-recorded Juli output are positive 🙂
It seems to work 🙂
Measured by Arta running in linux + wine.
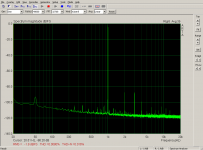
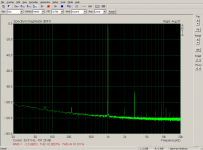
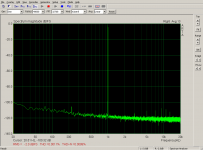
- The first screenshot shows performance of the actual hardware - loop hw out -> hw in.
- The second screenshot is virtual balanced setup made from two channels where each has its DC offset and linear gain calibrated/compensated.
- The third screenshot is virtual balanced setup, each hw channel is compensated with a fifth-order polynomial calculated to cancel out static non-linearities.
The transfer polynomials are configured in a modified alsa route plugin (listed from 0th - 5th order, the plugin supports up to 10 orders):
Code:
pcm.symmetric_in {
type route
slave {
pcm "hw:0"
channels 2
}
ttable {
0.0 { polynom [-3.2787e-05 4.9206e-01 2.5843e-05 1.4382e-04 8.1172e-05 2.0301e-05 ] }
0.1 { polynom [ 6.7723e-06 -4.9254e-01 -1.1393e-06 -1.8654e-04 -9.9866e-05 3.8831e-05 ] }
1.0 { polynom [-3.2787e-05 4.9206e-01 2.5843e-05 1.4382e-04 8.1172e-05 2.0301e-05 ] }
1.1 { polynom [ 6.7723e-06 -4.9254e-01 -1.1393e-06 -1.8654e-04 -9.9866e-05 3.8831e-05 ] }
}
}The coefficients are calculated by a script in Octave.
The principle is actually very simple - the polynomial is calculated as best-fitting transformation from a wave recorded in calibration to a precise sine wave, generated directly in octave. Frequency of the incoming wave is known (since we have both ends of the measurement chain under control), phase shift of the recorded wave is measured with fft (just a few periods of samples produce very precise phase value for the first harmonic). Surprisingly simulations in octave and the actual measured performance are rather coherent.
The calibration holds only for a very limited range of frequencies and amplitude levels. I think that many not be a problem for measurements, it is possible to fully automate the whole process with several signal relays and resistors (my next goal).
All the scripts and route plugin patches will be posted on github within a few days, any improvements/patches/suggestions are very welcome. It will take some time before the scripts get robust enough to allow reliable automated calibration.
I will compile the plugin for my measurement workstation with ESI Juli to test a decent soundcard in a cleaner environment. Simulations in octave with pre-recorded Juli output are positive 🙂
It seems to work 🙂
Attachments
Last edited:
That's impressive. You are running ARTA in Wine? Are you using ASIO or Wine implementation of Windows audio? Is it 24 bit capable? (I have seen complaints elsewhere.) Also impressive is how easy that was to implement in Linux.
Congratulations on your success! 🙂I guess your coefficients are fixed one. Do you have a plan to make them variable? I'm sure If you want more than 120dB SFDR, you need to do some precautions to prevent temperature drift or other disturbance. DSM DAC with internal calibration can have such high SFDR but sometimes fails to have repeatability. The most effective solution for the problem is continuous calibration, where real-time FFT constantly adjust the valuables and keep high SFDR. It may work successfully though I haven't implemented such a system in real PCB. Does your system have the ability of real-time calibration? I think it's the destination to achieve excellent distortion system.
This is incredible! I was very skeptical that it could work at all, but you proved me wrong.
Bad for me, good for you ! ;-)
Jan
Bad for me, good for you ! ;-)
Jan
- Home
- Design & Build
- Equipment & Tools
- Digital Distortion Compensation for Measurement Setup