I understood DF96 talking about the individual properties of cable - and its resulting impedance for a best working transmission line - certainly terminated.
No. See a good text book or Wikipedia. Below a few 10s or 100s of kHz the characteristic impedance of almost any practical transmission line rises and becomes non-resistive. This is because the formula for Z is dominated by R and C - I mean the full formula, not the Z=sqrt(L/C) approximation which is only true for higher frequencies.Mark Tillotson said:
> Wikipedia. Below a few 10s or 100s of kHz the characteristic impedance of almost any practical transmission line rises and becomes non-resistive.
Wikipedia does not help.
VIAS page 12 gives old-old data for telephone lines. Paper insulation! See Table 1. Taking #19 we have 85r and 2uMho (500kOhms) per mile; both increase directly with distance so we use the ratio. Assuming these 1KHz resistances are nearly true at "DC", I get about 6k DC impedance. (With PVC I would expect tens of kOhms.)
Also "NOTE: Inductance is 0.001 henry per loop mile for all gauges." This is not true for all cases, but nearly true for any close-spaced cable.
By 1KHz the notional impedance is 402 Ohms because of all the capacitance.
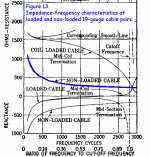
See Fig 13 page 10. Ignore all the "loaded" trickery. A non-loaded cable may be hundreds of Ohms at mid-audio, but is clearly rising to kOhms by around 50Hz. (And I bet it falls to ~~100r by 1MHz-- most twisted-pair does.)
But telephony is/was about miles of cable. When we have just a foot of cable all those reactances matter 5,280 times less. The audio impedance of a foot of cable approaches the "DC" impedance of long cable, typically thousands of Ohms.
Wikipedia does not help.
VIAS page 12 gives old-old data for telephone lines. Paper insulation! See Table 1. Taking #19 we have 85r and 2uMho (500kOhms) per mile; both increase directly with distance so we use the ratio. Assuming these 1KHz resistances are nearly true at "DC", I get about 6k DC impedance. (With PVC I would expect tens of kOhms.)
Also "NOTE: Inductance is 0.001 henry per loop mile for all gauges." This is not true for all cases, but nearly true for any close-spaced cable.
By 1KHz the notional impedance is 402 Ohms because of all the capacitance.
See Fig 13 page 10. Ignore all the "loaded" trickery. A non-loaded cable may be hundreds of Ohms at mid-audio, but is clearly rising to kOhms by around 50Hz. (And I bet it falls to ~~100r by 1MHz-- most twisted-pair does.)
But telephony is/was about miles of cable. When we have just a foot of cable all those reactances matter 5,280 times less. The audio impedance of a foot of cable approaches the "DC" impedance of long cable, typically thousands of Ohms.
Attachments
When the lineic resistance of the line equals its lineic inductive reactance, the LF cutoff frequency of the characteristic impedance is reached, meaning its magnitude increases and its phase resembles that of a RC.
It is the reason why POTS terminating impedances are (more or less complex) RC circuits
Depending on the construction of the line (and mainly the quantity of copper) the cutoff requency can be as high as hundreds of kHz (for cheap cables of asian origin for example), or as low as hundreds of Hz.
It could reach DC, but only for superconductive cables
I am talking about the ideal transmission line approximation, not a kilometre of twisted pair (with associated loss), so the characteristic impedance can be treated as purely resistive. I wouldn't expect to site the turntable and preamp so far apart that the full Heaviside telegrapher's equations apply!
See Transmission line - Wikipedia. This gives the full formula for Z. It is clear that Z is only resistive at very low frequencies (where R and G dominate) and high frequencies (where L and C dominate). In between, including much of the audio band, Z is non-resistive and frequency-dependent. Note too that the DC characteristic impedance and the RF characteristic impedance are extremely unlikely to be similar, let alone identical.PRR said:
True. False. The characteristic impedance of a cable does not depend on length; however, the relevance of characteristic impedance depends on length and becomes irrelevant at very short lengths.
You have superconducting interconnect cables?Mark Tillotson said:
You made a false statement about characteristic impedance (namely, that DC and RF impedances are the same), which I corrected. The context of your remark was a particular real cable, not a hypothetical ideal cable. You can't wriggle out by pretending something different. As I said, the length of the cable is irrelevant: 0.5m of a particular cable has the same characteristic impedance at 1kHz as 5km of that cable; the telegrapher's equation applies fully to both. Whether it is relevant is a separate issue.
You clearly aren't able to use sensible simplifying approximations - for a few feet of twisted pair made out of copper you can treat Z0 as purely resistive and everything works just fine, the few parts per thousand error due to losses is neither here nor there, you can treat the freq response as flat DC to MHz within a tiny fraction of a dB if terminated with Z0. Thats good enough for anyone.
Building an undersea cable, then yes you need the full analysis of telegrapher's equations, skin-effect, dilelectric dependence on frequency and loss tangent. Here that's simply a waste of effort.
At RF transmission lines are modelled as purely resistive with a frequency-dependent loss factor. Nothing more complicated is required.
Building an undersea cable, then yes you need the full analysis of telegrapher's equations, skin-effect, dilelectric dependence on frequency and loss tangent. Here that's simply a waste of effort.
At RF transmission lines are modelled as purely resistive with a frequency-dependent loss factor. Nothing more complicated is required.
You keep changing the subject. Much simpler to just admit that you made a mistake: a cable characteristic impedance is not constant from DC to RF. You seem unable or unwilling to accept the "sensible simplifying approximation" that at audio frequency a cable has Z0=sqrt(R/jwC), which is not resistive and not constant.
That is because at RF that is a good approximation.
No.
No.
I'm not talking about kilometre runs, for a short section the lossless approximation will hold because the load resistor is a few nanoseconds away, so you can treat the impedance as constant from DC upwards (not the case for long cables runs like a telegraph itself).
The cutoff frequency where R starts to matter is w = R/L, perhaps around 30kHz (R = 10 milliohms/metre, L = 50nH/metre).
But for a metre of transmission line at 30kHz is 0.0001 wavelength, so the max error by assuming Z0 is constant is of the order of 100ppm.
The approximation holds just fine, the impedance looking into the short terminated transmission line is constant from DC to GHz to all practical purposes. What's hard to understand about that? Its also very easy to measure!
[ As an afterthought - this ability to treat Z0 as constant from DC up is what 75 ohm video cabling relies on - and yes for very long runs you do have issues there, due to the dispersion and non-flat response, but not for a few metres ]
The cutoff frequency where R starts to matter is w = R/L, perhaps around 30kHz (R = 10 milliohms/metre, L = 50nH/metre).
But for a metre of transmission line at 30kHz is 0.0001 wavelength, so the max error by assuming Z0 is constant is of the order of 100ppm.
The approximation holds just fine, the impedance looking into the short terminated transmission line is constant from DC to GHz to all practical purposes. What's hard to understand about that? Its also very easy to measure!
[ As an afterthought - this ability to treat Z0 as constant from DC up is what 75 ohm video cabling relies on - and yes for very long runs you do have issues there, due to the dispersion and non-flat response, but not for a few metres ]
Last edited:
No. You don't get it, do you? You are wrapping together characteristic impedance and the effect of characteristic impedance and pretending that this is one subject. Video cable works because at low frequencies it is short, not because at low frequencies it is still 75R.
You said that at 100R his cable will match his cartridge. This is simply false. The truth is that at audio frequencies the cable will be nowhere near 100R, so it cannot match his cartridge but this does not matter because the cable is short.
You said that at 100R his cable will match his cartridge. This is simply false. The truth is that at audio frequencies the cable will be nowhere near 100R, so it cannot match his cartridge but this does not matter because the cable is short.
You are once again mixing up two quite different things. At DC the line does very little so you simply see the termination, whatever its value. At GHz you see a matched line. Two quite different effects, but they can be mixed up into one experiment by someone who does not understand what he is doing.Mark Tillotson said:
I understand perfectly - this is what a simplifying assumption is all about, making things easy and simple, which you seem hell-bent to avoid. If I was sending a signal over kilometres of twisted pair I would have to worry about this, and also about the attenuation (which is part and parcel of the breakdown of the lossless approximation at low frequencies and long lines)
If you are sending signals a few metres only, you can assume all terminated transmission lines have constant Z0 from DC to the cutoff frequency, and are lossless at low frequency, and this is assumed widely and relied on in many many disciplines. Losses increase at higher frequencies due to skin effect and imperfect dielectrics, but with minimal disruption to Z0.
You are coming at this from the direction of telecomms perspective, which is different from all the short signal distribution applications.
The breakdown of the lossless assumption happens when the power losses become significant, and at this point the line is no longer a transmission line in the normally accepted sense anyway, as it is dominated by resistance, not wave propagation. For typical audio cables this would happen at lengths of 100's of metres, which is never seen.
If you are sending signals a few metres only, you can assume all terminated transmission lines have constant Z0 from DC to the cutoff frequency, and are lossless at low frequency, and this is assumed widely and relied on in many many disciplines. Losses increase at higher frequencies due to skin effect and imperfect dielectrics, but with minimal disruption to Z0.
You are coming at this from the direction of telecomms perspective, which is different from all the short signal distribution applications.
The breakdown of the lossless assumption happens when the power losses become significant, and at this point the line is no longer a transmission line in the normally accepted sense anyway, as it is dominated by resistance, not wave propagation. For typical audio cables this would happen at lengths of 100's of metres, which is never seen.
I can't speak for what many discipline may or may not assume. However, you continue to mix up two quite different phenomena: the irrelevance of a short line, and the correct termination of a significant line. I am not trying to avoid simplicity, but I am trying to avoid oversimplification. There are lots of engineers who actually believe that the characteristic impedance of a cable is sqrt(L/C) at all frequencies; using a simplified approximation where it is not valid is something they sometimes do. You seem to be encouraging this sort of confusion, however clear things may be to you.Mark Tillotson said:
So can we agree:
1. the characteristic impedance of some twisted wire is not 100 ohms at audio frequency
2. this does not matter if the wire is short
- Status
- Not open for further replies.