I am looking for a way to build a device with a know amount of distortion for testing my HP 339A. Something with 1%, 3% 10% doesn't matter as long as it is a known amount.
How would I do that??
How would I do that??
Hi,
Things like square waves, sawtooth, triangular all have fixed
high levels of distortion, the values I do not know offhand.
But you could simply mix two known signals together
with one representing the distortion could you not ?
🙂/sreten.
Things like square waves, sawtooth, triangular all have fixed
high levels of distortion, the values I do not know offhand.
But you could simply mix two known signals together
with one representing the distortion could you not ?
🙂/sreten.
I made them in Audition (Cooledit) and burned them onto a CD (not these exactly but other test waveforms).
Yeah i have ways to create waveforms including sig gens and soundforge etc, but nothing where i can create a device or a signal with a know about of distortion.
I would like to build a box. some form of op-amp device with a way to create a precise amount of distortion.
Zc
I would like to build a box. some form of op-amp device with a way to create a precise amount of distortion.
Zc
Here is a distortion meter/signal generator. You should be able to create signals with a measured amount of distortion, if only by trial-and-error.
w
You can create a signal with arbitrary distortion characteristics by calculation. Values can be created in Excel, for example, for a pure sampled sine wave, which can have a harmonic added at a lower amplitude. Then the values can be turned into a .wav file and played back. Figuring out how to do this is almost as interesting as playing with opamps.
w
You can create a signal with arbitrary distortion characteristics by calculation. Values can be created in Excel, for example, for a pure sampled sine wave, which can have a harmonic added at a lower amplitude. Then the values can be turned into a .wav file and played back. Figuring out how to do this is almost as interesting as playing with opamps.
The 339 measures always THD+noise and not THD. You can exclude high and low frequency noise with the build in HP & LP filters, but that will not lead to an exact calibration.
The THD level of a squarewave also depends on its exact 50/50 duty cycle and a very fast rise time.
A good & cheap way may be any analyzer-software like Specralab as a reference, but the noise problem is still present.
Hardi
The THD level of a squarewave also depends on its exact 50/50 duty cycle and a very fast rise time.
A good & cheap way may be any analyzer-software like Specralab as a reference, but the noise problem is still present.
Hardi
http://www.diyaudio.com/forums/showthread.php?postid=1178021#post1178021
and others in that thread use LtSpice to create .wav files with known components
and others in that thread use LtSpice to create .wav files with known components
Ideal, jacknnj
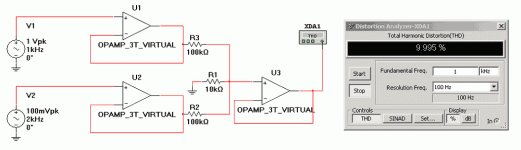
You can send the fundamental out your L channel and the harmonic out the R channel.
However real world distortion is never just in 1 harmonic. But then I guess it's just a ballpark test for a meter.
I'd still just combine the signals somehow in the digital domain, and play the result back thru a single channel of a good DAC. Less hardware, less problems.
w
You can send the fundamental out your L channel and the harmonic out the R channel.
However real world distortion is never just in 1 harmonic. But then I guess it's just a ballpark test for a meter.
I'd still just combine the signals somehow in the digital domain, and play the result back thru a single channel of a good DAC. Less hardware, less problems.
w
Zero Cool said:I am looking for a way to build a device with a know amount of distortion for testing my HP 339A. Something with 1%, 3% 10% doesn't matter as long as it is a known amount.
How would I do that??
If you want to make it in hardware, you can follow the idea of jacknj, but to be more practical, you start with a low distorsion sine wave you split in two: one direct way to the output, and another one through a comparator and calibrated attenuator.
In a squarewave, the distorsion is inversely proportional to the frequency:
-peak value of fundamental is pi/2 times the amplitude
-peak value of third harmonic is a third of above value
-peak value of fifth is a fifth
and so on and so forth
You can easily calculate which proportion of squarewave will give a certain amount of distortion within a certain bandwidth, and for low levels you'll be able to neglect the slight increase in fundamental amplitude.
Plus, you'll get something a bit more realistic than a single harmonic.
You should check the docs on Bob Cordell's site, but to calibrate the Cordell analyzer I think it was simply a matter of setting a certain amplitude of the main signal, then adding in second harmonic via a second signal generator and a large resistor. Seemed reasonably fool proof.
With the expression evaluator of the free Goldwave you can create a .wav file with any arbitrary waveform, like a sine with defined harmonics. Or play it directly through your soundcard.
A 1 kHz sine with one defined harmonic (say the 3rd) should be sufficient to calibrate your distortion analyser, provided the noise floor is low enough.
😉
A 1 kHz sine with one defined harmonic (say the 3rd) should be sufficient to calibrate your distortion analyser, provided the noise floor is low enough.
😉
ahhh now we are getting somewhere. I get it. I didnt understand at first how jacks schematic was working. it's one of those DUh its so simple things!
and the square wave information is great. I will dig into that a bit further as well.
Zc
and the square wave information is great. I will dig into that a bit further as well.
Zc
I have used special waveshapes (square, triangle, sawtooth) to check an HP339A, and I generally get good results, but there are some gotchas to look out for.
If you use a square wave, the instrument must see up to and including the 867th harmonic (without attenuation) in order to get 99.9% accuracy! You won't be able to use a fundamental much higher than, say, 50 Hz or 100 Hz to be sure the 867th harmonic is seen, unattenuated, by the instrument.
If you use a triangle wave, the measurement need only see up to and including the 17th harmonic to get 99.9% accuracy. This is reasonable on the 339A. A 1kHz triangle wave will have a 17th harmonic at 17 kHz, well within the range of the instrument.
The exact THD of a 50% duty factor square wave is 43.5236%. If we say that a triangle wave has a "duty factor" equal to the time of the positive going ramp divided by the total period, then the THD of a 50% "duty factor" triangle wave is 12.0273%.
The THD of both square waves and triangle waves vary with duty factor, reaching a minimum at 50%. Many function generators have a knob to adjust duty factor, and if the duty factor is varied while measuring the THD on the 339A, the minimum will be the theoretical numbers given above (assuming the instrument sees enough harmonics, of course).
One could make a square wave generator with variable duty factor with a 555 timer, and then integrate the square wave with a simple opamp integrator. The sides of the triangle wave must be straight for the given theoretical distortion to be correct, so a simple RC integrator won't suffice; an opamp will be needed.
I've attached a graphic showing the distortion of square waves and triangle waves versus duty factor. Notice that when the "duty factor" of the triangle wave approaches either zero or one, the waveform becomes a sawtooth, with a theoretical distortion of 62.6157%.
In the case of the sawtooth, harmonics up to and including the 943rd must be seen by the instrument (without attenuation) to get 99.9% accuracy.
If you use a square wave, the instrument must see up to and including the 867th harmonic (without attenuation) in order to get 99.9% accuracy! You won't be able to use a fundamental much higher than, say, 50 Hz or 100 Hz to be sure the 867th harmonic is seen, unattenuated, by the instrument.
If you use a triangle wave, the measurement need only see up to and including the 17th harmonic to get 99.9% accuracy. This is reasonable on the 339A. A 1kHz triangle wave will have a 17th harmonic at 17 kHz, well within the range of the instrument.
The exact THD of a 50% duty factor square wave is 43.5236%. If we say that a triangle wave has a "duty factor" equal to the time of the positive going ramp divided by the total period, then the THD of a 50% "duty factor" triangle wave is 12.0273%.
The THD of both square waves and triangle waves vary with duty factor, reaching a minimum at 50%. Many function generators have a knob to adjust duty factor, and if the duty factor is varied while measuring the THD on the 339A, the minimum will be the theoretical numbers given above (assuming the instrument sees enough harmonics, of course).
One could make a square wave generator with variable duty factor with a 555 timer, and then integrate the square wave with a simple opamp integrator. The sides of the triangle wave must be straight for the given theoretical distortion to be correct, so a simple RC integrator won't suffice; an opamp will be needed.
I've attached a graphic showing the distortion of square waves and triangle waves versus duty factor. Notice that when the "duty factor" of the triangle wave approaches either zero or one, the waveform becomes a sawtooth, with a theoretical distortion of 62.6157%.
In the case of the sawtooth, harmonics up to and including the 943rd must be seen by the instrument (without attenuation) to get 99.9% accuracy.
An externally hosted image should be here but it was not working when we last tested it.
Of course, but as I pointed out, you can't expect to get good results with square waves having a fundamental much greater than 50 Hz. In that case, if the rise and fall times are not more than 1 microsecond, the measured distortion will not be affected by the rise and fall times.
Rise times on the order of 1 microsecond are trivially easy to generate nowadays, but certainly a person should verify it before using such a waveform to check calibration of a 339A. The commercial function generators I've used had rise times well under a microsecond.
A CMOS 555 timer circuit will easily do better than a microsecond. The one I have on my bench generates a square wave with a rise time of 27 nS and a fall time of 12 nS.
Another perturbation which will affect the distortion is non-flatness of the top and bottom of the square wave, sometimes called tilt or droop. These perturbations will lead to non-straight ramps if used to generate a triangle wave by integration, an undesirable defect I mentioned in the previous post.
The previous post assumed ideal waveforms, except for duty factor variations. The user will have to beware of other non-idealities.
Rise times on the order of 1 microsecond are trivially easy to generate nowadays, but certainly a person should verify it before using such a waveform to check calibration of a 339A. The commercial function generators I've used had rise times well under a microsecond.
A CMOS 555 timer circuit will easily do better than a microsecond. The one I have on my bench generates a square wave with a rise time of 27 nS and a fall time of 12 nS.
Another perturbation which will affect the distortion is non-flatness of the top and bottom of the square wave, sometimes called tilt or droop. These perturbations will lead to non-straight ramps if used to generate a triangle wave by integration, an undesirable defect I mentioned in the previous post.
The previous post assumed ideal waveforms, except for duty factor variations. The user will have to beware of other non-idealities.
A good idea may be a true rms millivoltmeter as reference to measure the components after the 339 notch filter. You can calculate the THD+N percentage with the knowledge of the rms value of the THD+N components (behind the notch) and the rms value of the input signal.
Before this is done, i would calibrate the notch for highest damping as discribed in the manual.
Before this is done, i would calibrate the notch for highest damping as discribed in the manual.
Hmm, I see a lot of hardware solutions. But what’s wrong by using a soundcard for the source? Most good soundcards have distortion figures comparable to the measurement floor of the HP 339A nowadays.
You can start with a pure sine at say minus 6-10 dB to see what is the residual distortion. And after that, ad harmonics at wish.
Cheers 😉
You can start with a pure sine at say minus 6-10 dB to see what is the residual distortion. And after that, ad harmonics at wish.
Cheers 😉
Some soundcards are too noisy while having a clean THD spectrum up zo 20 KHZ. There can be aliasing noise or low frequency hum....Also with some "good" cards.
The 339 measures everything (hum + noise) up to 110 KHz!
It´s also a good idea to use the HP339s 30 KHz filter in this case.
The 339 measures everything (hum + noise) up to 110 KHz!
It´s also a good idea to use the HP339s 30 KHz filter in this case.
- Status
- Not open for further replies.
- Home
- Design & Build
- Equipment & Tools
- Calibrated distortion source???