BudP said:
And you know this how? I hope that you don't just listen and draw this conclusion.
Earl
CUTE TRICKs
Hi
Lynn. I am sure your cute trick works for OB's just the same as for cabinets.
What you hear pressing your ear to the baffle ( is it for a box or OB ) is the resonant properties of that material – Size, stiffness and inner damping.
http://youtube.com/watch?v=Zkox6niJ1Wc
" http://youtube.com/watch?v=Zkox6niJ1Wc"
Overlayed is HOW and to what extent this resonances are stimulated.
Pressure difference is basically the same for boxed and OB baffles and standing waves inside boxes have sort of equivalent in room modes that for sure will stimulate OB movement more than movement of boxes ( especially in the size you are aiming to ). One - mostly overlooked - stimulus is also the reactive force of membrane acceleration.
Here is another "cute trick" I discovered accidentally that fits nicely to the above.
Take a sheet of paper - bend it slightly to stiffen it and hold it upwards with one hand while listening to music ( pretend following the score if someone watches you... 😀 ).
Even at moderate listening levels you will notice that sheet of paper vibrating between your fingers.
What makes it a "cute trick" is my very subjective observation that the strength of the haptic sense in my fingers correlate to some extend with the quality ( NOT quantity ) of bass performance of my speakers alignment.
I speculate that this is due to the fact that ALL the body becomes sensitive to sound as frequency drops and there seems to be sort of coherence between "body hearing" and "ear hearing" that works out better or worse.
Congratulations – good start.
It took me ONE year to walk fairly straight on after a knee injury from skiing as a young boy. I discovered as recently as two years ago that I have a pattern to still protect that very leg unconscious under some circumstances.
Greetings
Michael
Hi
Lynn. I am sure your cute trick works for OB's just the same as for cabinets.
What you hear pressing your ear to the baffle ( is it for a box or OB ) is the resonant properties of that material – Size, stiffness and inner damping.
http://youtube.com/watch?v=Zkox6niJ1Wc
" http://youtube.com/watch?v=Zkox6niJ1Wc"
Overlayed is HOW and to what extent this resonances are stimulated.
Pressure difference is basically the same for boxed and OB baffles and standing waves inside boxes have sort of equivalent in room modes that for sure will stimulate OB movement more than movement of boxes ( especially in the size you are aiming to ). One - mostly overlooked - stimulus is also the reactive force of membrane acceleration.
Here is another "cute trick" I discovered accidentally that fits nicely to the above.
Take a sheet of paper - bend it slightly to stiffen it and hold it upwards with one hand while listening to music ( pretend following the score if someone watches you... 😀 ).
Even at moderate listening levels you will notice that sheet of paper vibrating between your fingers.
What makes it a "cute trick" is my very subjective observation that the strength of the haptic sense in my fingers correlate to some extend with the quality ( NOT quantity ) of bass performance of my speakers alignment.
I speculate that this is due to the fact that ALL the body becomes sensitive to sound as frequency drops and there seems to be sort of coherence between "body hearing" and "ear hearing" that works out better or worse.
Congratulations – good start.
It took me ONE year to walk fairly straight on after a knee injury from skiing as a young boy. I discovered as recently as two years ago that I have a pattern to still protect that very leg unconscious under some circumstances.
Greetings
Michael
john k... said:
john k.
I still can´t follow your presumption, that zero edge thickness eliminates diffraction in a dipole OB. If the baffle step in a conventional speaker is a diffraction effect, an ideal bipole speaker with zero edge thickness should be free of any diffraction, because there is no pressure difference between front and back - regardless of frequency and driver-to-baffle-edge distance.
Plain logic would suggest that in the transition from bipole (two drivers in phase) over closed box (one driver) to dipole (two drivers 180° out of phase) the dipole diffraction should be almost twice that of a CB. I can´t believe that diffraction wise dipole and bipole could act identical.
Rudolf
Rudolf said:
Your analysis here is quite correct and agrees with the software simulations. An OB has at least double the diffraction of a closed baffle. That is the main concern that I have for OB as diffraction is a significant audible effect. The claim of symmetry cancellation is wholey incorrect.
I do object to calling "the baffle step" diffraction, maybe its symantics, but the diffraction is the sound radiated from the edge not the whole field. One could say, loosely, that the "baffle step" results from the combination of the direct sound and the baffle diffraction, but even this is not entirely true as there are other things involved.
I am always conerned about the use of the phrase "baffle step". There is a gain to be had from a baffle, but the effect is highly dependent on almost every variable envolved in the system design - baffle size, total enclosure size, woofer size relative to enclosure size, etc. To me the only way to account for all of this is to actually measure the system in its intended enclosure and to design the crossovers to those measurements. Otherwise you are only guessing at what effect the "baffle step" has on the system.
gedlee said:
Hi Earl,
John has a rather unique method called wave flow visualization
which I must admit, would be much more economical than the typical hardware/software approach.
cheers,
AJ
gedlee said:
Actually the claim of symmetry is correct. Consider this image:
An externally hosted image should be here but it was not working when we last tested it.
It shows a flat baffle dipole system with baffle thickness T. A plane of symmetry passes through the baffle. I would expect that if T becomes very large you can appreciate that this would represent two conventional speakers back to back but operating out of phase. As T gets very large, the strength of the rear sources relative to the back goes as 20 Log(1/T). So as T gets very large, the front and rear responses become independent of each other. However, regardless of the value of T, the mathematical problem remains the same.
Given that the radiation form the front and rear sources is identical in amplitude but inverted in phase, there will be diffraction at the baffle edges as indicated (there will also be secondary diffraction as the wave from the front diffraction edge expands and encounters the back edge, and vise versa, and so on at infinitum, but it is not necessary to consider them to obtain the correct result). If the edge treatment is the same, front and rear, the diffraction of the front and rear wave will also be the same, but opposite in phase.
We know that for a dipole the response at 90 degrees off axis, any where in the symmetry plane, is null. We can measure it! Since the waves from the main sources are identical in amplitude, but 180 degrees out of phase, they must cancel at 90 degrees off axis because there is no difference in their propagation distances to the observation point. Thus, the ONLY way there can be a null at 90 degrees is for the diffraction sources to be of equal amplitude and opposite in phase as well. An obvious requirement since the baffle is split a mathematical plane of symmetry and the font and rear response are inverted images of each other.
It matters not what the strength of the individual diffraction sources is. Since the diffraction source are of equal strength but opposite phase and separated by a distance T they will form a secondary dipole with axis aligned with the primary dipole) which is 20 Log(T/(R+T) below the primary dipole (here I assume a circular baffle of radius R for simplicity). As T goes to zero the, the differential phase difference with position goes to zero and the diffraction sources at 180 degrees out of phase everywhere. As T goes to infinity the front and rear responses become independent of each other and we recoved the solution for a conventional speaker.
john k,
complete cancellation in the baffle plane has never been questioned.
But what about diffraction results in the listening axis? In his explanation of OB diffraction SL comes to the conclusion:
"You might say this is a much stronger diffraction effect than for the closed box - and you are correct - but it is also the characteristic response of an open baffle, dipole source - after equalization."
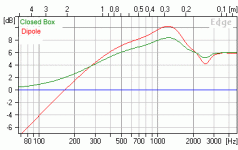
May be it´s just a matter of different naming. So would you call the simulated SPL differences (see diagram) between an open baffle (red) and a closed box baffle of the same size (green) as diffraction effects? Or what else?
And what about the obvious contradiction between dipole and bipole reaction? If opposite phase in front and rear lead to perfect cancellation of diffraction, shouldn´t equal phase in front and rear lead to maximal diffraction?
Rudolf
complete cancellation in the baffle plane has never been questioned.
But what about diffraction results in the listening axis? In his explanation of OB diffraction SL comes to the conclusion:
"You might say this is a much stronger diffraction effect than for the closed box - and you are correct - but it is also the characteristic response of an open baffle, dipole source - after equalization."
May be it´s just a matter of different naming. So would you call the simulated SPL differences (see diagram) between an open baffle (red) and a closed box baffle of the same size (green) as diffraction effects? Or what else?
And what about the obvious contradiction between dipole and bipole reaction? If opposite phase in front and rear lead to perfect cancellation of diffraction, shouldn´t equal phase in front and rear lead to maximal diffraction?
Rudolf
Attachments
Yay! I'm not alone after all. I think Rudolf nailed it, and Dr. Geddes agrees. It's a bipole on an infinitely thin baffle that wouldn't have edge diffraction, just like it doesn't have baffle step losses. The null at the sides of a dipole is a different issue, resulting from 2 out of phase waves travelling the same distance in the same direction, so they net to 0. Edge diffraction is another sound source. Does a rarefaction come rushing around the edge of the baffle to create a sound? Of course not. With a dipole on an infinitely thin baffle there's just one new sound source at the edge, not 2 that net to zero, and it is greater than with a box because the pressure change is greater. I believe it's one of the main causes of imaging problems with OB's, and until diffraction is adequately in OB design they will never reach their maximum sonic potential.
AJ,
Earl was referring to something Bud said, not something I said. BTW my methods must have some validity because they keep coming up with the right answer. You'll get your measurements some day. I just haven't gotten around to it, because it will take a lot of work due to the many things I want to measure.
Earl,
I wish I had the opportunity to take one of your classes, because you and I seem to be on the same wavelength which would really speed up my learning process.
AJ,
Earl was referring to something Bud said, not something I said. BTW my methods must have some validity because they keep coming up with the right answer. You'll get your measurements some day. I just haven't gotten around to it, because it will take a lot of work due to the many things I want to measure.
Earl,
I wish I had the opportunity to take one of your classes, because you and I seem to be on the same wavelength which would really speed up my learning process.
Rudolf said:
I have to run out but I'll have more comments later. Basically SL is just making a comparison between the two observed response curves. It is not possible to separate out diffraction fromt dipole summation (or bipole sumation) from looking at the frequency reponse. The Edge and any baffle sim code, mine too, yield the result of the summation of the primary waves and the diffraction sources from around the baffle edge. Looking at what they yield doesn't necessarily identify diffraction.
I wonder if diffraction simulation assumes incompressible or compressible median. In purely vector based simulation, and thus the results will differ from that of a compressible median.
Re: Re: Re: SL: "Much is hypothesized, little is proven and much is overrated when it comes to
Hi Earl,
I’d like to see how the discussion ends. John k presents a pretty compelling case.
When I left the audio industry, I lost access to an anechoic chamber. That was my impetus to investigate diffraction modeling programs. Not wishing to spend thousands or learn new cumbersome programs, I first considered two freeware tools, The EDGE and The BDS. Not willing to accept their accuracy at face value, I investigated their performance.
As luck would have it, a Lab tech at Seas (Bjorn) was posting a large number of anechoic chamber measures of their drivers, both on IEC baffle, and in a box of very prescribed and known geometry. Bjorn also supplied the measurement particulars (mic position/distance, box angle etc). I can’t recall if he measured two drivers at once in box (woofer and tweeter) to speed things along, I would have to search my notes.
Taking the IEC data, the baffle diffraction was computed with the tool, then “removed” to arrive at a mythical raw driver response. The baffle diffraction was then computed for the speaker in box and added in to this mythical raw driver. The result was compared to the in box measure to arrive at the error curves shown. Opposite errors would cancel, like errors add.
Again, the point of the exercise was to determine the utility of the freeware tools, not make any grand statements and conclusions regarding the general nature of diffraction.
This method is acceptable under the assumption that it’s a linear system and the diffraction effect is min phase. We discussed the min phase assumption at length in the past, your position being that it isn’t. I and a colleague mathematically and empirically substantiated our position, but we didn’t receive a rebuttal with proof. So, the assumption stands unless proven (not stated) otherwise.
BTW, I’m very familiar with your paper, having read it 20 years ago, along with those from John V and all the others. All really good contributions to the art. However, if I recall no real significant consensus was reached at that time on a mathematical model for diffraction, which was supported by empirical evidence. Has the landscape changed? Is there now consensus, supported by empirical evidence? Is there a reference describing it?
Cheers,
Dave
gedlee said:
Hi Earl,
I’d like to see how the discussion ends. John k presents a pretty compelling case.
When I left the audio industry, I lost access to an anechoic chamber. That was my impetus to investigate diffraction modeling programs. Not wishing to spend thousands or learn new cumbersome programs, I first considered two freeware tools, The EDGE and The BDS. Not willing to accept their accuracy at face value, I investigated their performance.
As luck would have it, a Lab tech at Seas (Bjorn) was posting a large number of anechoic chamber measures of their drivers, both on IEC baffle, and in a box of very prescribed and known geometry. Bjorn also supplied the measurement particulars (mic position/distance, box angle etc). I can’t recall if he measured two drivers at once in box (woofer and tweeter) to speed things along, I would have to search my notes.
Taking the IEC data, the baffle diffraction was computed with the tool, then “removed” to arrive at a mythical raw driver response. The baffle diffraction was then computed for the speaker in box and added in to this mythical raw driver. The result was compared to the in box measure to arrive at the error curves shown. Opposite errors would cancel, like errors add.
Again, the point of the exercise was to determine the utility of the freeware tools, not make any grand statements and conclusions regarding the general nature of diffraction.
This method is acceptable under the assumption that it’s a linear system and the diffraction effect is min phase. We discussed the min phase assumption at length in the past, your position being that it isn’t. I and a colleague mathematically and empirically substantiated our position, but we didn’t receive a rebuttal with proof. So, the assumption stands unless proven (not stated) otherwise.
BTW, I’m very familiar with your paper, having read it 20 years ago, along with those from John V and all the others. All really good contributions to the art. However, if I recall no real significant consensus was reached at that time on a mathematical model for diffraction, which was supported by empirical evidence. Has the landscape changed? Is there now consensus, supported by empirical evidence? Is there a reference describing it?
Cheers,
Dave
Hi
from my understanding about diffraction there is nothing to diffract if there is no additional space as the wave propagates.
This should be true for any surface boundary as well as for two absolute identical waves merging at no angel = infinite thin baffle and bipolar operation. Basically the same thing as if we divide an ommni with a ultra thin baffle which also shouldn't create any effects at all (as rudolf already pointed out).
On the other side if we have any other than bipolar operation than with a ultra thin baffle the diffraction creates a second source radiating omnidirectional. As the baffle gets some thickness than there is a secondary dipole established.
IF above holds true than a knifelike baffle edge would fill the 90 degree null with its omnidirectional SPL ( on the formula given by John ) even with true dipole operation.
Anybody out there with a bread slicer who can mount a speaker into and give it quick and dirty measurement?
😀
Greetings
Michael
from my understanding about diffraction there is nothing to diffract if there is no additional space as the wave propagates.
This should be true for any surface boundary as well as for two absolute identical waves merging at no angel = infinite thin baffle and bipolar operation. Basically the same thing as if we divide an ommni with a ultra thin baffle which also shouldn't create any effects at all (as rudolf already pointed out).
On the other side if we have any other than bipolar operation than with a ultra thin baffle the diffraction creates a second source radiating omnidirectional. As the baffle gets some thickness than there is a secondary dipole established.
IF above holds true than a knifelike baffle edge would fill the 90 degree null with its omnidirectional SPL ( on the formula given by John ) even with true dipole operation.
Anybody out there with a bread slicer who can mount a speaker into and give it quick and dirty measurement?
😀
Greetings
Michael
Here are some sims that break out the primary and secondary dipoles for a circular bafle or 6" radius and baffle thicknesses of 2", 0.5" and 0.1" The first set if for non directional sources (point sources). The red traces at the basic primary dipole, blue is the secondary dipole and green is the net response.
T = 2"
T = 0.5"
T = 0.1"
Same thing but with a curde directionality model:
T = 2"
T = 0.5"
T = 0.1"
Note that a directionaly does not mean asymmetry in the source response. It means that the on axis response of the source is different than the 90 degree off axis response. The primary dipole is the sum of the front on axis response and the 90 degree off axis response for the rerar as that is what "leaks" around the baffle. The diffration sources are based on the 90 degree off axis response as that if what propagates to the baffle edge.
As both situations show, (non directioanl and directional) as the baffle thickness goes to zero the diffraction cancels and all that remains is the primary dipole response, as if two omnidirecional, point sources were suspended in space 6" in space w/o a baffle.
That's it for me. You can reach your own conclusions.
T = 2"
An externally hosted image should be here but it was not working when we last tested it.
T = 0.5"
An externally hosted image should be here but it was not working when we last tested it.
T = 0.1"
An externally hosted image should be here but it was not working when we last tested it.
Same thing but with a curde directionality model:
T = 2"
An externally hosted image should be here but it was not working when we last tested it.
T = 0.5"
An externally hosted image should be here but it was not working when we last tested it.
T = 0.1"
An externally hosted image should be here but it was not working when we last tested it.
Note that a directionaly does not mean asymmetry in the source response. It means that the on axis response of the source is different than the 90 degree off axis response. The primary dipole is the sum of the front on axis response and the 90 degree off axis response for the rerar as that is what "leaks" around the baffle. The diffration sources are based on the 90 degree off axis response as that if what propagates to the baffle edge.
As both situations show, (non directioanl and directional) as the baffle thickness goes to zero the diffraction cancels and all that remains is the primary dipole response, as if two omnidirecional, point sources were suspended in space 6" in space w/o a baffle.
That's it for me. You can reach your own conclusions.
john k... said:
Are you guys all missing this? This is the elegant nonmathematical solution to the question of what the essence of the diffraction signature would be. Just a secondary dipole radiator. This answers not only what happens as T=0, and at 90 degrees, but the more general case.
Am I missing something? The symmetry arguement appears quite powerful here. No one has pointed out a flaw in this line of reasoning. John appears quite right. Unless someone can point out a flaw in the above.
ucla88 said:
Appearing right and being right are completely different things. The simulations shown earlier in this thread clearly show that an OB has a greater diffraction effect than a closed box with the edges in the same place. Go back and look at that data.
The reality is that the symmetry argument fails as the baffle becomes thinner because the secondary diffraction effects - off the opposite edges, grow and become comparable to the initial diffraction. Johns argument is valid in the limit as the baffle thickness grows, but it fails in the limit as the baffle thickness goes to zero.
The edges in the zero thickness case are dipole diffractions while they are monopoles diffractions in the finite thickness case. The two solutions do not colapse down to each other in the limit as the baffle thickness disappears.
All empirical evidence also agrees with this position.
"You can draw your own conclusions."
Re: Re: Re: Re: SL: "Much is hypothesized, little is proven and much is overrated when it comes
As I recal we both wrote off the others "proof" as invalid. I presented one also if you recal. You guys never convinced me of your position and when the discussion degenerated into an insulting array of attacks I simply left. As I recal your were one of the decent contributors, too bad about the others guiys as the discussion was never completed.
I still stand by my position that the diffraction is nonminimum phase, or at least this concept does not apply.
I point out, again, the fact that as evidenced by the equations of sound radiation the amplitude of the field changes with position while the phase remains constant (there is no phase term with angle, only radius, while there is an amplitude term in the angle). How could this be minimum phase?
As I have thought about this over the years, it appears to me that the concept of minimum phase may not be applicable to a three dimensional acoustic field. Minimum phase is, after all, an electrical two port concept and one would need to prove that such a concept is still valid for a "field" which cannot be represented as a two port.
To me the fact is simply this, the diffraction portion of the sound field arrives later than the direct sound. This is the part that is subjectively important. To me, The rest of this discussion is academic. It appears to me to be wrong in a lot of aspects, but it is simply not interesting enough (to me) to pursue it any further. I would like to point out that simply having a good argument does not a proof make.
DDF said:
As I recal we both wrote off the others "proof" as invalid. I presented one also if you recal. You guys never convinced me of your position and when the discussion degenerated into an insulting array of attacks I simply left. As I recal your were one of the decent contributors, too bad about the others guiys as the discussion was never completed.
I still stand by my position that the diffraction is nonminimum phase, or at least this concept does not apply.
I point out, again, the fact that as evidenced by the equations of sound radiation the amplitude of the field changes with position while the phase remains constant (there is no phase term with angle, only radius, while there is an amplitude term in the angle). How could this be minimum phase?
As I have thought about this over the years, it appears to me that the concept of minimum phase may not be applicable to a three dimensional acoustic field. Minimum phase is, after all, an electrical two port concept and one would need to prove that such a concept is still valid for a "field" which cannot be represented as a two port.
To me the fact is simply this, the diffraction portion of the sound field arrives later than the direct sound. This is the part that is subjectively important. To me, The rest of this discussion is academic. It appears to me to be wrong in a lot of aspects, but it is simply not interesting enough (to me) to pursue it any further. I would like to point out that simply having a good argument does not a proof make.
I challenge all the believers in computer simulations verses the real world to a simple test. Take any relatively thin baffled dipole. A raw driver will suffice. Start playing some music through it at a reasonable SPL and hold a small piece of paper very near the edge parallel to the plane of the baffle right where the null should be greatest, and where the computer says should net to zero. You'll feel the forces at play acting on the paper. Then come back and try to say that this energy nets to zero, or what is there is so low in magnitude that it shouldn't be addressed.
For those who think this has something to do with asymmetry, just play content you know is low enough in frequency to have symmetry.
A real world experiment is worth several thousand simulations when the programming is flawed. 😀
For those who think this has something to do with asymmetry, just play content you know is low enough in frequency to have symmetry.
A real world experiment is worth several thousand simulations when the programming is flawed. 😀
johninCR said:
Of course it will ! Your paper just become an extension of the baffle itself. It has to deal with two waves of opposite phase and as it is not infinitely (or even reasonably) stiff, it will be moved around.
In other words, your experiment is flawed. Thus your conclusion is flawed too.