Lush and clean isn't an oxymoron? I mean, I play some instruments, and I have recorded a number of instruments, and most of them do not sound lush exactly. Some sound very brash, at least close up. Of course a concert hall and some distance can make up for a lot. The trend in more recent years, however, seems to be for more close micing, as many audiophiles want to hear more 'details.'
Also, muddy doesn't have to come from the power amp. Even something like 'veiled' can come from the AC line ground. Then there is the other equipment in the reproduction chain... You know.
Also, muddy doesn't have to come from the power amp. Even something like 'veiled' can come from the AC line ground. Then there is the other equipment in the reproduction chain... You know.
Last edited:
It may be oxymoron, but that is the best way i can describe it.
Just like every violin has a sound, or acoustic guitar, or piano, each has certain tone.
Tone is its unique harmonic profile.
There is more to sound than thd figure.
You can have clean pre and clean amp, and result will be dry, uninspiring, fatiguing sound.
Just like every violin has a sound, or acoustic guitar, or piano, each has certain tone.
Tone is its unique harmonic profile.
There is more to sound than thd figure.
You can have clean pre and clean amp, and result will be dry, uninspiring, fatiguing sound.
True. Ever wonder why? Its probably reasonable to observe that some it has been explained by Bonsai and others: The low distortion and other measurements fixation by which people may judge designs. IOW, you get what you measure. And they expect good measurements over at ASR.
Thus, that higher distortion designs sound better to you may in some part be an indication that other aspects of good sound were favored over getting the lowest possible distortion. In that case it doesn't mean you especially like distortion. To some extent or other it may mean you just like the focus on other things besides distortion. That said, maybe you like some euphonic distortion too. What do you think it is? Do you think wavebourn was right?
Last edited:
There should be other scoring criteria: degree of boringness, flatness, blandness, flavorlessness.
A friend of mine uses a simplified scale. One of his tests is how long can I listen to this device before I feel like I want to go do something else? Multiple sessions are held on different days where there is time to listen to music for an extended period. The longer on average that the device captures a listener's attention the better on that one particular rating. There are other factors too, maybe even some FFT stuff. Once he is satisfied then he sends out a few units to trusted listeners for their comments, which is another test.
That's one reason i do not like quick AB swapping comparison. I listen to the amp for few days with all sorts of music. Then for another few days with another amp. No memory needed, after few days it gets easy to decide which is more 'musical'. That is more enjoyable. But that's just me.
Don't get me started on double blind stuff. Where suddently you the listener are under stress testing yourself if you remember how what sounded. Utter nonsense.
Don't get me started on double blind stuff. Where suddently you the listener are under stress testing yourself if you remember how what sounded. Utter nonsense.
Regarding test #2 for capacitive loads:
1: You will not catch all unstable amplifiers because the 2ohm load across the capacitors improves phase margin. More realistic would be to put an inductor in series with the resistor.
2: You will not catch all oscillations unless you take it all the way to the rails, because of transistor capacitances and quasi-saturation.
3: A 1us square wave test to the rails with 2.2uF could draw HUNDREDS of amps. Luckily however, this is very unrealistic.
4: All capacitors connected to a voltage drive amplifier with finitesimal output inductance will ring. The presence of this ringing does not in itself mean anything about the stability of the amplifier. If we rate amplifiers higher which ring less, then we are imposing a demand on designers to think up output zobel schemes that have no role in preventing a malfunction. If you think about it, parallel capacitors in a crossover will ring too, it is no different than a capacitor on the output of a stable amplifier. A very long decay of ringing suggests phase margin is low, but the capacitive load test to the rails is a better way to quantify this.
In the load testing post I lost, for an 8ohm amp I suggested a 5.4ohm+27mH load to be tested at full power and beyond at 40Hz. This gives plenty of time for oscillation to emerge. This is a very brutal test and can be done along with the capacitive load test, but I would not make this test last any longer than necessary if I didn't know the amplifier was well derated.
1: You will not catch all unstable amplifiers because the 2ohm load across the capacitors improves phase margin. More realistic would be to put an inductor in series with the resistor.
2: You will not catch all oscillations unless you take it all the way to the rails, because of transistor capacitances and quasi-saturation.
3: A 1us square wave test to the rails with 2.2uF could draw HUNDREDS of amps. Luckily however, this is very unrealistic.
4: All capacitors connected to a voltage drive amplifier with finitesimal output inductance will ring. The presence of this ringing does not in itself mean anything about the stability of the amplifier. If we rate amplifiers higher which ring less, then we are imposing a demand on designers to think up output zobel schemes that have no role in preventing a malfunction. If you think about it, parallel capacitors in a crossover will ring too, it is no different than a capacitor on the output of a stable amplifier. A very long decay of ringing suggests phase margin is low, but the capacitive load test to the rails is a better way to quantify this.
In the load testing post I lost, for an 8ohm amp I suggested a 5.4ohm+27mH load to be tested at full power and beyond at 40Hz. This gives plenty of time for oscillation to emerge. This is a very brutal test and can be done along with the capacitive load test, but I would not make this test last any longer than necessary if I didn't know the amplifier was well derated.
Last edited:
You have described a typical sighted test scenario with full space for imagination and bias. If we want to make scientific criteria of component quality we must use scientific methods of subjective evaluation as well. Subjective output of the test as you have described might be useful only for the person that made the test and cannot be generalized.
To the best of my knowledge, the sine waves used in multitone distortion tests have finite RMS values. Hence, their mean-square values are also finite. I think the assumption of uniformly distributed random phase is enough to ensure ergodicity, so then the variance is equal to the mean-square value and is therefore also finite.
What I'm not so sure about, is whether the random phase assumption is applicable to the multitone tests that are in fashion. It shouldn't matter much if the frequencies are incommensurate, but I don't know if they are.
By the way, a less exotic way to combine many small contributions into a non-Gaussian result is simply not to add them, but to combine them in some non-linear manner, preferably one that can not be approximated well with a first-order Taylor series. For example, you get a log-normal distribution when you take the product of random variables. Not applicable to multitone tests, though.
Sound quality is mostly a subjective assessment so it has little to do with the thread title. A metric that would try to generalize subjective sound quality assessment is an oxymoron so better to stick with objective assessment. Subjective sound quality assessment should be left for the end user.
I would like to add some thoughts and experimental results on “capacitive loading” of the amplifier output. We have discussed a simple R//C loading and in case of a speaker cable we simplify its effect to a mere low-frequency capacitor. This is, however, incorrect and does not cover the reason why many amplifiers have failed without any reasonable explanation.
Cable reflections are usually not considered and cable HF properties are not considered important for audio amplifiers. There is an excellent application note AN-991 by Texas Instruments
https://www.ti.com/lit/an/snla043/snla043.pdf
that explains the cable reflections and shows many oscilloscope measurements of reflections due to load impedance mismatch. Yes audio frequencies cannot create such reflections in a speaker cable, but EMI induced high frequency signals or spikes due to SMPS or digital circuits action may initiate such reflections. Unfortunately, this phenomenon is generally not well understood.
Essentially, the cable driven from very low impedance (amp output) and having no termination (the speaker load would be inductive at frequencies >1MHz) is the worst case regarding reflections and oscillations. It is not the same case as to load the amplifier with a capacitor of the same capacitance value. Lumped or transmission line parameters start to be important.
Now, in case that the cable is terminated by a resistor with resistance near to cable characteristics impedance, the reflections and possible oscillations issue are highly suppressed. Another option is R-C series circuit to prevent LF loading.
To understand why a long cable may make an amplifier unstable, let's make the cable simulation.
First, we have a cable test circuit. The cable is driven from 0.001 ohm source and is terminated by 1Mohm resistor in parallel with 100pF capacitor.
10m coax cable impedance simulation
10m coax cable impedance measurement (open end)
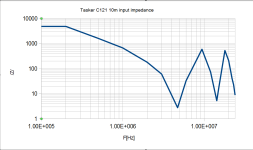
We can see 1st resonant peak at about 4.5MHz followed with decayed peaks, due to 1M//100pF termination. Please take into account that cable capacitance at impedance dips is in microfarads!
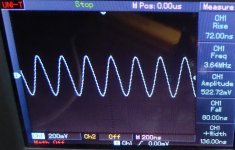
I have experience HF oscillations of the power amp under test when loaded with a long cable without load several times and the rise of amp case temperature was enormous. One example below.
Cable reflections are usually not considered and cable HF properties are not considered important for audio amplifiers. There is an excellent application note AN-991 by Texas Instruments
https://www.ti.com/lit/an/snla043/snla043.pdf
that explains the cable reflections and shows many oscilloscope measurements of reflections due to load impedance mismatch. Yes audio frequencies cannot create such reflections in a speaker cable, but EMI induced high frequency signals or spikes due to SMPS or digital circuits action may initiate such reflections. Unfortunately, this phenomenon is generally not well understood.
Essentially, the cable driven from very low impedance (amp output) and having no termination (the speaker load would be inductive at frequencies >1MHz) is the worst case regarding reflections and oscillations. It is not the same case as to load the amplifier with a capacitor of the same capacitance value. Lumped or transmission line parameters start to be important.
Now, in case that the cable is terminated by a resistor with resistance near to cable characteristics impedance, the reflections and possible oscillations issue are highly suppressed. Another option is R-C series circuit to prevent LF loading.
To understand why a long cable may make an amplifier unstable, let's make the cable simulation.
First, we have a cable test circuit. The cable is driven from 0.001 ohm source and is terminated by 1Mohm resistor in parallel with 100pF capacitor.
10m coax cable impedance simulation
10m coax cable impedance measurement (open end)
We can see 1st resonant peak at about 4.5MHz followed with decayed peaks, due to 1M//100pF termination. Please take into account that cable capacitance at impedance dips is in microfarads!
I have experience HF oscillations of the power amp under test when loaded with a long cable without load several times and the rise of amp case temperature was enormous. One example below.
Some time ago, there was a rather similar issue with a phono preamplifier. The turntable featured a switch that shorted the cartridge when the record stopped. As a result, the cable acted as a quarter-wave resonator, destabilizing the phono amplifier. Rectification effects then caused a huge bang when the record stopped.
A speaker cable will be less likely to cause oscillations because it has some internal loss. A capacitor at the output terminals is best because the phase margin will be lowest. But the inductance, you ask? Well you just use a lower value capacitor. The amp is unstable at set frequencies and it doesn't matter the ratio of capacitance to inductance as long as the loss is low enough. If you add inductance to the capacitor you will be improving phase margin due to the extra loss of the inductor.
The problem has shown even with "thick" cables, it is about cable distributed parameters only.
Your answer says you have not experienced this and you will not admit a strictly technical reason. It is fine, wait until you will once get the same issue. Amplifer output coil of course fixes the issue completely. I can see no more reason to share my experience, please stick with R, L, C simplest parameter explanations.
But even lumped cable model shows the issue with the specific amplifier.
Again, no need for me to debate or argue.
I meant to say a higher value capacitor. If you can get that amplifier to oscillate with a 10 meter cable then you can get it to oscillate with a capacitor, but the value of the capacitor must be larger without the added inductance of the cable. The amp doesn't care whether the impedance at it's terminals is due to reflections or bulk components.
I made a lot of errors. The amp can oscillate within a fixed range of frequencies. Your output cable hits within that range. Replace it with a capacitor large enough to oscillate at the same frequency. This is not hard to simulate.
At any single frequency, an RLC model is fully sufficient to show instability. If you need to model a range of frequencies you need a distributed model, but the amp only oscillates at one frequency. At the frequency of oscillation, there is only one phase and one magnitude. Nonlinear effects only occur after the oscillation has already begun.
Even when it oscillates at two frequencies simultaneously, the stability criteria for each individual frequency is fully satisfied by the phase and magnitude at that frequency.
Even when it oscillates at two frequencies simultaneously, the stability criteria for each individual frequency is fully satisfied by the phase and magnitude at that frequency.
Last edited: