Applicable article available at: https://www.researchgate.net/publication/236340550_Quantization_and_Dither_A_Theoretical_Survey
There is some hint on the web that the ESP8266 uses some hardware random number generator. I have to search about it. If not, a pseudo random number could be generated in software. Related discussion:
https://forum.arduino.cc/t/any-details-of-the-esp8266-hardware-random-number-generator/569602
https://forum.arduino.cc/t/any-details-of-the-esp8266-hardware-random-number-generator/569602
True random number generators tend to be too slow for direct use in computers. Instead, they seed a pseudo-random number generator.
Ed
Ed
STM32H7 true random number uses thermal noise and ADC. It works with up to 250MHz clock. Consecutive numbers take 40 clock cycles. Is that too slow?
It depends on what the random numbers are used for.
A web search says the STM32H7 true random numbers are 32-bit.
A software PRNG would take only a few clocks and can run on every CPU core.
Ed
A web search says the STM32H7 true random numbers are 32-bit.
A software PRNG would take only a few clocks and can run on every CPU core.
Ed
This discussion was about using RNG for dither. No doubt PRNG is faster but certified TRNG should be statistically uniform.
A PRNG seeded by a TRNG will produce numbers that are indistinguishable from true random numbers provided that the period is sufficiently long (easy to do).
Ed
Ed
There is some published research that tends to question how random audio dither needs to be for some audio applications. A short excerpt from an AES paper by Paul Findle (for example, item i):

Frindle goes on to explain that seeding of a random number generator wasn't enough for what he was doing. Each channel of a professional digital mixer had to have a completely separate random number generation algorithm or some mix engineers could learn to hear quantizing distortion through the dither. https://www.diyaudio.com/community/threads/paul-frindle-is-this-truth-or-myth.371790/
Frindle goes on to explain that seeding of a random number generator wasn't enough for what he was doing. Each channel of a professional digital mixer had to have a completely separate random number generation algorithm or some mix engineers could learn to hear quantizing distortion through the dither. https://www.diyaudio.com/community/threads/paul-frindle-is-this-truth-or-myth.371790/
Markw4 - That may have been due to self-correlation, which is something that a PRNG algorithm needs to avoid.
Ed
Ed
Back in 2015, when I designed the digital part of my valve DAC (implemented in an FPGA), I needed random or pseudorandom number generators for dithering. I didn't find any practical way to make a fast true random number generator, so I settled for pseudorandom with partly random seed.
A colleague had told me that maximum-length sequences from simple linear-feedback shift registers are often not very good and that there is a lot of literature about that, so I attempted to read up on that. I didn't understand much of the articles I read (they all appeared to be meant for pseudorandom number experts, which I am not), but I did learn something:
1. Maximum-length bit sequences can have bad subsequences with lots of autocorrelation.
2. There are many pseudorandom number generator algorithms, for example simple linear-feedback shift registers, linear congruential generators, Mersenne Twister, XORSHIFT variants such as XORSHIFT128+. The ones I just listed are all related to each other in some way or other.
3. There are test suites to check how randomly pseudorandom number generators behave, with peculiar names such as Diehard and Dieharder. Apparently there are experts attempting to find pseudorandom algorithms that pass these test suites and other experts trying to make the test suites harder to pass.
4. Apparently the very best PRNGs are called cryptographically secure, but almost none meet this criterion.
5. The so-called Hull-Dobell theorem tells you whether a linear congruential generator uses as much of its state space as possible, but when it does so in a regular manner, you still have a lousy pseudorandom number generator.
After that, I just picked a XORSHIFT128+ because it was easy to implement on an FPGA and it is apparently not bad.
A colleague had told me that maximum-length sequences from simple linear-feedback shift registers are often not very good and that there is a lot of literature about that, so I attempted to read up on that. I didn't understand much of the articles I read (they all appeared to be meant for pseudorandom number experts, which I am not), but I did learn something:
1. Maximum-length bit sequences can have bad subsequences with lots of autocorrelation.
2. There are many pseudorandom number generator algorithms, for example simple linear-feedback shift registers, linear congruential generators, Mersenne Twister, XORSHIFT variants such as XORSHIFT128+. The ones I just listed are all related to each other in some way or other.
3. There are test suites to check how randomly pseudorandom number generators behave, with peculiar names such as Diehard and Dieharder. Apparently there are experts attempting to find pseudorandom algorithms that pass these test suites and other experts trying to make the test suites harder to pass.
4. Apparently the very best PRNGs are called cryptographically secure, but almost none meet this criterion.
5. The so-called Hull-Dobell theorem tells you whether a linear congruential generator uses as much of its state space as possible, but when it does so in a regular manner, you still have a lousy pseudorandom number generator.
After that, I just picked a XORSHIFT128+ because it was easy to implement on an FPGA and it is apparently not bad.
MarcelvdG - That is a good summary. 128-bits is a good length LFSR for audio.
"Linear congruential" is the dinosaur-era-of-computing algorithm that I was referring to in post #62.
Mersenne Twister has been the state-of-the-art PRNG for over two decades. It is widely-used in software. A downside is that the state is so long that it is hard to seed.
"Cryptographically secure" requires that the internal state cannot be deduced from the sequence of pseudo-random numbers. This is accomplished by applying a "tempering" function to the output.
I took the middle ground and implemented a 782-bit maximal-length LFSR with a simple tempering function in one of my software libraries. It is overkill for audio, but I also use it to drive probabilistic simulators.
I wrote tests for randomness, wrote programs to display the output, and even listened to it. 🙂
I am not a PRNG expert. This is just a hobby.
Ed
"Linear congruential" is the dinosaur-era-of-computing algorithm that I was referring to in post #62.
Mersenne Twister has been the state-of-the-art PRNG for over two decades. It is widely-used in software. A downside is that the state is so long that it is hard to seed.
"Cryptographically secure" requires that the internal state cannot be deduced from the sequence of pseudo-random numbers. This is accomplished by applying a "tempering" function to the output.
I took the middle ground and implemented a 782-bit maximal-length LFSR with a simple tempering function in one of my software libraries. It is overkill for audio, but I also use it to drive probabilistic simulators.
I wrote tests for randomness, wrote programs to display the output, and even listened to it. 🙂
I am not a PRNG expert. This is just a hobby.
Ed
How do you get, say, a 32 bit uniformly distributed pseudorandom signal with negligible autocorrelation out of an LFSR? Clock it 32 times, or use some postprocessing? You can't just use 32 taps of the shift register or you get lots of autocorrelation.
Off topic: an interesting thing about linear congruential generators is that a digital first-order single-bit sigma-delta modulator is in fact a linear congruential generator. That means that the criteria of the Hull-Dobell theorem can help you to design digital sigma-delta modulators such that they use a large state space.
Off topic: an interesting thing about linear congruential generators is that a digital first-order single-bit sigma-delta modulator is in fact a linear congruential generator. That means that the criteria of the Hull-Dobell theorem can help you to design digital sigma-delta modulators such that they use a large state space.
Last edited:
The output of a maximal-length LFSR is almost perfectly uniformly-distributed: the LFSR produces exactly one more "1" than "0" over its entire period. Practical applications will never use the entire period.
The output function makes the internal state hard to guess. A non-linear function (AND/OR then XOR) makes the internal state impossible to guess. Be careful about uniformity. 🙂
Yes, simple self-correlation can be avoided by shifting 32 times to produce a 32-bit number, or 64 times to produce a 64-bit number. In software, all bits are computed in parallel. The tap and output bit indices must not overlap, which means that the shift register must have several times the width of the output. The shift register is "shifted" by incrementing pointers to a circular queue modulo the queue size.
I am not sure about more complicated forms of self-correlation, but I believe that placing the taps far apart is better.
Your statement about linear congruential being related to delta-sigma does not surprise me because linear congruential is based on arithmetic (multiplication and division). That is fine for shorter periods (<<64-bits), but for longer periods, shifting is easier than arithmetic. Not having to move data makes the circular queue even easier.
Ed
The output function makes the internal state hard to guess. A non-linear function (AND/OR then XOR) makes the internal state impossible to guess. Be careful about uniformity. 🙂
Yes, simple self-correlation can be avoided by shifting 32 times to produce a 32-bit number, or 64 times to produce a 64-bit number. In software, all bits are computed in parallel. The tap and output bit indices must not overlap, which means that the shift register must have several times the width of the output. The shift register is "shifted" by incrementing pointers to a circular queue modulo the queue size.
I am not sure about more complicated forms of self-correlation, but I believe that placing the taps far apart is better.
Your statement about linear congruential being related to delta-sigma does not surprise me because linear congruential is based on arithmetic (multiplication and division). That is fine for shorter periods (<<64-bits), but for longer periods, shifting is easier than arithmetic. Not having to move data makes the circular queue even easier.
Ed
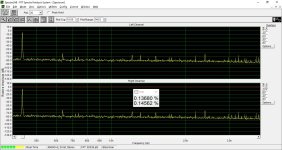
I want to know, what is the minimum possible THD at -60db level for 16 bit DAC?
Here is an measurement made of an TDA1541A non oversampling full passive , without any kinda filtering :
dont know if it's the minimum possible for an 16 bit DAC , but it doesn't seam's that far 🙂
.
Last edited:
- Home
- Source & Line
- Digital Line Level
- 16 bit DAC AT-60DB