I'm starting this thread to talk about an interesting and new method for "removing" group delay from a continuous audio signal using reverse-IIR filtering.
Background: When you perform "analog style" filtering on a signal, that filter does not output all frequencies at the same time. Instead, frequencies emerge from the filter at different times. This is a consequence of what the filter is doing in the frequency domain (e.g. to the frequency response) - the filter automatically produces non-linear phase changes to the output signal. The result is a distortion of the time-domain waveform, because the appearance in time of various passed frequency components has been altered compared to the input. This sort of phase-domain distortion does not in any way change the magnitude of the frequency component (the frequency response) but the signal in the time domain may look badly distorted. This effect is called by different names, including phase distortion and group delay distortion. When the distortion grows large enough, it is possible to perceive a change to the "tone" of the signal. At lower levels it becomes imperceptable/inaudible. in general, the steeper the filter the worse the group delay distortion and this puts some limits on how steep of a filter we can use for a loudspeaker crossover. With FIR filtering, the situation is different. Phase and amplitude of the filter are independent of each other and this means it is possible to choose the phase to be linear (meaning the group delay is flat). Until now, FIR processing was essentially (to the best of my knowledge) the only practical way to implement a filter with a linear phase response.
More Background: Forward-Backward IIR processing. Someone realized that if you had some finite quantity of sampled audio you could process it first in the normal "forward" direction, and then also in the "backwards" direction. The filter's magnitude changes are applied twice. But the changes in the phase of the signal are exactly reversed, undone, and set back to zero in the "reverse" pass of the filter. What is happening is that the time shift of a given frequency that occurs in the forward direction is exactly equal to the time shft from the reverse pass, but these are opposite in their time "direction" and so they cancel. The result is zero phase distortion, zilch, nada! Let's do it says the crowd. Ah, but implementing this is not so simple. In the forward pass the ringing tail of the signal requires some time to "die down" This extends the duration of the original signal by the length of the tail. This tail must also be processed in the reverse pass in order for it to be brought back in time to its original "place". But if you have a continuous signal, things get tricky. There have been attempts at overlap-and-add methods to process chunks of a continuous signal and then sort of stitch them together but this typically leads to end effects and other problems, and the algorithm is a bit messy.
To the rescue and something that I belive is completely novel is the work by Martin Vicanek that is described in his whitepaper "A New Reverse IIR Filtering Algorithm":
https://www.vicanek.de/articles/ReverseIIR.pdf
I will not get into the gory details of the algorithm too much here. However, in the whitepaper Martin describes a way to take the "Infinite Impulse Response" of the IIR filter, truncate it to make it an FIR response, and then reverse the FIR as blocks in order to reverse the poles of the filter. It's frankly some brilliant work that completely eliminates the need for block processing. The only inputs to the algorithm are previous INPUT samples. There is no longer the feedback from output samples because of the re-formulation of the IIR as an FIR (which is then reversed). This allows for continuous "forward only" processing of the audio signal, and this can go on indefinitely. Best of all, the number of operations required for the processing is much less than the equivalent FIR and latency is much less than reverse-IIR block processing methods.
So, how does this help with loudspeaker group delay? While reading Martin's whitepaper I recalled that the group delay from the summed outputs of an Nth order crossover (the sum of the lowpass and highpass filters that make up the crossover) is the same as the group delay from an all-pass filter of order N/2. An example of this is a 4th order Linkwitz-Riley crossover, which is constructed from two second order Butterworth filter (each having the same pole frequency and Q=0.707) run in series. The LR4 has the EXACT same group delay as a second order allpass filter with the same Fc and Q. So, to make a linear phase LR4 crossover we can implement the allpass response, "in reverse" via the RIIR filter, upstream of the crossover to "pre-distort" the phase of the signal so that after it passes through the LR4 and undergoes an "in air" summation the phase remains unchanged.
The applicability of this technique is very broad. This is because we only need to find the group delay response of the loudspeaker that results from the crossover filters and other sources of delay, construct approximately the same group delay response using only all-pass filters, and then apply those all-pass filters in reverse using the RIIR filter. It doesn't matter what order the crossover may be or what the source of the group delay, as long as you can model or measure it you can cancel most or all of it depending on how close a match you can get via allpass filters. My recent effort to do some group delaey audibility testing, as well as what has been repoted in the literature about group delay, indicates that group delay does not need to be zero but only below some threshold to remain inaudible because human hearing is just not all that sensitive to it. But what (to me) is interesting as someone interested in new frontiers in crossover design, is that filters that previous had too high of a group delay response because they were "very steep" can now be corrected to have as low of a group delay as you wish. This starts to blur the lines between IIR and FIR processing and what each type can accompllish, and I find that pretty interesting stuff.
So, are there any downsides? Well, not really but there is a consequence to the RIIR algorithm: latency. When I described how the algorithm works, above, I mentioned that the IIR impulse response is truncated to become an FIR filter. This truncation introduces error because you are at some point setting the remaining part of the impulse "tail" to zero. This is a source of error or noise in the output signal. The more of the tail you retain, the lower is the added "noise" signal. Luckily Martin provides a way to determine how much of the tail needs to be retained when given some signal to noise ratio that is desired. Also, because the tails from poles located at lower frequencies last longer than for higher frequencies, RIIR filtering for filters with lower pole frequencies requires increasing latency. But luckily the tail decays exponentially, and so the latency is not too severe. In a test trial I ran a 1kHz 2nd order allpass as an RIIR filter. This required 128 samples of latency at 96kHz, which is a latency of 1.33 milliseconds. It's a small price to pay indeed.
I have created LADSPA plugins that implement the RIIR algorithm for first and second order allpass filters. These can be used for phase and group delay equalization and linearization. As of 27SEPT2024 these are available for download at my LADSPA page:
http://audio.claub.net/LADSPA-plugins.html
I will post some follow up information including some more specific examples soon. For now I thought I would put this out there to start a discussion and raise awareness of this processing algorithm.
Background: When you perform "analog style" filtering on a signal, that filter does not output all frequencies at the same time. Instead, frequencies emerge from the filter at different times. This is a consequence of what the filter is doing in the frequency domain (e.g. to the frequency response) - the filter automatically produces non-linear phase changes to the output signal. The result is a distortion of the time-domain waveform, because the appearance in time of various passed frequency components has been altered compared to the input. This sort of phase-domain distortion does not in any way change the magnitude of the frequency component (the frequency response) but the signal in the time domain may look badly distorted. This effect is called by different names, including phase distortion and group delay distortion. When the distortion grows large enough, it is possible to perceive a change to the "tone" of the signal. At lower levels it becomes imperceptable/inaudible. in general, the steeper the filter the worse the group delay distortion and this puts some limits on how steep of a filter we can use for a loudspeaker crossover. With FIR filtering, the situation is different. Phase and amplitude of the filter are independent of each other and this means it is possible to choose the phase to be linear (meaning the group delay is flat). Until now, FIR processing was essentially (to the best of my knowledge) the only practical way to implement a filter with a linear phase response.
More Background: Forward-Backward IIR processing. Someone realized that if you had some finite quantity of sampled audio you could process it first in the normal "forward" direction, and then also in the "backwards" direction. The filter's magnitude changes are applied twice. But the changes in the phase of the signal are exactly reversed, undone, and set back to zero in the "reverse" pass of the filter. What is happening is that the time shift of a given frequency that occurs in the forward direction is exactly equal to the time shft from the reverse pass, but these are opposite in their time "direction" and so they cancel. The result is zero phase distortion, zilch, nada! Let's do it says the crowd. Ah, but implementing this is not so simple. In the forward pass the ringing tail of the signal requires some time to "die down" This extends the duration of the original signal by the length of the tail. This tail must also be processed in the reverse pass in order for it to be brought back in time to its original "place". But if you have a continuous signal, things get tricky. There have been attempts at overlap-and-add methods to process chunks of a continuous signal and then sort of stitch them together but this typically leads to end effects and other problems, and the algorithm is a bit messy.
To the rescue and something that I belive is completely novel is the work by Martin Vicanek that is described in his whitepaper "A New Reverse IIR Filtering Algorithm":
https://www.vicanek.de/articles/ReverseIIR.pdf
I will not get into the gory details of the algorithm too much here. However, in the whitepaper Martin describes a way to take the "Infinite Impulse Response" of the IIR filter, truncate it to make it an FIR response, and then reverse the FIR as blocks in order to reverse the poles of the filter. It's frankly some brilliant work that completely eliminates the need for block processing. The only inputs to the algorithm are previous INPUT samples. There is no longer the feedback from output samples because of the re-formulation of the IIR as an FIR (which is then reversed). This allows for continuous "forward only" processing of the audio signal, and this can go on indefinitely. Best of all, the number of operations required for the processing is much less than the equivalent FIR and latency is much less than reverse-IIR block processing methods.
So, how does this help with loudspeaker group delay? While reading Martin's whitepaper I recalled that the group delay from the summed outputs of an Nth order crossover (the sum of the lowpass and highpass filters that make up the crossover) is the same as the group delay from an all-pass filter of order N/2. An example of this is a 4th order Linkwitz-Riley crossover, which is constructed from two second order Butterworth filter (each having the same pole frequency and Q=0.707) run in series. The LR4 has the EXACT same group delay as a second order allpass filter with the same Fc and Q. So, to make a linear phase LR4 crossover we can implement the allpass response, "in reverse" via the RIIR filter, upstream of the crossover to "pre-distort" the phase of the signal so that after it passes through the LR4 and undergoes an "in air" summation the phase remains unchanged.
The applicability of this technique is very broad. This is because we only need to find the group delay response of the loudspeaker that results from the crossover filters and other sources of delay, construct approximately the same group delay response using only all-pass filters, and then apply those all-pass filters in reverse using the RIIR filter. It doesn't matter what order the crossover may be or what the source of the group delay, as long as you can model or measure it you can cancel most or all of it depending on how close a match you can get via allpass filters. My recent effort to do some group delaey audibility testing, as well as what has been repoted in the literature about group delay, indicates that group delay does not need to be zero but only below some threshold to remain inaudible because human hearing is just not all that sensitive to it. But what (to me) is interesting as someone interested in new frontiers in crossover design, is that filters that previous had too high of a group delay response because they were "very steep" can now be corrected to have as low of a group delay as you wish. This starts to blur the lines between IIR and FIR processing and what each type can accompllish, and I find that pretty interesting stuff.
So, are there any downsides? Well, not really but there is a consequence to the RIIR algorithm: latency. When I described how the algorithm works, above, I mentioned that the IIR impulse response is truncated to become an FIR filter. This truncation introduces error because you are at some point setting the remaining part of the impulse "tail" to zero. This is a source of error or noise in the output signal. The more of the tail you retain, the lower is the added "noise" signal. Luckily Martin provides a way to determine how much of the tail needs to be retained when given some signal to noise ratio that is desired. Also, because the tails from poles located at lower frequencies last longer than for higher frequencies, RIIR filtering for filters with lower pole frequencies requires increasing latency. But luckily the tail decays exponentially, and so the latency is not too severe. In a test trial I ran a 1kHz 2nd order allpass as an RIIR filter. This required 128 samples of latency at 96kHz, which is a latency of 1.33 milliseconds. It's a small price to pay indeed.
I have created LADSPA plugins that implement the RIIR algorithm for first and second order allpass filters. These can be used for phase and group delay equalization and linearization. As of 27SEPT2024 these are available for download at my LADSPA page:
http://audio.claub.net/LADSPA-plugins.html
I will post some follow up information including some more specific examples soon. For now I thought I would put this out there to start a discussion and raise awareness of this processing algorithm.
Last edited:
I forgot to mention that this can also be applied to a loudspeaker with a passive crossover. The RIIR filters are inserted into the playback chain before the amplifier. So you could correct the phase or group delay of any loudspeaker with this method.
This would make for a great A/B/X listening test on the audibility of group delay! Let's see if all of those "linear phase" proponents can actually tell the difference in a blind test...
This would make for a great A/B/X listening test on the audibility of group delay! Let's see if all of those "linear phase" proponents can actually tell the difference in a blind test...
Charlie, Great to see you continuing to explore this topic.
I don't have near the depth with filter theory, particularly IIR, that you do, but I've tried or at least studied many different techniques for achieving linear-phase xovers, with the minimum amount of fixed delay (latency).
(I don't really care anymore about achieving computational efficiency...seems to become ever more moot as Moore's law marches on.)
Anyway, I've come to a few conclusions (that I'll be happy to discard when shown they are in err.)
One big conclusion, is that it takes time to correct time.
Which means to me, all time correcting/phase flattening techniques, be they FIR, a boat load of IIR all-pass filters,
or the reverse-IIR presented in the paper.....will end up having the same latency, to do the same task.
And of course, the lower the frequency, the longer the wavelengths and their response tails, the more the latency for any/all of them.
I've found xovers themselves are a pretty easy task for linearizing-phase, even higher order, because they have rather smooth and continuous curves.
Combine that with a moderately high 1 kHz xover point, and it takes very little latency to make a linear-phase crossover there using FIR..
For instance, the 1 kHz LR24 used in the RIIR example, can be performed equally well with a regular linear phase FIR xover using the same 128 samples at 96kHz, with the same 1.33ms latency.
No free lunch...sigh. Back to it takes time to correct time, I think.
I don't have near the depth with filter theory, particularly IIR, that you do, but I've tried or at least studied many different techniques for achieving linear-phase xovers, with the minimum amount of fixed delay (latency).
(I don't really care anymore about achieving computational efficiency...seems to become ever more moot as Moore's law marches on.)
Anyway, I've come to a few conclusions (that I'll be happy to discard when shown they are in err.)
One big conclusion, is that it takes time to correct time.
Which means to me, all time correcting/phase flattening techniques, be they FIR, a boat load of IIR all-pass filters,
or the reverse-IIR presented in the paper.....will end up having the same latency, to do the same task.
And of course, the lower the frequency, the longer the wavelengths and their response tails, the more the latency for any/all of them.
I've found xovers themselves are a pretty easy task for linearizing-phase, even higher order, because they have rather smooth and continuous curves.
Combine that with a moderately high 1 kHz xover point, and it takes very little latency to make a linear-phase crossover there using FIR..
For instance, the 1 kHz LR24 used in the RIIR example, can be performed equally well with a regular linear phase FIR xover using the same 128 samples at 96kHz, with the same 1.33ms latency.
No free lunch...sigh. Back to it takes time to correct time, I think.
Hmm, didn't check the paper or other stuff yet, but as I understood FIR filter has symmetric impulse which means pre-echo, but which cancels out with output from the other device if it's a crossover. On a point source system pre-echo is thus not an issue, but on a stacked multiway the pre-echo would show up vertical off-axis. How about with the RIIR, does it have the pre-echo and trade-off in this sense?
All of the concerns like this that apply to FIR filtering also apply to the reverse-IIR filtering. That is because this approach is basically some FIR filtering combined with regular IIR filtering. I suppose it it even like using a rectangular window on an FIR impulse response.
Regarding the computational effort, supposedly this requires several times fewer operations than the equivalent FIR filter. The whitepaper ends with :
Regarding the computational effort, supposedly this requires several times fewer operations than the equivalent FIR filter. The whitepaper ends with :
I am only repeating what the author has claimed. I did not verify this myself, but I can say from the code I wrote that it's very simple, computationally speaking.
This is not a delay plug in!
The RIIR adds "negative frequency dependent delay" and I am describing an application of that to counteract the group delay that the crossover filters create.
FWIW, playing with RePhase I find that to get an almost perfect phase-unwrapper for a 1kHz LR4 @ 96kHz you need a bit more than 128 samples, like 192 samples. Which means 96 samples (1ms) of intrinsic delay. The additional block processing delay of a standard convolver can be reduced by overlap-and-add method which of course comes with a penalty, more computations.
@CharlieLaub , I think the main benefit of RIIR, the reduced computational effort, will be at lower frequencies, like a correction for a LR4 @ 80Hz subwoofer-to-main XO, where the phase unwrapping is so much more important than at 1kHz and above.
Last edited:
Yep, I also think more than 128 samples would be needed with standard FIR widowing.
I saw it takes rectangular windowing with 128 samples, to more fully eliminate slippage error. Don't think I'd want to do that though...
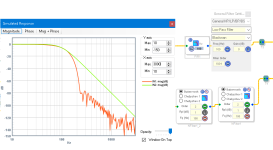
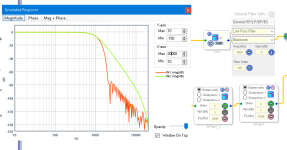
I think you will all be surprised what this can do... I can only tell you that I ran my plugin on an LR4 with Fc=1kHz @ 96kHz and with the SNR set to a min of 60dB (see whitepaper link in first post) the remaining phase distortion on a 20Hz square wave signal is practically zero. This required latency of 128 samples. I am attaching the output as a mono WAV file. I am also attaching a picture of the original WAV, after processing through the LR4 (sum of LP and HP outputs), and then after using the RIIR to remove the phase distortion. Looks like this:
And if the cutoff frequency is 100 Hz, you will also need 128 samples to compensate for phase distortion?
I think the number of taps will need to be increased....
I am very weak in the mathematics of digital signal processing. More precisely, I have zero knowledge in this area, so I understand the results of experiments better.
I would like to see the waveform after LP and separately after HP before summing them.
I think you meant to say xover frequency, right?
Charlie, could you run 128 samples for a 100 Hz crossover?
Um, no. Sorry I thought that was kind of obvious! OK, but why not 128 samples at 100Hz? It is because the tail of a low frequency pole is much longer than for a high frequency pole. I assume the length of the tail is proportional to frequency, so 10 times longer at 100Hz than for 1k Hz. Assuming that is true, the latency incurred is a power of 2 samples because of how the algorithm operates, so either 1024 or 2048 samples. This is actually a user-adjustable parameter (see paper, SNR, equation 2) so it could be less than this.
The processing is very different from FIR/DFT. There are N stages, each with a delay of 2^N samples. It is only the LAST sample in the delay pipe that is used in the actual calculation. The other 2^N-1 samples are just moving along until they in turn reach the end of the ring buffer and are used. In each stage the calculation has the form a*x + b*y + c, so the calculation is actually extremely lightweight! Nevertheless, you have to wait for the sample to reach the end of the longest delay pipe to have 100% correct output. Still, even 2048 samples at 96kHz is only 21 milliseconds of latency.
The processing is very different from FIR/DFT. There are N stages, each with a delay of 2^N samples. It is only the LAST sample in the delay pipe that is used in the actual calculation. The other 2^N-1 samples are just moving along until they in turn reach the end of the ring buffer and are used. In each stage the calculation has the form a*x + b*y + c, so the calculation is actually extremely lightweight! Nevertheless, you have to wait for the sample to reach the end of the longest delay pipe to have 100% correct output. Still, even 2048 samples at 96kHz is only 21 milliseconds of latency.
Last edited:
Well, with such arithmetic, I don't see much sense in such an approach. Using the classic FIR at 1024 taps, we can get a filter cutoff steepness 100 Hz higher than that of LR4, while we are guaranteed to have a flat phase at the cutoff frequency.
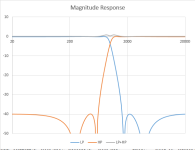
Below on the frequency response, in red is FIR 1024 and in green is LR4.
Well, for clarity, FIR 128 taps per 1 kHz.
Last edited:
Here is another example. After I talked to the whitepaper author (Martin Vicanek) about my idea to use an allpass in the reverse-IIR filter to do group delay EQ he did a little trial. He created a 4th order elliptical filter LP, HP pair having fc=1kHz and summed them. Next he calculated the group delay of the sum and did a rough approximation with a 2nd order allpass filter by comparing their impulse responses (see pic). It's not exact but pretty close - the elliptical filter has a double peak in the GD. Then he applied the RIIR filter upstream of the elliptical crossover and computed the new impulse response, and it was extremely clean, but delayed due to the latency of the RIIR filter. He reported that to me as 64 samples at 44.1kHz. If you are used to looking at the impulse response produced by crossover filters, this should be impressive.
Pics attached. I will try to think up some other examples to show, perhaps one with Fc=100Hz?
I'm off to bed here.
Pics attached. I will try to think up some other examples to show, perhaps one with Fc=100Hz?
I'm off to bed here.
Attachments
Well for one, you don't need to use FIR at all. That's a plus in my book!