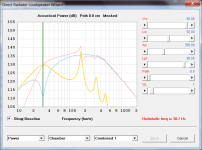
Now it seems it doesn't solve much of a problem at all really. In my design, the 40Hz port tuned one, at 40Hz the cone radiator is -17dB to the port. So even with the cone being out of phase to the port, the port produces very major part of the output, to a point of cone being insignificant enough to ignore for the problem at hand.
Therefore, we are talking about a port, producing nearly 60 Watts of acoustical power to create 132.6dB, while the design producing half the acoustical power can do the same SPL. Is it all hidden in the radiation area and directivity, or are we leaving something out?
Still wonder about the port being out of phase. Seems to be contradictory at firts glance, but uneducated look at the plot shows 90 degrees shift indeed.
Your port will basically be out of phase. This is a safe assumption. But, there is group delay in the real world that will make this not 100% accurate. Length of port, size of enclosure. Diameter of port, shape of port. Al these things will effect the group delay. Phase is the signal in comparison with time. And there is also a space vector involved. As we are looking at a phase graph we are basically looking at a messy helical pattern drill bit on it's side. a 2 Dimensional representation of a 3 Dimensional measurement. If you look at a drill bit on it's sharp end you see little of what else is behind it. When you look along it's edge, you have something of the design of the drill bit, but not all of it. Same for phase. It is always a little more complicated.
I see, and I am slowly calming down, being less jumpy, taking in the new reality. Now I wonder if it is the right thinking, if given the output of the cone of the "tuned-in" system can be basically ignored, it is right thinking that the difference boils down to the radiation area.
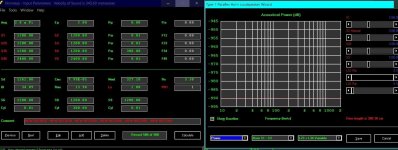
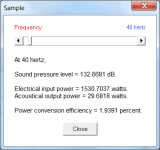
At 40 Hz the acoustical output power radiating from the port in the 40 Hz system is 58.6315 watts, as shown in the screenprint below.
The resulting SPL is calculated as follows:
The port is assumed to be a point source at the centre of a sphere with a radius of 1 metre.
The surface area of the sphere = 4 * Pi * Radius ^ 2 = 4 * Pi * 1 ^ 2 = 4 * Pi square metres.
The 40 Hz design specifies Ang = 1.0 x Pi or quarter space so that the point source radiates into a quarter of a sphere with a surface area of (4 * Pi) / 4 = 1 * Pi square metres (the same numerical value as Ang).
The pressure at the surface of the quarter sphere is given by:
Pressure = (Power * c * rho / Area) ^ 0.5
Where:
c = velocity of sound in air (344 metres per second)
rho = density of air (1.205 kilograms per cubic metre)
Area = quarter sphere surface area (1 * Pi square metres)
Therefore:
Pressure = (58.6315 * 344 * 1.205 / Pi) ^ 0.5 = 87.9556 pascals
SPL = 20 * Log10( Pressure / Reference_Pressure)
Where:
Reference_Pressure = 20 micropascals = 20 * 10 ^ -6 pascals
Therefore:
SPL = 20 * Log10(87.9556 / (20 * 10 ^-6)) = 132.8647 dB
Exactly as shown below.
Hornresp Update 5630-240823
Hi Everyone,
CHANGE
The main headings in the Contents section of the Help file now have either an up or a down symbol, rather than just a down symbol.
Previously an uppercase "V" was included at the beginning of the main headings whether or not their related sub-headings were visible, as shown in Attachment 1.
Now a lowercase "v" is included at the beginning of main headings that do not have their related sub-headings visible, and a "^" symbol is included at the beginning of main headings that do have their related sub-headings visible, as shown in Attachment 2.
Kind regards,
David
Hi Everyone,
CHANGE
The main headings in the Contents section of the Help file now have either an up or a down symbol, rather than just a down symbol.
Previously an uppercase "V" was included at the beginning of the main headings whether or not their related sub-headings were visible, as shown in Attachment 1.
Now a lowercase "v" is included at the beginning of main headings that do not have their related sub-headings visible, and a "^" symbol is included at the beginning of main headings that do have their related sub-headings visible, as shown in Attachment 2.
Kind regards,
David
Attachments
@David McBean
This is it. I figured that the port in this design indeed is the major radiator.
The math you wrote is clear (Although I need to dust off my logarithms).
Now what is the difference between the 30Hz design with both port and cone working together? It is not assumed to be a point source? I admit, this is where I fail. Because if the port has not an enemy eating up on the efficiency and SPL, then I am lost where the dual source of cone and port gains on it with half the output power. I would firstly assume that the 40Hz design gets its pressure lost by phase issues. Without it, I'm lost. Many thanks for patience.
This is it. I figured that the port in this design indeed is the major radiator.
The math you wrote is clear (Although I need to dust off my logarithms).
Now what is the difference between the 30Hz design with both port and cone working together? It is not assumed to be a point source? I admit, this is where I fail. Because if the port has not an enemy eating up on the efficiency and SPL, then I am lost where the dual source of cone and port gains on it with half the output power. I would firstly assume that the 40Hz design gets its pressure lost by phase issues. Without it, I'm lost. Many thanks for patience.
990dB SPL ?
well now you can annoy our neighbors in MARS 🤣
well now you can annoy our neighbors in MARS 🤣
The locations of ‘perfect’ cancelation in qw pipes (TH or PH or CH modes) sum ‘perfectly’ out of phase at wavelengths 4, 8,12,16.. x the 1/4 wavelegth in the response. also, if you add a resonator in series or parallel that’s at a harmonic length/relationship.
Or the entire thing if you use To identical pipes connected together in TH, PH or CH (with no ‘path’).
I found it intersting and helpful to create things that ‘lined up’ at those 1/4 wave intervals
Or the entire thing if you use To identical pipes connected together in TH, PH or CH (with no ‘path’).
I found it intersting and helpful to create things that ‘lined up’ at those 1/4 wave intervals
That indeed would make a tear even in quantum physics. It is an underbelt punch to test if the hornresp can be eFFed up/with to a point of failure, but oh well, I am guilty of that idea, someone saw it and realized it. As always. 😂 For that I applogize.
I am still stuck on that 30=60 though. No explanation on mind, the radiation area jab was just to push knowledgeale people to respond, but I don't believe even that.
If the hornresp did not do what I want, it would be fine as always. But now for me it looks like it does what it shouldn't. Not to attack it, asking for help. The monkey always assumes the fault is on the other side. Can handle being ridiculed when truth comes out.
I am still stuck on that 30=60 though. No explanation on mind, the radiation area jab was just to push knowledgeale people to respond, but I don't believe even that.
If the hornresp did not do what I want, it would be fine as always. But now for me it looks like it does what it shouldn't. Not to attack it, asking for help. The monkey always assumes the fault is on the other side. Can handle being ridiculed when truth comes out.
The 30 Hz design with both port and cone working together is modelled as two point sources having different output sound levels and phases. Because a zero path length has been specified there is no distance separating the two sources (they are co-located).
For the 30 Hz design:
Ang = 1.0 x Pi
Path = 0.0 cm
At 40 Hz:
PD = direct radiator sound pressure at 1 metre = 34.2017 pascals
PP = port sound pressure at 1 metre = 52.4084 pascals
Theta = phase difference = -0.2455 radians
Resultant sum of the two pressure vectors:
Pressure = (PD ^ 2 + PP ^ 2 + 2 * PD * PP * Cos(Theta)) ^ 0.5
Pressure = (34.2017 ^ 2 + 52.4084 ^ 2 + 2 * 34.2017 * 52.4084 * Cos(-0.2455)) ^ 0.5
Pressure = 85.9873 pascals
Resultant sound pressure level:
SPL = 20 * Log10(Pressure / Reference_Pressure)
SPL = 20 * Log10(85.9873 / (20 * 10 ^ -6))
SPL = 132.6681 decibels
Exactly the same as shown in Attachment 2.
There is probably little to be gained by taking this particular discussion any further. As I said before, I am confident that the Hornresp calculations are correct. I think you will find that the results are similar to those obtained using other reliable bass-reflex loudspeaker simulation programs.
Attachments
Last edited:
Mathematically the lowest theoretical SPL is actually minus infinity dB. Hornresp limits the value to -990 dB if no signal is present.
The lower threshold of human hearing is normally taken to be a pressure of 20 micropascals, equivalent to an SPL of 0 dB.
Last edited:
@David McBean
Thank you very much for explaining this.
It might be an offtopic now, just lack of knowledge (of physics). I am just seeking understanding and where the possible assumed discrepancy comes from. It narrows down to only possible answer to the problem. That I'm a dumbas, not knowing the trivial caveat. Actually knowing maybe, but not applying or considering it.
Given the presented data, you explained how these designs produce same pressure. Now I am stuck at how these are able to do that with different kind of acoustical power output. Lacking the knowledge.
Thank you very much for explaining this.
It might be an offtopic now, just lack of knowledge (of physics). I am just seeking understanding and where the possible assumed discrepancy comes from. It narrows down to only possible answer to the problem. That I'm a dumbas, not knowing the trivial caveat. Actually knowing maybe, but not applying or considering it.
Given the presented data, you explained how these designs produce same pressure. Now I am stuck at how these are able to do that with different kind of acoustical power output. Lacking the knowledge.
Last edited:
Okay, did the math, and it boils down somewhat to the radiation area or impedance. The single source does 58Watt at 87Pa, the dual source does 8.7+20.5W roughly, 34+52Pa. So the acoustical power still does not transfer to pressure or the SPL. Which is mindboggling. One would assume we are at the very end of the acoustical equation, yet it somehow isn't.
Because it's not perfectly in phase - if you did not consider that.
I did a measurement and showed the effect graphically:
https://www.diyaudio.com/community/...ox-woofers-out-of-fashion.412687/post-7684005
I will read on that, but this is not an argument here. Because we are not missing something on the two source case (SPL) that might not sum well. We have additional SPL on hand with half power. So arguably, even with out of phase sources, we have "too much" SPL. Given the mr. McBean's math, we see the phase issue is borderline negligible. The radiation of the two sources adds up almost perfectly. It is that with just 30Watts of radiation we get 132dB, which we get from single source also, but radiating 60Watts of acoustical power. With ChatGPT I am getting to the revelation that indeed, acoustical power does not transfer into SPL. Possibly due to the acoustical impedance matching. In the end, it looks like it is boiling down to the radiation area.
The issue here is in the word efficiency. If we take it bluntly, it is power in, versus power out, full stop, no adfitional words, expressed in %. The issue is, that this efficiency is now taken (more or less)arbitrarily like acoustical power, which appears to be a parameter which is borderline unconsequential to the use of speakers, because it does not transfer to sound pressure/level. As mentioned before, you can have two sources in opposition to each other, have mathematically 100% efficiency but zero dB. At that point such efficiency has no meaning for intended use. I would argue we need at least get the SPL output efficiency on top of that, to reap and read usable info on the design. One would thought that under word efficiency, the most important would be the meaning of input watts versus output decibels.
The issue here is in the word efficiency. If we take it bluntly, it is power in, versus power out, full stop, no adfitional words, expressed in %. The issue is, that this efficiency is now taken (more or less)arbitrarily like acoustical power, which appears to be a parameter which is borderline unconsequential to the use of speakers, because it does not transfer to sound pressure/level. As mentioned before, you can have two sources in opposition to each other, have mathematically 100% efficiency but zero dB. At that point such efficiency has no meaning for intended use. I would argue we need at least get the SPL output efficiency on top of that, to reap and read usable info on the design. One would thought that under word efficiency, the most important would be the meaning of input watts versus output decibels.