Hello Burnt,
No problem to add later this kind of test in my do (wish?) list if we think it is useful.
I have read this paper too... several times. Thanks to our exchange I come to a new understanding. Up to now, I was not able to match the proposed model of a randomly vibrating diaphragm with the modes of the plates which are clearly localized, very geometric. In fact I haven't read probably carefully enough another element which if the far field... The panel has a fixed position in the room, the listener too but the sources spot at different location on the membrane with the frequancy, which is quite large, creating at distance a pseudo random phase due to the pseudo random distances. This is (or might be) also true for the boundary reflections creating a much more complex combination situation of the front wave and the out of phase rear wave than with a single pistonic loudspeaker.
May I say now that I understand the title "When a Little Chaos is Good For You"?
Christian
I agree. One possibility is to push more the simulation up to the far field SPL. Need more knowledge in the simulation tools.
Sometime ago, I made a test of XPS 9mm in oval shape. It was probably one of the less even (smooth?) FR I get among my different tests, showing an important peak at some hundreds hertz. This is probably what you show here Eric.
Yes indeed that looks like a typical case. Degeneracy arises in situations of high symmetry where multiple mode shapes (or wave functions of quantum mechanics) can have the same energy, Introducing asymmetry removes the degeneracy. This is why you would never use a circle or square as a panel - the symmetry leads to very strong resonances at a few frequencies with big dips between. I wonder if there are degenerate modes arising from rectangular plates with integer multiple side lengths - that's the sort of thing we could test with fem.
My general philosophy for panel design is to eliminate symmetry wherever possible. If you must have 90 degree angles, or equal side lengths, then have intermittent damping or support etc.
In one sense, those two unique mode shapes are an artifact of the fem I think. In real systems, the two degenerate modes can mix in any proportion, so in practice eg a Chladni plate you would not see either mode by itself.
I understand why it might seem like integer multiple side lengths could be bad, but I have not seen evidence of that. At least not with simply supported plates. I just fiddled around with a 4:1 design with LISA, just to be sure I hadn't missed something previously. No really close modes. Certainly nothing like the multiple modes at the same frequency that I get with square plates or that ellipse that I shared.
I've played around with asymmetrical supports a little bit, in both modelling and building. So far I didn't find any benefit that was obvious. But I wouldn't be surprised if there are indeed benefits that I've missed.
I agree about the square or circle for sure.
Eric
What do you hear from your own ears in these experiments other than the microphone hearing (testing)? Which one, shape, size, material is better?
Hello Chdsl,
It was only testing to try to find an orientation and select some way.
+ @pway
Hello Eric, hello Paul
What I see from tests (FR at 1m) of different shapes or boundary conditions is that some "peaks" occur in the FR like if locally the density of modes was more important (this is an interpretation, the fact is there are peaks). Have you already think how to get some indication of that from the FEM simulations? Getting the SPL in far field might be a too big steps. Do we have intermediate possibility thanks too the options of FEM tools like getting some information of speed of the panel? Or in other words, what about the amplitude or speed aspect of the modes? The mode density is also possible candidate but i don't see for now the relation.
Christian
No, no conclusion. You can see the exchanges in parallel with the FEM approach. There are many parameters : the shape, the boundary conditions, the suspension material, the edge shape... any idea to separate that in "more simple" problems is welcome.
Have you looked at the Japanese guy's web site. Here's the link again. He has interesting idea about the point transfer of the sound to a flat surface fixed at all sides. There's about six long pages to read. By the way, he was selling his speakers $2600/pair. He calls it Jazzman as he loves Jazz, but it is a DML, one way or another. Have a read, the link translates to English automatically. I couldn't get a suitable spike to fix to transducer to test his theories yet, but his idea is interesting.
@pway
Paul,
In the Elmer documentation, I found this description of the boundary conditions available. Do you know the physical meaning of the highlighted parameters? Do you know what the vectors n and t are referring to? I'm trying to figure out the difference between Hard and Soft Fixed, and between Hard and Soft Simple, but I'm not getting it. Have you figured that out?
Eric
Paul,
In the Elmer documentation, I found this description of the boundary conditions available. Do you know the physical meaning of the highlighted parameters? Do you know what the vectors n and t are referring to? I'm trying to figure out the difference between Hard and Soft Fixed, and between Hard and Soft Simple, but I'm not getting it. Have you figured that out?
Eric
Hello Paul,
I made some tests. Thanks a lot for the files! See below the summary of the steps.
What is missing for me at the moment is how to see the geo file (if possible) and get the .msh file (I have problems with gmsh...)
From the .msh to the vtu it works "from the box", the 2D in paraview also. Some mystery remaining around the 3D view.
One question : about the axis in Paraview, is it a view from X to be used as the membrane is in the XY plan (see pic below)?
To be continued.
Here are the details is others want to test
My laptop is under Linux Manjaro (based on Arch)
Were installed from the repositories : Elmer (from AUR repo), Paraview
Then, the file stadium.zip from Paul was unzip in a directory stadiumdir
Content :
cantilever.geo cantilever.msh case.sif ELMERSOLVER_STARTINFO
In this directory, open a terminal then the command line :
* ElmerGrid 14 2 cantilever.msh -autoclean -out mesh
Rem : ElmerGrid not elmergrid (commands are case sensitive)
It generates the mesh in the Elmer format from the .msh file.
New content :
cantilever.geo cantilever.msh case.sif ELMERSOLVER_STARTINFO mesh
A mesh directory was created. Content :
entities.sif mesh.boundary mesh.elements mesh.header mesh.names mesh.nodes
Then the solver is launched (terminal in stadiumdir)
* ElmerSolver
New content :
cantilever.geo case.sif mesh simple.dat.names
cantilever.msh ELMERSOLVER_STARTINFO simple.dat
In mesh :
case_t0001.vtu mesh.boundary mesh.header mesh.nodes
entities.sif mesh.elements mesh.names
Then launch paraview and open case_t0001.vtu (in mesh directory).
H Christian
to view the geo file you can either use a text editor or open in gmsh. There is an option in the tree commands at the left, near the end of geometry section to open the text file. I use it a lot, edit the file and reload, because I find gmsh gui to be unintuitive and clunky. It’s usually easier to write the file by hand, one you have an example of the syntax.
To get the mesh, open the geo file with gmsh and under the mesh commands click first “1” (create 1d mesh on boundaries) then “2” (create 2d mesh). Then do file/save mesh. Or you can use the gmsh command line.
I have set up a minimum mesh size under edit/options … then select the mesh tab. I set minimum to 10, max to 30. If you don’t do this the mesh is to fine and it will lock up the program when you mesh. I specified dimensions in mm, with a conversion to m in the sif file. Alternatively you could work in metres without the conversion. There is an option under file I think to save the options as the default values.
There are some good tutorials about basic gmsh usage on YouTube.
Christian,
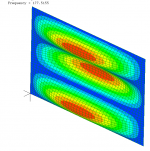
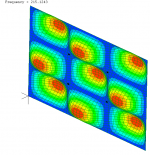
Not always, but in some simple situations, yes, I think the FEM gives a good idea of the FR response and where the peaks will be. For example, below is the FEM result for a hypothetical 4 mm thick plywood panel, 600 mm x 960 mm. The highlighted modes are the productive odd, odd modes as follows:
23 Hz, 1,1 Fundamental
78 Hz 1,3 Mode
177 Hz 3,1 Mode
199 Hz 5,1 Mode
215 Hz 3,3 Mode
314 Hz, 3,5 mode
I would expect the following: Possibly a small peak at the fundamental, but no significant output, as it's just too low. The first real SPL around 1,3 Mode at 78 Hz, then a big dip followed by a nasty spike or spikes around 200 Hz produced by the combination of the 3,1 and 5,1 and 3,3 modes peaking within a small band. Then another big dip until 300 Hz when the 3.5 kicks in.
Eric
Hi christian
With “all else being equal” two close resonances will give a higher peak than one, since we are dealing with a linear system. A large gap between resonances will give a dip. So yes the object is to get as many peaks as possible, as evenly distributed as possible.
Layered on top of this is the problem of unproductive modes, whic are not seen as peaks (at least not in the far field) where cancellation occurs because high and low pressure areas are closer than a wavelength in air, and the air simply moves to equalise the pressure before the wave can get away.
I am hoping to model a driving point force harmonic analysis (rather than just the natural modes) and after that look at helmholz to simulate in air. But I expect the helmholz will be very slow to run on a desktop/laptop. If we had a fast proxy for sound pressure level in the far field, we could do optimisations in a reasonable time eg for location of the exciter. There are approximations in the literature which could be calculated in eg python/scipy. But I would need to understand everything perfectly for that, and that is a goal I’ve not reached 🙂.
No Ive not figured it out or researched further. I'm picturing theta as the angle the plate makes with the equilibrium position at an edge, and n as a normal vector at the edge. And the dot product specifying that the angle must remain 90 degrees? But with those assumptions I cant imagine how the dot product can be other than 0. In summary, dunno. I may ask on the forum. I got a quick response to a really stupid first question yesterday, so if they've not lost their patience with me...
Btw they confirmed that Y and Z results are the derivatives in X and Y direction.
I think there are some clues in the paper. https://iopscience.iop.org/article/10.1088/1757-899X/661/1/012002/pdf
The things I know of which might be controlled at a boundary include
- z position (allow/disallow motion perpendicular to plate at the edge)
- x and y position (allow/disallow motion in-plane. There is something called a 'sliding support').
- Allow/disallow rotation about an edge (or I think equivalently, whether or not the edge is allowed to support a moment about an axis along the edge)
- Allow/disallow shear stress, mentioned in the above paper
- Also the first and second derivative of displacement at the edge. I assumed allowing a first deriv was equivalent to allowing rotation, but Im probably wrong.
Maybe you can make more of this than I. I have not watched any lectures on 3D stress/strain etc.
Hello Christian.
I have been away for a few days in sunny Tewkesbury .
Looking back at your measurements comparing OB with the canvas DML.
they would have similarities in the low end because the canvas and ply panel is very similar to a large BMR .
The canvas and ply panel is very pistonic 😱 in the low end.
It is not purely pistonic but also has bendingwave and DML properties too.
Before I glued the ply panel to the canvas, I measured its response.
There was very little difference in the panels response above its low end roll off frequency, except for a little canvas damping.
But the canvas extended the low end down to 40hz.
But I do not believe this is pure pistonic action.
There is a combination of bendingwave and DML.
So when you measure your canvas panels or other panels , you have to ask yourself which am I measuring?
Hope this clears up some of the confusion of your measurements?
Steve.