Another design I've come up when thinking further on negative impedance converter topologies:
Ignoring the input buffer, this is a 2-stage amp. Standard CFP output stage fed from a bootstrapped opamp implementing a NIC with gain of 20.
The input point at XXX has a -2k impedance, which is why the buffer is added (although it simulates fine without it, if driven from a low impedance).
The -2k is the difference between the R4 and R2, as the non-inverting input is impedance converted to -20k (reflection of R2).
The inputs to the opamp (grey line below) swing at half the output voltage, allowing the overall opamp supply range (cyan/magenta) to swing completely above and below ground:
(There is a 33V zener to define the opamp supply voltage plus decoupling cap)
Square waves are handled fairly well (a little bit of raggedness, hard to see on the 10kHz plot)
I've not tried this for real yet - I suspect it will be fussier in real life than simulated. And it will need a proper bias circuit.
R21/C8 form a snubber needed to shunt any unwanted HF feedback via the bootstrapping path leading to oscillation - the simulation needs it, I suspect this will be somewhat different in reality.
Ignoring the input buffer, this is a 2-stage amp. Standard CFP output stage fed from a bootstrapped opamp implementing a NIC with gain of 20.
The input point at XXX has a -2k impedance, which is why the buffer is added (although it simulates fine without it, if driven from a low impedance).
The -2k is the difference between the R4 and R2, as the non-inverting input is impedance converted to -20k (reflection of R2).
The inputs to the opamp (grey line below) swing at half the output voltage, allowing the overall opamp supply range (cyan/magenta) to swing completely above and below ground:
(There is a 33V zener to define the opamp supply voltage plus decoupling cap)
Square waves are handled fairly well (a little bit of raggedness, hard to see on the 10kHz plot)
I've not tried this for real yet - I suspect it will be fussier in real life than simulated. And it will need a proper bias circuit.
R21/C8 form a snubber needed to shunt any unwanted HF feedback via the bootstrapping path leading to oscillation - the simulation needs it, I suspect this will be somewhat different in reality.
Last edited:
Oh yes, it seems to simulate down to around 0.01%, rising somewhat at high output levels and high frequencies, but performing worst at low output levels due to the sharp cross-over zone of a CFP. This is about what I'd expect from a raw CFP output stage, it is the limiting factor here I believe.
To this date, I don't understand the purpose/advantage of no global feedback amplifiers. Feedback just makes everything better since it minimizes errors, you just need to be careful with stability.
Nothing and I never said it did. But you need 3 stages for that. This is my attempt to design something minimal and novel.
If you want global feedback NIC circuit my other thread is here: NIC opamp VAS topology
Well if you note this is really 2 amplifiers chained together, each using lots of negative feedback. The NIC circuit uses an opamp, the output stage using complementary feedback pairs. Each has issues of stability of its own, but owes its linearity to the feedback. CFP was explicitly selected for this design due to the lack of GNFB.
Global feedback does have downsides, it doesn't make everything better, it makes most things better. For instance this circuit can directly drive 100uF in parallel to 8 ohms without any hint of stability problems (output device SOA problems for sure...)
Last edited:
Well I've breadboarded it using an LM4562, forgot C4 and any ceramic rail capacitors and it seemed stable even so. I didn't bother with the buffer. I cobbled up a Vbe multiplier bootstrapped from the same caps and attached an existing CFP output stage test rig I have:
(without a low impedance to drive it, it locks to one rail, but that's expected)
The square wave performance at 20kHz:
And clipping is civilized (no load):
I did put an 8 ohm load on it, but with only 0.5A supply that limited full power testing.
(without a low impedance to drive it, it locks to one rail, but that's expected)
The square wave performance at 20kHz:
And clipping is civilized (no load):
I did put an 8 ohm load on it, but with only 0.5A supply that limited full power testing.
I am actually curious about this topic. So Global Negative Feedback (GNFB) in my mind has only 1 downside: Stability
Stability has consequences like lower cap drive capabilities and lower speed.
Given the world we live in, namely audio, these consequences don't matter much.
- Speed: audio ends at 20KHz. With modern devices, you can build an audio amp with BW >1MHz without an issue. GNFB will be never be used in RF and wireless though.
- Cap drive: If a Zobel network is used, which decouples the speaker from the amp, there is no need to drive high caps. Let alone 100uF, this is an amp not a regulator. Even then, there are simple techniques to achieve high cap-drive. E.g. the AD826, a 50MHz op-amp, can drive 1nF.
But this stability downside is a small price to pay for the linearization benefits of GNFB. I understand the precense of local feedbacks in the circuit, but usually that is not good enough. The CFP output stage is far from linear, it has a nasty cross-over non-linearity that is not minimized by the absence of GNFB.
So yes, GNFB does not improve stability nor cap drive, but improves everything else.
I think Mlloyd has the spot on answer: "[Without GNFB] the distortion spectrum is different. Some people think that is better."
There is no argument against that.
On a side node, there is an oscillation riding on the square wave. It settles so the circuit is stable, but still there is something weird there.
Global feedback is definitely used for modulation envelopes in RF though, because that has lower bandwidth than a carrier its quite feasible. Its one of several ways to get efficient RF amplifiers linear enough for complex QAM codings and the like. You need to reduce intermodulation distortion within the signal band (out-of band harmonics are trivial to remove, so harmonic distortion per-se is irrelevant)
Oddly the breadboard seemed less prone to oscillation than the simulation was, but that might partly be not having a proper LM4562 spice model.
Yes, and for at least two reasons, firstly I noted this in the simulation, couldn't really eliminate it which is what I was getting at with my comment:
Also I forgot the snubber on the breadboard for the opamp rails, so that's probably made it worse. Will bring this up again and fiddle with it at some point.
Oddly the breadboard seemed less prone to oscillation than the simulation was, but that might partly be not having a proper LM4562 spice model.
Breadboards also have 2-10pF inter line capacitance depending on the size and quality of the breadboards. Maybe there is something because of that too, but I am only guessing here [Shooting a dart to the sky =)].
Perhaps I was lucky with the layout I chose? The problem then is designing a pcb and knowing if it will be similarly lucky.
Sandro, there are some ways to make step response mostly like a perfect aperiodic function even with a high-order compensation.
Let's name this gain-shaping.
Since step response is analytically related with freq-response through integral/derivative and FFT/iFFT we always can change pole-zero relation in feedbacked system and achieve fairly aperiodic response, something like attached. Sorry for image quality.
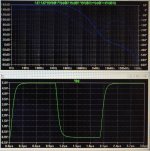
Hi Pavel, not sure sure what is your point or what you are trying to get at.
Your picture shows the open loop gain of a two-pole system/amplifier and its associated step response. Since you have a ton of phase margin and gain margin, it is very stable.
Your picture shows the open loop gain of a two-pole system/amplifier and its associated step response. Since you have a ton of phase margin and gain margin, it is very stable.
Oh, no, please check dotted phase line, it's fall down to 300 degree around 1meg.
Yes, there are a tons of margins because of need to further optimizing with accounting board/elements parasitics.
My point is a possibility of analytical solving pole-zero frequencies for providing smooth like-1-order step-response of high-order systems.
There is, it is called Phase Margin and Gain margin which are adjusted via moving pole and zero frequencies. There is a relationship between overshoot and phase margin. In practice Phase margin > 75, provided gain margin is ~10dB or higher, yield 1st order responses.
Look at: YouTube
Scroll to minte 14:22 for a plot.
Since I am sure you already knew this, I am still not sure what you are getting at.
The worst kinds of instability are non-linear and/or chaotic, here's an example I've encountered playing with boot-strapped opamp circuits (it basically worked but with low-amplitude HF chaotic oscillations riding on top of the main signal):
Non linear behaviour is, I suspect, all too common in circuitry we analyze using linear models.
Non linear behaviour is, I suspect, all too common in circuitry we analyze using linear models.
Hi Mark
Try adding 100nF rail-to-rail on the floating supply. I had some noise appear only at low output levels in a similar situ and the cap fixed it. large signal performance was not effected.
Try adding 100nF rail-to-rail on the floating supply. I had some noise appear only at low output levels in a similar situ and the cap fixed it. large signal performance was not effected.
Hey
I didn't see C1 as the schemo is a little messy. I saw the bootstrap caps for the floating supply and immediately thought "missing 100nF".
But your floating supply looks strange to me. Normally there are two zeners, one each across the two bootstrap caps to assure that there is something approaching symmetric drive on both halves of the wave - your waveforms look like there is anyway. The resistors in series with the 47uFs seems problematic. Why are they there? These changes might allow removal of the bandaid from the negative opamp supply pin.
I didn't see C1 as the schemo is a little messy. I saw the bootstrap caps for the floating supply and immediately thought "missing 100nF".
But your floating supply looks strange to me. Normally there are two zeners, one each across the two bootstrap caps to assure that there is something approaching symmetric drive on both halves of the wave - your waveforms look like there is anyway. The resistors in series with the 47uFs seems problematic. Why are they there? These changes might allow removal of the bandaid from the negative opamp supply pin.