line arrays
re' which I expanded your example to 24 drivers and everything was fine; then added a driver and got access violation at address 00515BC1
Last edited:
line arrays... should've seen that.
Can you zip up the file (before adding the crashing step) and send or post it?
Can you zip up the file (before adding the crashing step) and send or post it?
Havent got to your file, but wondering --is this a LA youve built? If, so great test case to compare with reality!
You mention you are pre-diffraction at this point. Couldn't you use an absolute distance value for phase?
I probably was a little too quick to pull the trigger on my response WRT complex interpolation. In what I read as follow-up, the trend I'm noticing is that folks will split the arrays into their real and imaginary components (or polar, take your pick) and do the interpolation of the two arrays separately.
Not sure how badly that would screw up magnitudes, though.
E.g python - Interpolate whole arrays of complex numbers - Stack Overflow albeit this discussion is for Numpy, same concept.
E.g. (2) This is how Matlab's baked in interpolation does it, too http://www.mathworks.com/help/matlab/ref/interp1.html#btw0gu1-1
Last edited:
DPH, thanks.
Actually, I already do something like that for interpolation over frequency. I used a "constrained spline" curve fit to map from one set of frequency points to another. In the sim I always work with the same set of frequency points, so when data is read in from any-old FRD file, the first thing that happens is to map it to my working frequency list. I usually interpolate real and imaginary (separately), since that sidesteps the issue of unwrapping phase being somewhat error prone. But I guess there's no reason such an interpolation wouldn't work for points spaced geometrically. But it still doesn't solve my issue of how to combine data taken at horizontal offsets with data taken at vertical offsets.
My test case (a circular piston, where I can calculate response vs an angle "theta" relative to the disk's normal vector) lets me calculate a usable value, and also I can calculate responses from vertical and horizontal offset angles-only values separately so I can check how well various combining approaches work (ideally, the result would be the same using the overall 'theta' value.
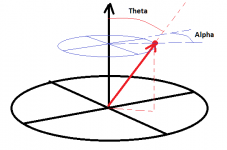
I haven't gotten too far into it today (other matters call) but it occurred to me this morning that I should perhaps convert the measured data arrays so the they are mapped, instead of in Horizontal and Vertical angles, into something more "circularly" oriented, see diagram below -
Attachments
Last edited:
Sure there is, I do it all the time. All you have to do actually is to take any real interpolation algorithm and make the variables complex. In FORTRAN this is trivial, in other languages not so much since only FORTRAN has a complex data type and keeps track of all the complexities for you. The only "gotcha" is that if you ever need to multiply two complex numbers then "usually" you have to multiple one as a conjugate.
I have a FORTRAN routine that will do this that I could send you.
Thanks, Earl. I already put together a set of complex math routines the language I use (Delphi, a graphical version of Object Pascal), so I have that pretty well covered. I guess my issue wasn't so much doing a spline interpolation (which I'm doing already for frequency-indexed values) but instead how to do it for something indexed in terms of H and V. I think I might see how to approach that now (see my pic a few posts up), if I arrange the data I index against a little differently. Or maybe not, I have to sit down with some coffee and scratch my head a bit...
I think the trick might be to first interpolate my measured data sets to get H and V values first at the same "theta" angle as the desired orientation, then interpolate between those using the Alpha value...?
Bill
As I understand what you want to do, I think that it cannot be done the way that you want. I do much like what you are suggesting and Klippel does exactly what I think you want, but we both do it in spherical coordinates. In that system what you want to do falls out naturally, but in half space, polar coordinates, I think that it is a problem, especially if you then want to go into rectangular coordinates with circular symmetry. It just gets messy.
In spherical you simply define a sphere about your speaker and expand the radiation in the radiation modes of Spherical Bessel Functions and Associated Legendre Polynomials. You can then add or subtract any number of sources in this new modal description and rotate them or whatever you want to do.
That's how I do my measurement system, but only for horizontal measurements. Klippel does the full 3D model. This allows for any level of complexity of the source, but you do then need to be careful of how many modes you use and to what frequency (ka value) or the solution will not converge. There is also a LF singularity that you need to be careful of, but this is the only way that I know of to do this problem.
This was first shown by Weinreich at the University of Michigan back in the 50's, and published in JASA. I did it back in the early 2000's and Klippel has recently redone it (I was disappointed to see that he made no reference to all of the prior art on this.)
As I understand what you want to do, I think that it cannot be done the way that you want. I do much like what you are suggesting and Klippel does exactly what I think you want, but we both do it in spherical coordinates. In that system what you want to do falls out naturally, but in half space, polar coordinates, I think that it is a problem, especially if you then want to go into rectangular coordinates with circular symmetry. It just gets messy.
In spherical you simply define a sphere about your speaker and expand the radiation in the radiation modes of Spherical Bessel Functions and Associated Legendre Polynomials. You can then add or subtract any number of sources in this new modal description and rotate them or whatever you want to do.
That's how I do my measurement system, but only for horizontal measurements. Klippel does the full 3D model. This allows for any level of complexity of the source, but you do then need to be careful of how many modes you use and to what frequency (ka value) or the solution will not converge. There is also a LF singularity that you need to be careful of, but this is the only way that I know of to do this problem.
This was first shown by Weinreich at the University of Michigan back in the 50's, and published in JASA. I did it back in the early 2000's and Klippel has recently redone it (I was disappointed to see that he made no reference to all of the prior art on this.)
Thanks Earl, I'll ponder on that (some googling required to understand).
Is the diagram I sketched just above spherical coordinates?
Is the diagram I sketched just above spherical coordinates?
I didn't know that Delphi was still available. I tend to work in VB.Net which has a vast array of abilities. I can barely touch the surface.
Delphi is still around (but very expensive now -- I still use the Delphi 5 installation from 1999!). I tried VB back then and absolutely hated it, very unintuitive at least to me, seemed like it had been designed by a bunch of guys who couldn't agree with each other!. But that might've just been because I'd been programming in Pascal for a while already so was used to it. I also like how Delphi compiles to fast raw object ccode in about 2 seconds, while the other compilers seem to take forever.
VB.Net is when the language really got good. That's when all of MS languages converged on the .Net platform with a common set of routines. Visual Studio is the best development platform that I have ever used and the fact that it can compile code written in VB, C#, C++, F#, FORTRAN, etc. makes it very flexible. It can use all these languages within a single app - use whatever language best suites the situation. I have written apps using VB, C++ and FORTRAN all in the same workspace and exe.
Looks like what I sketched above is indeed spherical coordinates (with non-accepted names for the coordinates themselves). I think I need to do a little reading to avoid trying to reinvent any wheels.
Yes, R, Theta and Phi, are the standard spherical coordinates. In what you have defined, theta cannot be periodic with Pi, (the infinite plane means that +-PI/2 are the limits) which would require you to redefine the whole set of functions (I wouldn't suggest that you do that!). If you let theta go to +-PI then all the functions have been defined and are available in most software packages - I have them all in FORTRAN. Its just a matter of organizing the analysis using these predefined functions.
Whatever you do, I suspect that you will need to expand the radiation into a set of orthogonal functions, of which your simple disk is but one. This works fine for the unique situation of a rigid disk, but the minute you deviate from this simplicity that sole function will no longer suffice. You can always define the set of functions that you want to work with, but that is the hard way to go.
I can tell you how to do all of this, but this forum is not conducive to detailed discussions like that. Its too hard to write the math. Read Winreichs paper will help, but be for-warned that he uses very Physics oriented language which will be very different for a EE.
- Status
- Not open for further replies.