Hello all,
Building some ladder attenuators (24 step) for the value amp, have the resistor values (Rx and Ry) for the 100K log LADDER attenuator, but struggling to find the Rx and Ry values for a 1M linear (to use on the tone controls)
Any cheat sheets out there?
Malcolm
Building some ladder attenuators (24 step) for the value amp, have the resistor values (Rx and Ry) for the 100K log LADDER attenuator, but struggling to find the Rx and Ry values for a 1M linear (to use on the tone controls)
Any cheat sheets out there?
Malcolm
24 positions means 23 resistors. Linear means all-equal.
1,000,000 Ohms / 23 = 43,478 Ohms.
43,200 is a Standard Value in E96 (1%).
43,000 is a Standard Value in E24 (5%).
Buy twenty-three for mono, forty-six for stereo.
NOTE that a 24-position switch will not naturally have a "center position". The alternative is to strap two poles on one end, work it as a 23 position, and buy 22 (or 44) 45,454 Ohm resistors.
1,000,000 Ohms / 23 = 43,478 Ohms.
43,200 is a Standard Value in E96 (1%).
43,000 is a Standard Value in E24 (5%).
Buy twenty-three for mono, forty-six for stereo.
NOTE that a 24-position switch will not naturally have a "center position". The alternative is to strap two poles on one end, work it as a 23 position, and buy 22 (or 44) 45,454 Ohm resistors.
Last edited:
Thanks PRR, but if I put 43,200 into Rx Ry on a 24 throw Ladder Attenuator I would wind up with a constant 1/23 of the tone control!
Your calculations are correct for a 24 throw SERIES attenuator, but not a LADDER attenuator.
Thanks anyway for the quick reply....all the best.
Your calculations are correct for a 24 throw SERIES attenuator, but not a LADDER attenuator.
Thanks anyway for the quick reply....all the best.
Last edited:
Does Fig. 2 show what you call a ladder attenuator? Then you also can use PRR's calculation: The upmost pair gets values of 43k2 on the left hand and (23 x 43k2=) 993k6 on the right hand side, the 2nd pair 2 x 43k2 and 22 x 43k2 etc., until you end with 23 x 43k2 and 43k2 for the pair at the bottom.
Best regards!
Best regards!
Last edited:
Ah, difference in variation of the input and output impedance?
Both are the same as in each voltage divider type attenuator with the same total resistance value.
the calculator you opened shows series and shunt.Thanks jazbo8, the site has a calculator for series and shunt, can the shunt calculator be used for Ladder (parallel)?
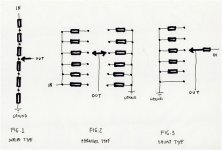
My understanding is that they are different, see attached.
View attachment 605058
Can't you see that series is your FIG. 1 and shunt is your FIG. 3?
Why do you want/need a linear law?
Why do you want/need "ladder" type?
Do you know why you want/need those?
Do you know what they offer that is an advantage over other types?
Maybe because he wants to build an active Baxandall type tone control?Why do you want/need a linear law?
Why do you want/need "ladder" type?
Do you know why you want/need those?
Do you know what they offer that is an advantage over other types?
These points also aren't easy to follow for me.
Best regards!
Thanks all and to close this off.
Firstly, my apologies PPR, your calculation was right I was just confused when you said buy 23 resistors.
Kay your responce makes sense so will build a protype and see how it goes!
Scotjplin, series attenuators put the resistors in series so as you go up the stack, each resistor adds more noise to the circuit and this is compounding. Although ladder are more complex they do have a better result, which is why most volume attenuators (log) use this configuration.
Happy days, will let you know how it goes!
Firstly, my apologies PPR, your calculation was right I was just confused when you said buy 23 resistors.
Kay your responce makes sense so will build a protype and see how it goes!
Scotjplin, series attenuators put the resistors in series so as you go up the stack, each resistor adds more noise to the circuit and this is compounding. Although ladder are more complex they do have a better result, which is why most volume attenuators (log) use this configuration.
Happy days, will let you know how it goes!
the noise you refer to is dependant on the resistance...............series attenuators put the resistors in series so as you go up the stack, each resistor adds more noise to the circuit and this is compounding. Although ladder are more complex they do have a better result, which is why most volume attenuators (log) use this configuration..............
If you have a 10k resistor it has the same noise as 10off 1k resistors.
Put a vol pot in there with a 10k resistance and it has the same effect as the two resistors that would be above and below the wiper that add up to that 10k
A vol pot whether linear or log law generates the same noise when they are both attenuating by the same amount.
A series switcher and a ladder switcher have exactly the same effect on the noise they each create.
If all of the above were of metal type then all would have the same noise.
A carbon track vol pot will have more noise than any of the metal types.
I suspect a plastic type resistive track will have some intermediate noise level compared to metal & carbon.
Last edited:
the noise you refer to is dependant on the resistance.
If you have a 10k resistor it has the same noise as 10off 1k resistors.
That figures, the Johnson noise, dependant only on total resistance? It looked from jazbo's link that may be difference in impedance that is all
Last edited:
Correct on the impedence and here an interesting link to a missive https://www.blackdahlia.com/html/tip_67.html
Here's what you are looking for, for 'ladder' resistor setup:
Call R1 the "input" resistor
Call R2 the "output" resistor.
If Linear, 24 steps from 100% to 0%:
STEP ATTN-RATIO R1 R2
0 0.00% - 100.00
1 4.35% 4.35 95.65
2 8.70% 8.70 91.30
3 13.04% 13.04 86.96
4 17.39% 17.39 82.61
5 21.74% 21.74 78.26
6 26.09% 26.09 73.91
7 30.43% 30.43 69.57
8 34.78% 34.78 65.22
9 39.13% 39.13 60.87
10 43.48% 43.48 56.52
11 47.83% 47.83 52.17
12 52.17% 52.17 47.83
13 56.52% 56.52 43.48
14 60.87% 60.87 39.13
15 65.22% 65.22 34.78
16 69.57% 69.57 30.43
17 73.91% 73.91 26.09
18 78.26% 78.26 21.74
19 82.61% 82.61 17.39
20 86.96% 86.96 13.04
21 91.30% 91.30 8.70
22 95.65% 95.65 4.35
23 100.00% 100.00 -
Essentially R1 + R2 ≡ 100 kΩ (say)
To get the attenuation, R1 = 100 kΩ • ratio.
Then, 100 kΩ - R1 is R2
Not at all very difficult, really. Indeed, this is also the easiest way to compute log scale divider stacks. For the same "100 K input impedance" you'd just have:
dB RATIO R1 R2
0 0.00% - 100,000.00
-3 29.21% 29,205.00 70,795.00
-6 49.88% 49,881.00 50,119.00
-9 64.52% 64,519.00 35,481.00
-12 74.88% 74,881.00 25,119.00
-15 82.22% 82,217.00 17,783.00
-18 87.41% 87,411.00 12,589.00
-21 91.09% 91,087.00 8,913.00
-24 93.69% 93,690.00 6,310.00
-27 95.53% 95,533.00 4,467.00
-30 96.84% 96,838.00 3,162.00
-33 97.76% 97,761.00 2,239.00
-36 98.42% 98,415.00 1,585.00
-39 98.88% 98,878.00 1,122.00
-42 99.21% 99,206.00 794.00
-45 99.44% 99,438.00 562.00
-48 99.60% 99,602.00 398.00
-51 99.72% 99,718.00 282.00
-54 99.80% 99,800.00 200.00
-57 99.86% 99,859.00 141.00
-60 99.90% 99,900.00 100.00
-63 99.93% 99,929.00 71.00
-66 99.95% 99,950.00 50.00
-69 99.96% 99,965.00 35.00
So, there you be.
GoatGuy
Call R1 the "input" resistor
Call R2 the "output" resistor.
If Linear, 24 steps from 100% to 0%:
STEP ATTN-RATIO R1 R2
0 0.00% - 100.00
1 4.35% 4.35 95.65
2 8.70% 8.70 91.30
3 13.04% 13.04 86.96
4 17.39% 17.39 82.61
5 21.74% 21.74 78.26
6 26.09% 26.09 73.91
7 30.43% 30.43 69.57
8 34.78% 34.78 65.22
9 39.13% 39.13 60.87
10 43.48% 43.48 56.52
11 47.83% 47.83 52.17
12 52.17% 52.17 47.83
13 56.52% 56.52 43.48
14 60.87% 60.87 39.13
15 65.22% 65.22 34.78
16 69.57% 69.57 30.43
17 73.91% 73.91 26.09
18 78.26% 78.26 21.74
19 82.61% 82.61 17.39
20 86.96% 86.96 13.04
21 91.30% 91.30 8.70
22 95.65% 95.65 4.35
23 100.00% 100.00 -
Essentially R1 + R2 ≡ 100 kΩ (say)
To get the attenuation, R1 = 100 kΩ • ratio.
Then, 100 kΩ - R1 is R2
Not at all very difficult, really. Indeed, this is also the easiest way to compute log scale divider stacks. For the same "100 K input impedance" you'd just have:
dB RATIO R1 R2
0 0.00% - 100,000.00
-3 29.21% 29,205.00 70,795.00
-6 49.88% 49,881.00 50,119.00
-9 64.52% 64,519.00 35,481.00
-12 74.88% 74,881.00 25,119.00
-15 82.22% 82,217.00 17,783.00
-18 87.41% 87,411.00 12,589.00
-21 91.09% 91,087.00 8,913.00
-24 93.69% 93,690.00 6,310.00
-27 95.53% 95,533.00 4,467.00
-30 96.84% 96,838.00 3,162.00
-33 97.76% 97,761.00 2,239.00
-36 98.42% 98,415.00 1,585.00
-39 98.88% 98,878.00 1,122.00
-42 99.21% 99,206.00 794.00
-45 99.44% 99,438.00 562.00
-48 99.60% 99,602.00 398.00
-51 99.72% 99,718.00 282.00
-54 99.80% 99,800.00 200.00
-57 99.86% 99,859.00 141.00
-60 99.90% 99,900.00 100.00
-63 99.93% 99,929.00 71.00
-66 99.95% 99,950.00 50.00
-69 99.96% 99,965.00 35.00
So, there you be.
GoatGuy
Last edited:
- Home
- Design & Build
- Parts
- Resistor Values for LINEAR Ladder Attenuator (not series Attenuator)