I personally thought that file A sounded a little rounder or warmer, whereas B did not. I assumed that this was due to the addition of more second harmonics and figured this would make sense given how SE class A tubes are supposed to sound.
Maybe the addition of the extra high frequency content over the fundamentals actually made things sound thinner instead.
Maybe the addition of the extra high frequency content over the fundamentals actually made things sound thinner instead.
IME, the sound of distortion changes with the register. A good dose of 3rd HD in the bass sounds fat and pleasing. Midrange and above it does not. Just a simple example, but surely there has been much published on the subject.
On the first test 440/880 at a 10:1 ratio I can hear two distinctive tones just as well as I can with 440/880 at a 1:1 ratio.
The second test is far to complex to distinguish separate tones and seems more a matter timbre. I've never thought about a square sounding like a clarinet but now that you have mentioned it... A clarinet sounds so much nicer.
The problem is Frank, better cd sounds much better now. I mean, why not all sound terrible using the same amp and chain. I know this is surprising. We have heard this phenomenon existence but rarely we experience it first hand. Better chain only improve better recording dramatically.
Jay, overall I've found this an iterative process - depending upon precisely what weaknesses have been addressed at a particular point in time, certain recordings will sound much better and others will seem to fall behind. One touchstone is that if the speaker drivers, and crossovers are of very high quality then relatively simple recordings, which emphasise the "beauty" of individual notes from one or two instruments, with extremely spare production, will do very nicely. "Congested" recordings may still sound messy in this situation, but this is a problem further back in the chain - the unpleasantness now has nothing to do with the speakers, but is electronics misbehaving.
I've always worked on unscrambling very thick, dense recordings - because if you get this right then everything becomes listenable to, is always a pleasure. Flaws here originate from electronics not working optimally - and once that's debugged then one can move forward in improving the purity of clear tones, by using better speakers, say.
This is a technique that I've developed and refined over many, many years, and it has always worked - I always end up getting recordings that I know well to sound the same, meaning that I've got to the heart of captured material. In the normal measurement sense the systems would all vary wildly, but as far as the listening is concerned that doesn't matter - the remaining weaknesses are no longer subjectively audible.
Having a system sound brilliant on some material, and dreadful on the next is disasterous - I've heard this too many times, and it's a dead end. I think here of an ulta-expensive, ultra-ambitious system assembled for a demo - put on a percussion piece, that I didn't know, veeerry spectacular. Then, a Sinatra CD - terrible !!! The sound was so lopsided, only exactly the 'right' music was playable on it ...
I've always worked on unscrambling very thick, dense recordings - because if you get this right then everything becomes listenable to, is always a pleasure. Flaws here originate from electronics not working optimally - and once that's debugged then one can move forward in improving the purity of clear tones, by using better speakers, say.
This is a technique that I've developed and refined over many, many years, and it has always worked - I always end up getting recordings that I know well to sound the same, meaning that I've got to the heart of captured material. In the normal measurement sense the systems would all vary wildly, but as far as the listening is concerned that doesn't matter - the remaining weaknesses are no longer subjectively audible.
Having a system sound brilliant on some material, and dreadful on the next is disasterous - I've heard this too many times, and it's a dead end. I think here of an ulta-expensive, ultra-ambitious system assembled for a demo - put on a percussion piece, that I didn't know, veeerry spectacular. Then, a Sinatra CD - terrible !!! The sound was so lopsided, only exactly the 'right' music was playable on it ...
It's only "second harmonic distortion" with a sine wave input. If there's more than one sine wave, as there certainly are in this sound file, there's also intermodulation distortion (see second plot in post #24), and offhand I don't think it's possible to separate the two, so it's hard to say which one has how much influence to the sound.
What I was seeing here was that 04b has a cut-off spectrum between about 20.5k and 22k, whereas 04a doesn't:. Here's the "Frequency Analysis" window of 04a from Cool Edit at 20.419 seconds:
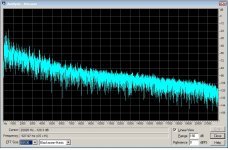
And likewise for 04b:
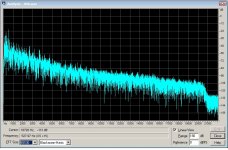
This dropoff is surely inaudible to most if not everyone, and regardless, is swamped by the lower frequencies, even presuming one's hearing goes over 20k.
I don't know what causes that (I'm guessing the polynomial eval routine upsamples, does its thing, then filters to below 22k before downsampling), but from it I determined that 04b was constructed from the "original" 04a. Perhaps if you generated a "purely linear" transfer with the polynomial eval routine, you'd get the undistorted file but with that same dropoff.
The dynamics are practically identical - the levels of the fundamentals are probaby the same within 0.01dB, though the added harmonics and IM signals might add another few 0.01dBs.
But the audible or percieved dynamics might be significantly more, since the ear hears all these added tones as the sound being louder. And since the distortion is higher with increased signal level, the loud portions are made disproportioally louder, than the soft portions.
I remember reading some US audio/stereo/hifi magazine article, in the late 1970s, about this Aphex thing that had come out a few year before, and was used on the vocals of many popular recordings:
https://en.wikipedia.org/wiki/Exciter_%28effect%29
The author of the article was up in arms about recording studios INTENTIONALLY adding distortion to recorded music!
Last edited:
The fundamental and second harmonic are usually easy to hear as separate tones, especially if you first hear individually the fundamental and then the harmonic - the combined tone is then obviously the combination of the two sine waves, and you "remember" the 2nd being an individual tone.
The more harmonics a "tone" has, the harder it is to recognize specific harmonics. It starts to sound like a single tone with a different timbre as the harmonics are increased or decreased in level.
A Hammond organ with its drawbars is a good tool for learning about perceived harmonic tones vs. perceived timbre. If you hold down a note and move one or more drawbars in or out, you can hear the harmonic tones being added and taken away, but if you play melodies and chords, it sounds like fundamental tones with timber based on the harmonic levels. You can pull out just the odd harmonics (3rd, 5th and 9th, there's no 7th because it's "unmusical") and get that reedy/hollow sound like a square wave.
A clarinet has that "reedy, hollow" sound of a square wave, but it sounds much nicer because it has a wooden body that filters the tone source.
Frank, the speaker is very capable of playing complex music. That's its strength. With bad recording, the sound is not fatiguing and the like, it's just like you can feel the "ladder" of low resolution signal, or certain freq is boosted to improve the vocal, or strangely missing lows (this one I don't understand why)
I don't get what you mean by the "ladder" of low resolution, Jay, this sounds a bit like Richard Marsh's complaints about 16 bit sound, 😉 ! I have only one recording where I can hear a ladder, which is straight out faulty: a CBS opera CD, mastered at an extremely low level, and the dithering at the start was mucked by the engineer. Otherwise, other recordings always reveal more detail the better the system replay gets, I can hear deeper, and further into the sound, more subtle aspects of the recording environment, and the behaviour of the musicians can be picked up; the recording keeps making more and more musical sense, no matter how nominally "poor" it is.
In the files that I posted, distortion is easiest to hear at loud cello bow sound. One can find the distortion in the difference file I posted (by listening), read the time from beginning of the file, and then try to find it at the same part of 04b file. It is audible.
Being a symmetrical distribution it is at it is, but it only means that the _probability_ equals. What somebody will consider as _significant_ is a different question.
What you´ve described would be considered (as Leventhal back in the 80s called it) as statistical significant poor performance, that should lead to another clarification if the participant misunderstood something.
As Pavel asked for preference a two tailed test would be appropriate as their is no real correct response and an ABX-test would not be the "first" choice.
Possibly. or, more likely, the results of the statistical nature of randomness (i.e., no difference is heard). That's why one has to be careful evaluating group tests, as well as individual tests that fall below a reasonable statistical significance. In a group of 100 people, it is almost assured that even when there's no difference, someone will score well. If the test is repeated, someone will again score well, but it's highly unlikely that it will be the same person!
With Pavel's clue on what to listen for, Mooly might score significantly on his ABX test.
Read again what SY was saying. 100 people, no difference, almost assured someone will score well.
When we use logic, isn't it all about Statistics?
It's like saying a million (SQUARED that a thousand times) monkeys hitting a piano, at least one monkey will create a great song 😀
A common criterion for a positive result (means "scoring well" aka rejection of the null hypothesis) is SL=0.05, that means the experimenter would accept that the result was not due to random guessing if the probability to get the result by random guessing will be <5% .
In a 8 trial experiment to get lower than 5% means to get at least 7 hits and the actual probability to get >=7 hits by random guessing is p=0.03125 .
So "scoring well" is to get >= 7 hits and p=0.03125 (by random guessing)
Not "scoring well" means always getting <7 hits (by random guessing)
If you got 100 tests (100 listeners doing the 8 trial experiment) and all were just guessing than the probability that _no_ listener will "score well" by chance is:
1 - P(scoring well)*100 <=> 1 - P(X<7)*100 = (1 - 0.03125)*100 = 0.9633*100 = 0.0418
So the probability that at least one listener will "score well" although _all_ listeners were just guessing would be 96,88% .
Last edited:
yup infinite number of monkeys on infinite number of typewriters will eventually write all the great books.
I have 4 daughters. The chance I will have a 5th in 10 weeks is still 50%. statistics, gotta love em.
I have 4 daughters. The chance I will have a 5th in 10 weeks is still 50%. statistics, gotta love em.
- Status
- Not open for further replies.