Low Distortion DDS based dual channel audio synthesiser
Posted 24th December 2013 at 02:40 AM by googlyone
Well now I am on holidays over XMAS I got the time to really put in a solid chunk of time on the DDS based synthesiser.
Previous blog entries describe the PIC32MX based core to this. The thing works like a charm...
To get decent precision on the sinewave I have implemented an interpolation on a high precision Sinewave lookup table.
- The DDS references into a 12 bit "long", 24 bit "amplitude" precision sinewave LUT.
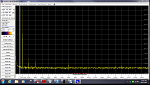
- Of itself this gives mediocre spurs, which in a DDS are heavily dependent on the frequency, but seem to result in 85-90dBc spurs. There is a fair hash of these without treatment.
- By adding a linear interpolation between samples in the Sinewave Lookup table, the spurs come out as shown below...
- The interpolation is actually quite simple in concept:
- The top 12 bits of the DDS Phase Accumulator looks up the "Sine Sample"
- The slope of the waveform is calculated by (Next_Sine_Sample - Current_Sine_Sample)/Sample_Period
- This is scaled up by the remainder (the bottom 20 bits of DDS phase accumulator) and added to the amplitude output.
The measurement shown above was made with my simple external Soudbaster sound card (which does have a 24 bit ADC, but god knows what it's own performance is).
Also the DAC used was one of my CS4398 DAC boards, which uses the OEM reference design for filtering and a NE5532. So again, the performance of the DAC is in the ballpark of the measurement.
Oh, and for the measurement the DDS was set to 10dB attenuation - implemented digitally. So the poor CS4398 was running 10dB below fill scale.....
What do I take from this?
- The DDS, DAC and ADC in the test are generating and measuring a pretty damn clean sinewave.
- The DDS algorithm has successfully abolished the majority of the hash you get from amplitude and time errors
- There is a residual harmonic (2nd) at about -98dBc
- There is a 3rd, 8th and 16th harmonic that are < -100dBc.
I am damned if I could say where these products are originating - DDS, ADC or DAC.
I am pretty chuffed with this!!!
The Synth is also happily doing the following:
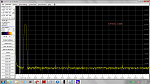
- Frequency Sweeps - same analogue performance, all phase continuous, updated frequency every sample interval
- Amplitude control (I limited this to 48dB in 0.5dB steps because I am lazy) - this will affect the performance too....
- Pulse modulation. 1-1000 cycles on, 1-1000 cycles off, neatly switching at the start of each cycle. Unless you use Phase offset...
- Phase offset per channel. 0-360 degrees in 0.1 degree steps.
- Sine, Triangle, Square, Pulse (1-99% duty cycle) and random noise as waveforms. Each uses 4096 samples per waveform cycle.
- Amplitude modulation. 0-100%, frequency 1-1000Hz
- Frequency modulation. 0-1000Hz peak modulation, 1-1000Hz FM rate (watch those limits)
Sweep running:
Oh, and there are 2 channels (left and right) each independent of the other. I am pretty chuffed with this. Will try slinging it into a box and see how it measures when it is not draped on the workbench.
Previous blog entries describe the PIC32MX based core to this. The thing works like a charm...
To get decent precision on the sinewave I have implemented an interpolation on a high precision Sinewave lookup table.
- The DDS references into a 12 bit "long", 24 bit "amplitude" precision sinewave LUT.
- Of itself this gives mediocre spurs, which in a DDS are heavily dependent on the frequency, but seem to result in 85-90dBc spurs. There is a fair hash of these without treatment.
- By adding a linear interpolation between samples in the Sinewave Lookup table, the spurs come out as shown below...
- The interpolation is actually quite simple in concept:
- The top 12 bits of the DDS Phase Accumulator looks up the "Sine Sample"
- The slope of the waveform is calculated by (Next_Sine_Sample - Current_Sine_Sample)/Sample_Period
- This is scaled up by the remainder (the bottom 20 bits of DDS phase accumulator) and added to the amplitude output.
The measurement shown above was made with my simple external Soudbaster sound card (which does have a 24 bit ADC, but god knows what it's own performance is).
Also the DAC used was one of my CS4398 DAC boards, which uses the OEM reference design for filtering and a NE5532. So again, the performance of the DAC is in the ballpark of the measurement.
Oh, and for the measurement the DDS was set to 10dB attenuation - implemented digitally. So the poor CS4398 was running 10dB below fill scale.....
What do I take from this?
- The DDS, DAC and ADC in the test are generating and measuring a pretty damn clean sinewave.
- The DDS algorithm has successfully abolished the majority of the hash you get from amplitude and time errors
- There is a residual harmonic (2nd) at about -98dBc
- There is a 3rd, 8th and 16th harmonic that are < -100dBc.
I am damned if I could say where these products are originating - DDS, ADC or DAC.
I am pretty chuffed with this!!!
The Synth is also happily doing the following:
- Frequency Sweeps - same analogue performance, all phase continuous, updated frequency every sample interval
- Amplitude control (I limited this to 48dB in 0.5dB steps because I am lazy) - this will affect the performance too....
- Pulse modulation. 1-1000 cycles on, 1-1000 cycles off, neatly switching at the start of each cycle. Unless you use Phase offset...
- Phase offset per channel. 0-360 degrees in 0.1 degree steps.
- Sine, Triangle, Square, Pulse (1-99% duty cycle) and random noise as waveforms. Each uses 4096 samples per waveform cycle.
- Amplitude modulation. 0-100%, frequency 1-1000Hz
- Frequency modulation. 0-1000Hz peak modulation, 1-1000Hz FM rate (watch those limits)
Sweep running:
Oh, and there are 2 channels (left and right) each independent of the other. I am pretty chuffed with this. Will try slinging it into a box and see how it measures when it is not draped on the workbench.
Total Comments 9
Comments
-
Looks like great progress there!
A couple of questions - what's the effective bandwidth in the FFT plot where you show the spurs? Second - can this be adapted to produce a multitone signal? Something like is used to characterize ADSL drivers (e..g AD8016) - 255 discrete tones. My hypothesis is that such a signal as stimulus will achieve better correlation with subjective sound quality than a single sine.Posted 25th December 2013 at 03:12 AM by abraxalito
-
The bandwidth of the FFT plot is limited by the sound card - notionally 24kHz, based on the fact that the card was set up for 48ksps.
I just reset it to 96ksps, which is its limit, and got essentially the same plot.
FWIW, I played last night with tweaking the DDS rate. Without optimising the code effeciency in the Interrupt Service Routine I was able to reduce the I2S divider to "3" which produces 62.5 ks/s output sample rate. There was no obvious effect on distortion products, though I dod not go into gory measurement detail.
So: on the effective frequency resolution of the plot:
- I dont know what the preselection filters are like in the soundblaster X-Fi ADC. I believe it uses a CS delta sigma digitiser that provides a level of filtering itself.
- At a sample rate of 48 and 96ksps, the nyquist answer is simple - perhaps the truth less obvious.
The output could easily be adapted to produce a multitone signal - within limits.
- The implementation I have here actually has:
- A dds for left
- A DDS for right
- A DDS for AM left
- A DDS for AM right
- A DDS for FM left
- A DDS for FM right
There would be no problem at all running these DDS's and "mixing the output together" which is a simple addition.
If you used the standard long integers (+/-31 bits) and kept your scaling sensible you could do that in very few cycles.
If you needed to use 64bit values and (I am not sure this would actually be essential) it would be more expensive, but not a big deal.
If you really wanted heaps of tones, then you would be better off looking for an alternate approach.
If you wanted harmonics, then you could do some clever stuff with the waveform definition. For example a waveform definition that includes multiple even harmonics could quite simply be calculated. Note however that to change the relative magnitude of the ones you would need to recalculate the waveform lookup table.
That is not an issue at all. I use RAM in the PIC for the waveform table...
So on thought the answer is "kind of but not arbitrarily".
On tests: I get the idea of using a few tomes - but you would end up looking for sone serious test gear to untangle what your speaker produces if you ran a wideband multitone signal through it. (Imagine the mess after all the room reflections and stuff!!!)Posted 26th December 2013 at 01:23 AM by googlyone
-
Thanks for comprehensive answer - however I didn't make my question clear enough it seems as to what I was after. So let me set a little more context first.
An FFT is in effect a bank of narrow bandpass filters, slightly overlapping in centre frequency (due to windowing function smear) but spaced apart to span the whole audio bandwidth. The number of filters is the number of output points (bins) in the FFT - this is usually a power of two and typically 64k.
If the FFT is indeed 64k points then the effective bandwidth of each individual filter (assuming 48k sampling rate) is below 1Hz. Its that figure I was looking for in order to estimate the significance of the noise 'floor' in your plot. The ratio of the individual filter bandwidth to the total audio bandwidth is sometimes called the 'FFT processing gain'.
Yeah I really do want heaps of tones. But they are all low level (they have to be not to overload the system when all added together) - for 300 tones each would be something like -30dBfs. Anyway thanks, I will look at alternative means of generating them!
About the testing - this is only intended for testing electronics, not speakers. Room reflections though wouldn't matter as they don't create new frequencies - this is a test for non-linear distortions.Posted 26th December 2013 at 02:35 AM by abraxalito
-
Richard, any reason you're not doing this sort of thing in something like Audacity?
FrankPosted 28th December 2013 at 10:32 PM by fas42
-
I have done it in Audacity. Just takes a lot of time to assemble all the tones by hand - I was wondering if there was going to be a quicker and more convenient way to play around with different tone spacings and amplitudes than that.Posted 29th December 2013 at 12:51 AM by abraxalito
-
Why not a PC and audacity... There is also something really handy and unencumbered about a standalone piece of kit. No ground noise from the PC, and the ability to fine tune sample rates and implementation.Posted 30th December 2013 at 10:14 PM by googlyone
-
Yep - I'm not a fan of PCs in audio, except in an 'offline' mode. When I've used Audacity, its to prepare a .wav file and transfer that onto an SDcard player.
A standalone signal generator outputting I2S would be very handy, even if it didn't do multione. Would save me storing waveforms from Audacity onto SD. Best if it had the same user interface as my analog sig-gen - i.e. nice big rotating dial.Posted 31st December 2013 at 12:26 AM by abraxalito
-
Hi googlyone,
Are you sharing the source code ?
Quite qurious about generating those signals.
Mainly looking for a nice 2 channel audio function generation with some tricks for different signals.
Like generating 2 channel sine burst signals with controlable switch phases.
Different sweeps, phase inverted etc, on both channels
GenePosted 17th January 2014 at 06:47 AM by gene_klein
-
Yep - no problems at all.Quote:Originally Posted by gene_klein
Hi googlyone,
Are you sharing the source code ?
Quite qurious about generating those signals.
Mainly looking for a nice 2 channel audio function generation with some tricks for different signals.
Like generating 2 channel sine burst signals with controlable switch phases.
Different sweeps, phase inverted etc, on both channels
Gene
I will zip it up and stick it online in the blog section...Posted 25th January 2014 at 02:17 PM by googlyone
