Correct. The web page is still in the archive but the paper can not be downloaded. I posted the paper in one of these threads.
Here it is again.
@john k... could you please show an s-domain / continuous version of your double slope crossover ?
According to your method, if I use a 4th order Butterworth LPF as the base, I would derive an 8th order HPF. However, according to the principles of matched delay subtraction, this derived filter would have the same phase as that of the 4th order filter even though its slope is 8th order....How would you explain that ?
According to your method, if I use a 4th order Butterworth LPF as the base, I would derive an 8th order HPF. However, according to the principles of matched delay subtraction, this derived filter would have the same phase as that of the 4th order filter even though its slope is 8th order....How would you explain that ?
Last edited:
Just to make it clear, if you use a linear phase LP filter with a Butterworth amplitude...
It's by definition: HP= exp(-jwTd) - |LP | * exp(-jwTd), where |#| is the magnitude of the filter response.
Thus, HP = (1 - |LP|) * exp(-jwtTd) = |HP| * exp(-jwTd),
If the |LP| is of the Butterworh family the HP will roll off at twice the order. Conversely, if you do LP = (1- |HP|) exp(-jwt) the LP will roll off at twice the order.
Simple math. No need for more than that. S plane? I don't know. Not my field.
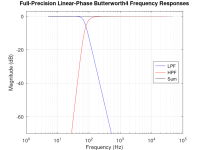
@newvirus2008 , attached are some plots that I'm preparing for my updated MDS Tutorial paper. It works.
Attachments
I understand that part, hence the question.
No problem, I was just trying to see if your method would work with a minimum phase "base" filter, just like Mr. Berchin's method that offers an IIR approximation. Looks like the answer is in the negative ... Please correct me (with proof) if I'm wrong ..
Sir, it definitely works if we:
1) Copy the phase of the delay line to the FIR LPF, or equivalently use a linear phase filter.
I have confirmed this myself in post #400. You seem to have successfully obtained similar results as well.
OR
2) Copy the phase of the minimum phase LPF to the delay line (also confirmed in post# 373.)
However, I (now) think there's no equivalent minimum phase version for this crossover method. There would have been one if it were somehow possible to obtain a matched group delay APF (to the Butter LPF) to take the place of the delay line.
Last edited:
Yes, the result is simply a result of the input having the same phase as the base filter.
HP = (1 - |LP|) * exp(-jwtTd) = |HP| * exp(-jwTd),
Instead of exp(-iwTd) let it be exp(MP(w)) where MP(w) is the minimum phase of the low p[*** Butterworth (or high pass) response, or any arbitrary phase for that matter.
Linear phase was chosen since it results in transient accuracy which was my goal at the time. That was the goal of any of these subtractive filters.
Last edited:
If you use a minimum-phase Butterworth LPF as the "base", then the derived HPF has 3rd-order slope regardless of the order of the LPF.
However, it needs to be possible to have such a filter with the same phase, isn't it ?
The 4th Butterworth is, for example, two biquads at the required cutoff frequency with Q-factors:
What minimum phase APF transfer function would have the exact same phase as this one ?
Last edited:
So many posts in this thread that it's easy to accidentally overlook some of them. You are correct.
That's probably with the true delay... To mimic the JohnK crossover, one needs to match an APF2 phase/delay with that of the LPF4. The closest APF2 I can find is one with Q = sqrt( Q1*Q2 ) where Q1,Q2 are as above and result looks like below. And, even if someone finds out a better filter, there needs to be an explanation for the 8th order slope accompanying a 4th order phase/delay. Thus this method probably is only for the FIR people.
Last edited:
I didn't say (or mean to imply) the all pass was MP. I just mean that it would have to have the same phase as the B4. Easily done with FIR. But, in general all pass filters with frequency dependent, nonlinear phase aren't MP.
Agreed, so what non-linear phase APF transfer function would have the exact same phase as the B4 ?
Sounds very much like it's your field ...
That's the beauty of FIR filters. Take a flat amplitude response, impose the B4 phase, then do an IFft to get the impulse response. But what is the point? You would have the 8th order roll off but the sum, while flat, would not be linear phase, which is the point of the subtractive filters.
Just stuff I picked up along the way.
I'm struggling with exactly what you're asking for here. I think that an example answer might be that you could create a subtractive Linkwitz-Riley crossover with a standard order-2n Butterworth-squared LPF, subtracted from a full-bandwidth signal passed through an order-n allpass filter with the appropriate Q.
Not everyone has "FFT ears" that hear the magnitude and phase separately. My experiments on that topic also indicate something along those lines (until now). I would like to give more attention to arrival time than to phase, especially in a stereophonic environment.
Sir, the point I see in your crossover method is that one could get a steeper rolloff highpass using only a gentler lowpass and some trickery.
I think this method utilises some mathematical "glitch" but since linear phase filters are a necessity for it to exist, the disclosure probably may have had to wait until the same became commonplace.
Now, if it worked with IIR, just imagine the result, an 8th order filter with a 4th order phase and what its transfer function would look like. That would be absolutely magical ...
Last edited:
I would like to give more attention to arrival time than to phase, especially in a stereophonic environment.
virus, please could you open this a little? Arrival time difference in step response (FFT) is another way to tell xo type and frequency, if I understand correctly. Xo type eg. LR2 VS. LR4 rotate phase 180 or 360deg and have difference in arrival time of peaks and polarities
Arrival difference at low freq is longer, is this the reason why low freq phase shift is esier to hear (from single speaker)
Stereophonic listening is very sensitive to polarities, both speakers must have same polarity and same type of xo if they are multiway. As well center speaker of HT should match L/R speakers.
virus, please could you open this a little? Arrival time difference in step response (FFT) is another way to tell xo type and frequency, if I understand correctly. Xo type eg. LR2 VS. LR4 rotate phase 180 or 360deg and have difference in arrival time of peaks and polarities
Arrival difference at low freq is longer, is this the reason why low freq phase shift is esier to hear (from single speaker)
Stereophonic listening is very sensitive to polarities, both speakers must have same polarity and same type of xo if they are multiway. As well center speaker of HT should match L/R speakers.
I don't have anything more to offer.
Phase shift, Phi, is delay,
Phi(w)= w * Td(w). Td(w) = Phi(w)/w.
Any phase other than 0 or linear with frequency results in frequency dependent Td and time distortion.
Phase shift, Phi, is delay,
Phi(w)= w * Td(w). Td(w) = Phi(w)/w.
Any phase other than 0 or linear with frequency results in frequency dependent Td and time distortion.
By arrival times, I mean the arrival times of different speaker channels, hence the mention of a stereophonic environment. Similarly, the arrival times for a multi-way system would have to match, so as to maintain proper time alignment. Like you mentioned, matching is what I believe to be important.
In certain applications like encoding / decoding etc., the linear phase filters are naturally preferred by designers as they're able to more properly reconstruct signals. I think I may be able to hear the effects of phase like interference etc. but, I don't think I can hear "absolute phase" (at least not yet), nor have I personally felt the necessity for linear phase filters.
However, I must admit that my experiments on phase audibility have been 'rudimentary' at best. involving Fourier synthesis of solo instruments etc.
Stereo speaker's different distance in small amount leads to measurable comb filtering which is very difficult to hear binaurally.
Bigger difference shifts center image because of spl difference.
Binaural listening in free space or in a room is very complex and there are numerous studies, including minor unconcious head movement's effect that are needed for localization. Earphone listening is totally different.
Bigger difference shifts center image because of spl difference.
Binaural listening in free space or in a room is very complex and there are numerous studies, including minor unconcious head movement's effect that are needed for localization. Earphone listening is totally different.