John, here is the promised plot
John,
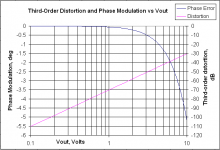
I've taken the equations from Gilbert's paper and extended his example a bit. His example looks at the phase shift at several output levels at a frequency of 1/100 of the gain-bandwidth product. I've changed this a bit. I'm still using 1/100 of the gain-bandwidth product as the test frequency, but I'm plotting the actual phase shift minus the phase shift assuming a linear system. I've called this the phase modulation. I've taken output levels from 0.1 Volt to 10 Volts in 0.1 Volt steps. On the right axis I've plotted the ratio of the third harmonic to the fundamental in dB referenced to the input. Recall that he assumes a distortionless output and computes the distorted input. So I compute the input distortion. I've plotted it against a log voltage scale to show that the distortion is proportional to the amplitude squared per the usual result. This shows that for 1 degree of phase modulation, the third harmonic is not quite 45 dB below the fundamental.
I can provide more info on request, including MathCad and Excel worksheets.
Enjoy.
John,
I've taken the equations from Gilbert's paper and extended his example a bit. His example looks at the phase shift at several output levels at a frequency of 1/100 of the gain-bandwidth product. I've changed this a bit. I'm still using 1/100 of the gain-bandwidth product as the test frequency, but I'm plotting the actual phase shift minus the phase shift assuming a linear system. I've called this the phase modulation. I've taken output levels from 0.1 Volt to 10 Volts in 0.1 Volt steps. On the right axis I've plotted the ratio of the third harmonic to the fundamental in dB referenced to the input. Recall that he assumes a distortionless output and computes the distorted input. So I compute the input distortion. I've plotted it against a log voltage scale to show that the distortion is proportional to the amplitude squared per the usual result. This shows that for 1 degree of phase modulation, the third harmonic is not quite 45 dB below the fundamental.
I can provide more info on request, including MathCad and Excel worksheets.
Enjoy.
Attachments
Mike Gergen said:
I am curious: Is everyone satisfied that:
1)..that NFB is an inherently bad thing?
2)...that 2-tone stimuli provide insight into circuit behaviour that THD analysis cannot?
3)...and that moreover, THD will not detect changes in linearity (or non-linearity thereof) that may be detected by the multi-tone
approach?
Re: Hi Andy...
Well, if I understood John's previous post correctly, his concern was that the mechanism described by Gilbert that causes a variable phase shift of the fundamental with input level, would somehow "hide" from a conventional harmonic distortion test. The graph shows, using Gilbert's equations, that for 1 degree of phase variation from the linear case, the third harmonic is ~45 dB down from the fundamental. So it isn't hiding at all.
BTW, I forgot to mention in my previous post that the plot was taken with a closed-loop gain of 10, same as Gilbert's example.
mikeks said:...what conclusions have you drawn from these results...?
Well, if I understood John's previous post correctly, his concern was that the mechanism described by Gilbert that causes a variable phase shift of the fundamental with input level, would somehow "hide" from a conventional harmonic distortion test. The graph shows, using Gilbert's equations, that for 1 degree of phase variation from the linear case, the third harmonic is ~45 dB down from the fundamental. So it isn't hiding at all.
BTW, I forgot to mention in my previous post that the plot was taken with a closed-loop gain of 10, same as Gilbert's example.
Just to clarify, I'm not in the "harmonic distortion describes everything you need to know about distortion" camp, unless the nonlinearity being considered is memroyless.
Consider the Gilbert article again, where the input stage distorts, but the rest of the amp is distortionless. We know that the same mechanism that produces a third harmonic will also produce a 2f1 - f2 term in a simple two-tone test. Now suppose f2 = 20kHz and f1 = 10010 Hz. We get 2f1 - f2 = 20 Hz. There will be a distortion component at 20 Hz in the diff amp collector current. Don't you agree that the transimpedance ratio (from the freq comp) of 20 kHz vs 20 Hz will tend to make this sideband look much larger at the output relative to the carrier than it is in the collector current waveform? See the problem?
Consider the Gilbert article again, where the input stage distorts, but the rest of the amp is distortionless. We know that the same mechanism that produces a third harmonic will also produce a 2f1 - f2 term in a simple two-tone test. Now suppose f2 = 20kHz and f1 = 10010 Hz. We get 2f1 - f2 = 20 Hz. There will be a distortion component at 20 Hz in the diff amp collector current. Don't you agree that the transimpedance ratio (from the freq comp) of 20 kHz vs 20 Hz will tend to make this sideband look much larger at the output relative to the carrier than it is in the collector current waveform? See the problem?
andy_c said:
Absolutely....but what relative levels are we looking at here...?
Moreover, this is why single pole compensation is not a good idea, (unless it includes the output stage.....but that's another story.)...
Double-pole...or other similarly derived compesation should take care of this....
I am now working on applying Gilbert to a double-pole comp. model......
mikeks said:
If we're talking an IC op-amp with very large open-loop gain, and an open-loop pole less than 20 Hz, (extreme I know), there will be 60 dB difference in open-loop gain between 20 Hz and 20 kHz. Pretty darn big.
Yes, the two-pole compensation is looking better all the time, isn't it? But for IC op-amps, you're stuck with single-pole.
andy_c said:
Which is why externaly compensated op amps are a 'good thing'...
See:
http://www.st-and.demon.co.uk/Audio/700/700page5.html
No a THD meter will not measure this simply because it is a LINEAR "distortion" and not a non-linear.
First, any decent amp will have negligible phase shift in the audio band. Not that it matters because the crossover will induce 45-180 degrees of phase shift anyway. And the human ear is very insensitive to phase shifts. Otherwise everyday living would be pretty hard...
- Status
- This old topic is closed. If you want to reopen this topic, contact a moderator using the "Report Post" button.