What is the Universe expanding into..

[system7]

All these big rides make me feel sick...

The worst one was the Roller-Coaster. The girls were giggling when I was volunteered to take 4-y-o Jessie round it. Apparently I had a grimace on my face the whole experience. Thing is, I had to hold myself and the child in the car when it tried to throw us into the sea on the top corner! 😱

I don't think it was cambered on corners in those days.

Skyways Roller Coaster Clarence Pier POV feat Mr Bean! - YouTube

The rotating teacups were Jessie's favourite. Very calming. Child friendly. We liked the Ghost Train too. Horrible cobwebs in your face in the dark.

Made up for the hideous loud music, flashing lights and the smell of fish and chips and weak vinegar.

 

[Galu]

Help me Bonsai, I've been lured over to the dark side! 😱

 

[Galu]

Now, what were we talking about here?

Ah yes, The Wild Duck Cluster! 😉

Catalogued as M11, it is located in the constellation Scutum (yes, I did spell that correctly!).

It's an open cluster in our galaxy that consists of around 2,900 stars.

Messier 11 (M11) - The Wild Duck Cluster - Universe Today

 

[MITsound]

I can't answer that question, mainly because I can't grasp the concept of an "outside the universe observer".

If you define the universe to mean all the things that could possibly exist in all of space and time, then there can't be anything outside the universe.

There is an outside to our observable patch of the universe, but beyond that boundary there are presumably more galaxies behaving just like the ones we are able to observe.

Sorry. The concept is a simple hypothetical one. I don't even care if the outside observer inhabits more than the usual number of dimensions.

 

[system7]

That's not a Duck, Galu. It's got to walk like a Duck, and quack like a Duck to probably be a Duck! 😀

I am not uncomfortable with us living in an expanding observed Universe of radius 46 Bn light years within a time scale of 13.8 Bn years.

You must always be clear if you are an intrinsic observer living on its surface, or getting in a muddle and thinking (wrongly) that you can observe it from the outside (extrinsic observer).

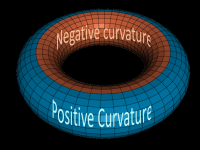
This is a fanciful visualisation of what our Universe might look like from the outside if it is a doughnut or torus:

Can we determine the Extrinsic Geometry by anything we measure on the inside?

Cue the Prince of Mathematicians Carl Friedrich Gauss who thought about this:

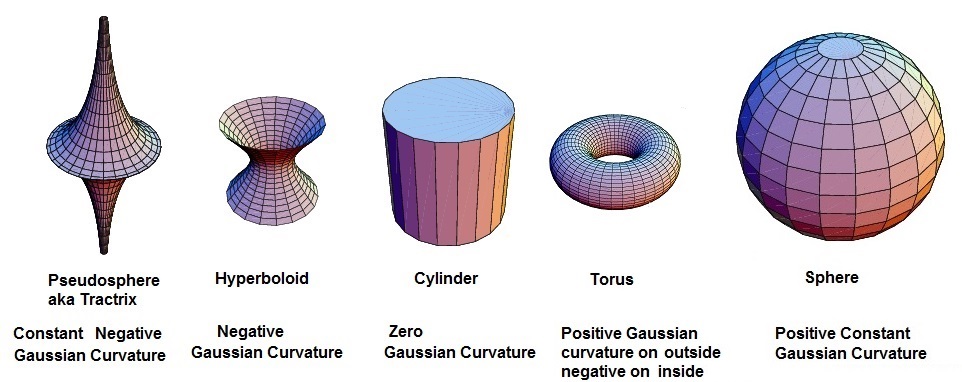
(This is 2d embedded in 3D. We then must stretch our mathematical minds to think about 3D embedded in 4D...)

Maybe. We might be able to determine the curvature, positive, negative or flat with big measurements. On the small scale everything looks the same to the ants crawling over any of these 2D surfaces.

Interestingly, in 4D, the curvature rules are different, and a Torus is Flat.

 

[Bonsai]

“Interestingly, in 4D, the curvature rules are different, and a Torus is Flat.”

Can you explain this statement or show a visualization?

 

[Galu]

You must always be clear if you are an intrinsic observer living on its surface, or getting in a muddle and thinking (wrongly) that you can observe it from the outside (extrinsic observer).

Spacetime curvature can be described in either intrinsic or extrinsic terms.

Because it is difficult to visualise a four dimensionsal spacetime, the torus is often used to illustrate the difference between the two terms.

The curvature we see in a doughnut shaped torus is extrinsic. The inside has negative curvature while the outside has positive curvature.

However it can be represented with zero intrinsic curvature on the flat screen of a Pacman video game where Pacman leaves the top and emerges at the bottom, or exits the right and enters the left and visa versa.

Steve, the mathematician, can probably explain it better. Apparently the curvature of a torus that we see as a doughnut is extrinsic due to its embedding in three dimensions.

 

[system7]

I have discovered a Duck Cluster closer to home! 😎

And it looks much more like Ducks than Galu's Messier 11 example! 😀

Between No. 19 and No. 23 Eldon Street, Portsmouth, lies a yellow dwelling with no number on its front door, but which does have a letter box, though I expect the parcel courier leaves stuff next door. But it has 21 Ducks in the window. I suppose this is to help the Fire Brigade find it after a 999 call... 😕

Research into Doughnuts is currently ongoing.

Post-Doc Ergo Propter Hoc: The Simpson-Hawking Donut Universe

I hope to have more to say when the smoke clears.

 

[Galu]

Looks like the sort of dwelling where a quack would live! 😉

 

[Bonsai]

What kind of smoke would that be Steve?

 

[Galu]

A cosmic smoke ring?

 

[system7]

All donuts, Galu!

Here's something about colliding donuts (Tori) I find interesting.

When you collide them, they splatter into 24 pieces! 😎

24 being John Baez's favourite number:

My Favorite Numbers

Bonsai asked me to help him visualise a 3D donut embedded in 4Dspace. It's hard. But a flat Hyperdonut seems to exist:

This metric of the square flat torus can also be realised by specific embeddings of the familiar 2-torus into Euclidean 4-space or higher dimensions. Its surface has zero Gaussian curvature everywhere. Its surface is flat in the same sense that the surface of a cylinder is flat. In 3 dimensions, one can bend a flat sheet of paper into a cylinder without stretching the paper, but this cylinder cannot be bent into a torus without stretching the paper (unless some regularity and differentiability conditions are given up, see below).

Torus - Wikipedia

Gaussian Curvature is Intrinsic to a surface (or volume, I believe):

Gauss's Theorema egregium (Latin: "remarkable theorem") states that Gaussian curvature of a surface can be determined from the measurements of length on the surface itself. In fact, it can be found given the full knowledge of the first fundamental form and expressed via the first fundamental form and its partial derivatives of first and second order.

Equivalently, the determinant of the second fundamental form of a surface in R3 can be so expressed. The "remarkable", and surprising, feature of this theorem is that although the definition of the Gaussian curvature of a surface S in R3 certainly depends on the way in which the surface is located in space, the end result, the Gaussian curvature itself, is determined by the intrinsic metric of the surface without any further reference to the ambient space: it is an intrinsic invariant.

In particular, the Gaussian curvature is invariant under isometric deformations of the surface.

Gaussian curvature - Wikipedia

In our 3D space, flatness is lost without some mighty fractal trickery:

The Tortuous Geometry of the Flat Torus | Science4All

Discovered by Russell Crowe in his John Nash film, "A Beautiful Mind". We've all seen it, right? Along with Anthony Hopkins in "Proof", another Maths movie. 🙂

 

[MITsound]

I can't answer that question, mainly because I can't grasp the concept of an "outside the universe observer".

If you define the universe to mean all the things that could possibly exist in all of space and time, then there can't be anything outside the universe.

There is an outside to our observable patch of the universe, but beyond that boundary there are presumably more galaxies behaving just like the ones we are able to observe.

Is there not a theory that ours is not the universes but one of many universes, which are a grouping of micro foamy "bubbles"?
Perhaps relative to their individual bubbles, any observer within one would find whatever distance is, too vast to see another universe, if it even has photons.
Or if photons can traverse something between that is truly nothing.

 

[TNT]

A duck or "not a duck"?

That is the cosmic question! 😉

:-D

//

 

[Galu]

All donuts, Galu!

Have you gone all 'American' on us, Steve?

Give me a big sugary doughnut any time!

P.S. There appears to be a spelling mistake at the top of your John Baez link.

It should read The Rankine Lecture and not The Rankin Lectures, so I'm not surprised the link does not work.

The Rankine Lecture is named after William Rankine FRSE FRS who was a Scottish mechanical engineer and founding contributor to the science of thermodynamics.

Rankine scale - Wikipedia

P.P.S. I hope Bonsai is satisfied with the explanation that a torus which is embedded into four dimensions has a flat curvature - I knew that all along! 😉

 

[Galu]

Steve, your other link shows a good stab at how a flat sheet of zero curvature can be transformed into a torus - so I'll attach the illustration here.

Note that some allowable stretching is required!

The link given to the YouTube video on 'gluing a torus' is also worth reproducing here:

Gluing a Torus - YouTube

 

[Galu]

Is there not a theory that ours is not the universes but one of many universes, which are a grouping of micro foamy "bubbles"?
Perhaps relative to their individual bubbles, any observer within one would find whatever distance is, too vast to see another universe, if it even has photons.
Or if photons can traverse something between that is truly nothing.

Yes, I'm familiar with the 'Bubble Universe' hypothesis.

The idea is that our universe is a swelling bubble, outside of which more bubble universes exist.

I remember discussing the possibility of bubble universe collision earlier in the thread.

However, and perhaps pertinent to your post, communication between bubble universes may not be possible.

I recall that the different universes may have different physical constants - such as the speed of light in a vacuum - and therefore have different laws of physics.

 

[Bonsai]

Excellent videos! So a Torus is indeed a flat sheet of paper with just two cuts (Science4All video).

 

[system7]

If I remember right, the famous Klein Bottle is a rolled up flat sheet too:

But you twist one end the other way (in 4D, of course) to create something that isn't a doughnut. A sort of mobius thing, er, I think. Thing is, you can do all sorts of unexpected things with a square flat sheet by changing the direction of the arrows around. The computer game "Portal" exploits this idea with Red and Blue portals that do unexpected things.

Klein Bottles aren't orientable, unlike the torus:

Orientability - Wikipedia

Though a certain Mobiusness lurks even in the Torus in 3D, as the mad bagel-loving professor here explains:

Topology of a Twisted Torus - Numberphile - YouTube

He says the carefully cut Bagel is a "Cosmic Concentrator" that can harness the power of Black Holes! 😎

Just to see if you are paying attention, what would a topologist see in the extremely interesting Costa Minimal Surface pictured below? It's an exotic soap bubble in essence.

(Ans: A thrice punctured Torus of course. 🙂 )

I have wondered if I could get a Costa Surface to fly if I put propellors in the holes. 😕

 

[Galu]

If I remember right, the famous Klein Bottle is a rolled up flat sheet too...
But you twist one end the other way (in 4D, of course) to create something that isn't a doughnut. A sort of mobius thing, er, I think.

If you cut a Klein bottle in half along its length you get two Mobius strips.

Okay, how do you cut a Kein bottle in half?

First thing you need is a diamond saw!

Cutting a Klein Bottle in Half - Numberphile - YouTube

I've never seen anyone get so excited by topology! 😀