I started this post yesterday. It describes a PLLXO between two 2SK170 buffers. I'm also using this circuit for buffering a volume pot. I think it's the most simple low distortion voltage follower one can build. The 2SK170 are obsolete and hard to get, bur you can easily substitute them with J133 or LSK170.
Its obvious you've done a lot of design and work on this... normal opamps have got to be the way forward for something like this. Although purists may not agree I would consider simply attenuating the input to get the headroom you need. If you are looking at signals that come close to -/+24 volts then a microscopic noise penalty has to be way down the list. I wouldn't even consider thinking of bootstrapping stages to get more headroom.
I studied the Bainter Notch and found someone else's working circuit here: https://electroagenda.com/en/bainter-notch-filter-design-and-tuning/
It looks like the headroom problem with the original and derived circuits at the A output can be mitigated by decreasing K1 (or increase HF path gain in some way, like some high-Z input buffer -- with gain or attenuation -- missing in below schematic).
To get the same LF to HF ratio in the R4-R5-C2 mixer, the ratio of R4/R5 must be reduced, and that reduces the A output wrt final output for DC and LF.
HF corner frequency stays the same when R4//R5 parallel value is maintained. Overall gain also remains set by the HF path with K2 (which we' prefer to have unity, a simple buffer)
To have the DC/LF feedback at the same level as seen by A K2 could be increased reciprocal to the K1 change, or R3 be altered (or even replaced by a divider).
Corner frequency might shift unless R1 and C1 are adjusted as well.
----:----
All in all I would think this is a prime example where a simulation would shed some light on things and then ways can be found to have a more even distribution of gains at the various cells that maximizes headroom with little, if any degradation in other parameters. It will likely have overall gain ~2x...3x but no stage will be suffering from lack of headroom early on vs the others.
It looks like the headroom problem with the original and derived circuits at the A output can be mitigated by decreasing K1 (or increase HF path gain in some way, like some high-Z input buffer -- with gain or attenuation -- missing in below schematic).
To get the same LF to HF ratio in the R4-R5-C2 mixer, the ratio of R4/R5 must be reduced, and that reduces the A output wrt final output for DC and LF.
HF corner frequency stays the same when R4//R5 parallel value is maintained. Overall gain also remains set by the HF path with K2 (which we' prefer to have unity, a simple buffer)
To have the DC/LF feedback at the same level as seen by A K2 could be increased reciprocal to the K1 change, or R3 be altered (or even replaced by a divider).
Corner frequency might shift unless R1 and C1 are adjusted as well.
----:----
All in all I would think this is a prime example where a simulation would shed some light on things and then ways can be found to have a more even distribution of gains at the various cells that maximizes headroom with little, if any degradation in other parameters. It will likely have overall gain ~2x...3x but no stage will be suffering from lack of headroom early on vs the others.
There is: everything possible exists in our universe:
https://www.radiomuseum.org/tubes/tube_tca220.html
Thanks for your thoughts but many of your suggestions are unfortunately not going to work. A SPICE sim is not all that useful - I need to compute all the component values. I entered all of the design equations into a spreadsheet and the transfer function is given directly in the 1975 Bainter paper. You cannot play games with K1 and K2 arbitrarily. For example K2 IS the HF gain and it is not influenced by any component values or K1 or A. You can see this from EQ8 (the transfer function) in the link you posted.
For a lowpass notch you want the passband to be unity gain. The passband is the response in the LF limit W<<Wp. But this means that in the HF limit the gain must be lower by the factor (Wp/Wz)^2, where Wz can be up to about 5 *Wp or even 6*Wp. This means that the overall passband GAIN for the lowpass notch can be 24dB or more (up to 40dB in some extreme cases).
Note that in the link the author only works with the symmetric notch. Wayyyyyy easier than the lowpass notch form!
Anyway, the Bainter circuit is nice in that it has orthogonal adjustability on Wp, Wz and Q. Also exact cap values are not needed because the circuit can be designed with the actual capacitances (which are unfortunately your random luck of the draw from the distribution of values) and only a couple of resistances need to be tweaked to restore the target parameter values.
There is another useful circuit for the lowpass and highpass notch - Friend's biquad. It is a marvel of a single op-amp circuit. But the gain in the passband cannot be strictly controlled and depends on the notch parameters, so I thought that the Bainter cirucit would be better for DIY.
Last edited:
IMHO a SPICE sim is always very useful to gain insight on a circuit's inner workings, much more than the purely analytical derivation of component values, at least for me. And most often I've found ways to modify a circuit to fulfill some design constraints or deal with side effects not covered in the original literature or whatever source we're building upon.
Then again, I have not yet built or simmed a Bainter Notch so I'm not really qualified to make an explicit statement here.
I do, though, use notch filters for distortion measurements and I'm quite happy with the performance of simple passive Hall network notches which also can be made high Q with some feedback from the output buffer.
Well I think I have found a fatal flaw now in the Bainter notch, at least for my needs. As I mentioned above, K2 alone sets the HF output level. The Lowpass notch has a passband for frequencies below Wp and we generally want the passband gain to be equal to 1. The lowpass notch requires that K2 take on the value of (Wp/Wz)^2 and the ratio Wp/Wz can be up to about 5 or possibly even 6. So K2 might be as low as 1/36th which equals 0.025, which is about -31dB.
Look at the Bainter circuit, just above in post #23. The last op amp sets K2, which we know must have a gain of -31dB gain. But since the passband of the lowpass notch should have unity gain, the only way for that to happen with K2 having a gain of -31dB is if the voltage coming out of amplifier A is above this value. That is for 1 Volt output coming out of the circuit from K2 the input to K2 must be up to (in our example case) 36 *(R4+R5)/R5 HIGHER in voltage! When the circuit is designed for Wp/Wz=6, both R4 and R5 are about the same value (e.g. 6k Ohm) so (R4+R5)/R5 is another factor of 2. That means the voltage coming out of A must be 72 times the output voltage. Even if using bootstrapping or ultra-high rail voltage op-amplfiers for A this does not seem practical (unless someone has a bright idea about that). I didn't even need a SPICE sim to figure this out...
Keep in mind that this problem occurs for the lowpass notch only, but that form is critical for my needs. As a result, this circuit seems like a total fail for much of the lowpass notch parameter space that I would need to use it in.
Time to move on to Friend's biquad...
Look at the Bainter circuit, just above in post #23. The last op amp sets K2, which we know must have a gain of -31dB gain. But since the passband of the lowpass notch should have unity gain, the only way for that to happen with K2 having a gain of -31dB is if the voltage coming out of amplifier A is above this value. That is for 1 Volt output coming out of the circuit from K2 the input to K2 must be up to (in our example case) 36 *(R4+R5)/R5 HIGHER in voltage! When the circuit is designed for Wp/Wz=6, both R4 and R5 are about the same value (e.g. 6k Ohm) so (R4+R5)/R5 is another factor of 2. That means the voltage coming out of A must be 72 times the output voltage. Even if using bootstrapping or ultra-high rail voltage op-amplfiers for A this does not seem practical (unless someone has a bright idea about that). I didn't even need a SPICE sim to figure this out...
Keep in mind that this problem occurs for the lowpass notch only, but that form is critical for my needs. As a result, this circuit seems like a total fail for much of the lowpass notch parameter space that I would need to use it in.
Time to move on to Friend's biquad...
I can see your point and it triggered me to do some simulations to mitigate those problems of the standard lowpass-derived Bainter Notch filter.
One thing is that Q factors (without the degeneration resistor) of seven or higher did not lead to any really practical circuits I could come up with. The lowpass section has the same Q by definition which gives accordingly heavy peaking (of 20dB and more) and that alone can quickly eat up any reasonable headroom.
However, for Q factors of 5 and lower I think I found a solution for following, somewhat arbitrary conditions (yours might well be different):
- 1kHz, Qmax=7 (so practical Q after trimming can safely reach a value of 6).
- Input voltage 2Vrms, purely resistive loading preferred (the original circuit has some frequency-dependent input impedance).
- +-15 or +-18V rails which sets available headroom. Circuit shall not clip even with complex wideband signals but shall offer good S/N ratio.
- Unity Gain (but Gain = -1 is OK also).
- Controlled Notch Depth of -40dB.
- OpAmp input node impedances preferably 2kOhm'ish for low noise with bipolar OpAmps but still OK to drive.
Key idea is to reduce the input gains for highpass and lowpass path by the same factor so the lowpass output at the peak frequency does not clip. After the mixer I use simple non-inverting makeup gain to get the required overall gain of unity or other values (note that it does not impact anything else, the feedback gain is always 1 here).
Of course, it's all about trade-offs and here the main disadvantage is that noise and distortion behavior degrades quickly with larger Q values but the main virtues of the Bainter notch, notch Q and notch depth stability and generally a low component value sensitivity are retained.
@KSTR
Thanks for taking the time to look into this circuit and explore the problem and possibilities! I appreciate it.
Since you are exploring the parameter space in which your circuit will work, let me give you some examples where I found that the original Bainter circuit would not work. This is confined to the lowpass notch form from what I can tell. These sorts of filter repsonses are building blocks for elliptic filters, and I have been working on filters with similar responses but that are optimized for loudspeaker crossover. So for example, these parameters would be required:
lowpass notch
Fpole =1000
Qpole =2.95
Fzero =1700
or how about a more challenging example:
Fpole =585
Qpole =0.6
Fzero =7200
These should both produce unity gain for F<<Fpole. The second one has, for F>>Fpole gain=-43dB or so, which is an example of what is not practical using the Bainter circuit.
For my needs Q values are never as high as 9, maybe 5 max and rarely that high.
Can you try your circuit with the second notch parameters?
Thanks for taking the time to look into this circuit and explore the problem and possibilities! I appreciate it.
Since you are exploring the parameter space in which your circuit will work, let me give you some examples where I found that the original Bainter circuit would not work. This is confined to the lowpass notch form from what I can tell. These sorts of filter repsonses are building blocks for elliptic filters, and I have been working on filters with similar responses but that are optimized for loudspeaker crossover. So for example, these parameters would be required:
lowpass notch
Fpole =1000
Qpole =2.95
Fzero =1700
or how about a more challenging example:
Fpole =585
Qpole =0.6
Fzero =7200
These should both produce unity gain for F<<Fpole. The second one has, for F>>Fpole gain=-43dB or so, which is an example of what is not practical using the Bainter circuit.
For my needs Q values are never as high as 9, maybe 5 max and rarely that high.
Can you try your circuit with the second notch parameters?
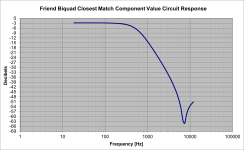
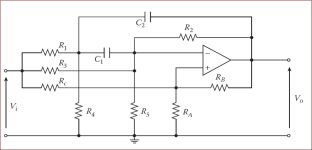
Another circuit that can create the lowpass notch response is Friend's biquad. The circuit diagram is attached. The values in the table should result in the response following the second notch shown above, as shown in the attached plot. It is tricky to get the gain any higher in the passband. This is about as high as I could get it before things fall apart. The circuit requires only a single op-amp but the load on its output is sometimes a bit low and adding a trailing buffer/voltage follower is probably a good idea. With some careful component selection this circuit works pretty well and often the passband gain can be brought up to 0dB or near that, and that would be OK. There would only be 3 or 4 of these in series at most, so a few dB here and there can be made up in the final buffer.
I'm not sure if anything bad is going on within the circuit, at all the nodes, since I have not done a SPICE sim.
I'm not sure if anything bad is going on within the circuit, at all the nodes, since I have not done a SPICE sim.
| Closest Match to Available Component Values: | ||
| value | component | series |
1.000E-08 | C1 [Farad] | |
1.000E-08 | C2 [Farad] | |
2,740 | RA [Ohm] | E192 |
27,100 | RB [Ohm] | E192 |
634,000 | RC [Ohm] | E192 |
25,800 | R1 [Ohm] | E192 |
412,000 | R4 [Ohm] | E192 |
2,080 | R2 [Ohm] | E192 |
| omit | R3 [Ohm] | E192 |
223 | R5 [Ohm] | E192 |
2843.05 | component spread = max R / min R |
Attachments
Last edited:
Ah OK, now I understand. With these parameters we basically have a low pass with some required Q and way up we have an overlayed notch.
Looks like this can be synthesized with the proposed circuit very well:
Prescaling gain is 0.5x but the Q reduction bumps the lowpass output back up to -1dB, for a decent headroom.
The low Q of the pole avoids peaking and noise gain here very well. Same goes for the required additional headroom for complex wideband signals which will be very small here.
The notch higher up is then created by mixing in just a little bit of the input signal rather than referring the second lowpass capacitor C_hp to GND (as seen from the lowpass POV).
Again we have a drawback, there is no control of notch Q and it becomes very low once the notch frequency moves away from the pole frequency. There is basically no more feedback available down this low in the lowpass slope to increase notch Q.
Then again, when you don't need the adjustability of the Bainter type of filters and when the performance of the Friend Biquad is stable and not any worse than the Bainter in various regards, I'd go for the latter. Noise gain in circuits with positive feedback always needs to monitored to avoid unpleasant surprises. ;-)
Personally, I'd probably also take a look at separate and cascaded lowpass and notch filter blocks to have full control over lowpass Q and slope (and zeros, if any) as well as over the notch Q and depth, besides their individual frequencies: https://sound-au.com/articles/ntm-xover.htm
@KSTR As you suggest (and do) separating the lowpass function and notch-forming reverse phase highpass, and then summing these appropriately, is probably the best way to create this response when Fzero>>Fnotch. When the notch is so far down the LP function the exact Q value is probably not critical.
Coming back to this, I see two issues with the Friend biquad here:
- the circuit is brutally sensitive to component tolerances and drifts
- the noise gain, as expected, is going straight through the roof to over 40dB at DC/LF, and still 25dB at 10kHz. Hardly nice conditions for the OpAmp wrt noise and distortion :-(
@CharlieLaub,
"better" depends on what the goals are, doesn't it?
The (modified) Bainter would be my choice for an universal dependable laboratory notch with fine-trims for everything. The Bainter was new to me and I'm impressed by the stability (in sim world, for now).
As for Biquads of any color, I think it comes down to the same that we see with the Bainter. Once you have a known and preferably well restricted parameter set you can start and play with circuit optimization and small rearrangements to arrive at a well-working circuit with known and controlled trade-offs. However, some more extreme solutions, like the Friend Biquad, may never behave as nice as a Bainter wrt components sensitivity. And with those double integrator Biquads I've seen headroom issues as well when designed strictly as per equations.
For loudspeaker crossover duty, many time I've used Sallen-Key filters with "inside" secondary filter elements to modify the response at points sufficiently far away from the filter frequency. With a bit of luck and extensive CAE optimizer support that can lead to very compact circuits with very few OpAmp stages and still moderate component sensitivity. I tend to avoid any Q's above 2 anyway ;-)
"better" depends on what the goals are, doesn't it?
The (modified) Bainter would be my choice for an universal dependable laboratory notch with fine-trims for everything. The Bainter was new to me and I'm impressed by the stability (in sim world, for now).
As for Biquads of any color, I think it comes down to the same that we see with the Bainter. Once you have a known and preferably well restricted parameter set you can start and play with circuit optimization and small rearrangements to arrive at a well-working circuit with known and controlled trade-offs. However, some more extreme solutions, like the Friend Biquad, may never behave as nice as a Bainter wrt components sensitivity. And with those double integrator Biquads I've seen headroom issues as well when designed strictly as per equations.
For loudspeaker crossover duty, many time I've used Sallen-Key filters with "inside" secondary filter elements to modify the response at points sufficiently far away from the filter frequency. With a bit of luck and extensive CAE optimizer support that can lead to very compact circuits with very few OpAmp stages and still moderate component sensitivity. I tend to avoid any Q's above 2 anyway ;-)
Thanks for your thoughts. I was hoping to arrive at a particular circuit that does not need optimization of the circuit itself, only adjust of e.g. resistor and capacitor values to obtain the desired response withing some reasonable parameter space. I guess I am too removed from these realities after only working with IIR DSP for the past 10+ years...
I woke up early today and after some coffee I looked up some biquad circuits on the web. While doing that I came across this page:
https://mysite.du.edu/~etuttle/electron/elect65.htm
In the section "Notch Filter" near the end (see image below) the author explains how the LP and HP outputs of the three-op-amp biquad can be summed to form the notch filter. What I found interesting and that I did not quite grasp previously was that you can use an inverting summer to weight each output. I sort of knew this in general before, but what the author explains next made a lightbulb turn on in my head:
In the text shown in the image, the author gives an example how a lowpass notch could be formed. Because of the weighting of BOTH responses in the summer, the HP notch can be formed that way as well. Also, the weighting of both allows the designer/builder to set the passband gain to unity (or whatever is desired). I believe these three-op-amp biquad type circuits are low sensitivity. Not sure about the noise gain, however.
Although it requires four op-amps this seems like a circuit that a DIYer could design and build and that would work the same no matter what notch parameters are needed. This type of biquad circuit usually allows orthogonal tuning of F and Q.
https://mysite.du.edu/~etuttle/electron/elect65.htm
In the section "Notch Filter" near the end (see image below) the author explains how the LP and HP outputs of the three-op-amp biquad can be summed to form the notch filter. What I found interesting and that I did not quite grasp previously was that you can use an inverting summer to weight each output. I sort of knew this in general before, but what the author explains next made a lightbulb turn on in my head:
In the text shown in the image, the author gives an example how a lowpass notch could be formed. Because of the weighting of BOTH responses in the summer, the HP notch can be formed that way as well. Also, the weighting of both allows the designer/builder to set the passband gain to unity (or whatever is desired). I believe these three-op-amp biquad type circuits are low sensitivity. Not sure about the noise gain, however.
Although it requires four op-amps this seems like a circuit that a DIYer could design and build and that would work the same no matter what notch parameters are needed. This type of biquad circuit usually allows orthogonal tuning of F and Q.
Attachments
Last edited:
I agree, a great resource, thanks for sharing.
When cascading stages one could even split up the Rg of a subsequent stage into a resistive mixer with the proper ratio and same output impedance and save an OpAmp. I like it when things fall neatly in place like this ;-)
Just found this paper, which is using the circuit shown above and also discusses passive ladder realizations, which I am very interested in. I wish I had found this a couple of weeks ago!
https://www.researchgate.net/publication/221375860_Tuning_Elliptic_Filters_with_a_'Tuning_Biquad'
https://www.researchgate.net/publication/221375860_Tuning_Elliptic_Filters_with_a_'Tuning_Biquad'