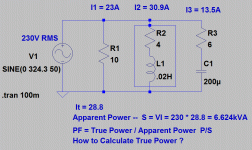
I have attached a picture of a parallel RLC circuit that I am trying to calculate the Power Factor.
Branch 1 is a Resistor of 10 Ohms
Branch 2 is an Inductor of .02H & has 4 Ohms DC resistance.
Branch 3 is a 6 0hm Resistor with a 200uF Capacitor in Series.
I have calculated the Branch Impedances, Inductive Reactance, Capacitive Reactance, Currents etc & also the Apparent Power kVA.
I am trying to work out how to get the Power Factor of this circuit.
PF = True Power/ Apparent Power P/S =?
I am not sure how to Find the True Power?
I have looked at different formula's but none of them seem to work for my pea sized brain, can someone help me out with this, I thought that the equation for Apparent power was for True power but obviously not?.
Cheers.
Branch 1 is a Resistor of 10 Ohms
Branch 2 is an Inductor of .02H & has 4 Ohms DC resistance.
Branch 3 is a 6 0hm Resistor with a 200uF Capacitor in Series.
I have calculated the Branch Impedances, Inductive Reactance, Capacitive Reactance, Currents etc & also the Apparent Power kVA.
I am trying to work out how to get the Power Factor of this circuit.
PF = True Power/ Apparent Power P/S =?
I am not sure how to Find the True Power?
I have looked at different formula's but none of them seem to work for my pea sized brain, can someone help me out with this, I thought that the equation for Apparent power was for True power but obviously not?.
Cheers.
Attachments
Last edited:
true power is actual consumed power. In your circuit only resistances are dissipating (consuming) power. So, calculate power dissipation by R1, R2, R3, sum them up and you get a true power (calculate currents through resistors and use formula I^2*R)
Apparent Power = total current through circuit * applied Voltage (do not forget you have reactive elements in the circuit)
PF=True Power/apparent power
Apparent Power = total current through circuit * applied Voltage (do not forget you have reactive elements in the circuit)
PF=True Power/apparent power
I would use AC analysis (not transient) as its a linear network. This then will give you the current from the source and its phase. Then true power is calculated by taking the cosine of the phase angle (the PF) and multiplying this by the apparent power. I think, I haven't tried it....
Thanks for the replies,
Irakli,
I am a little confused with this.
So I just use the Resistance values of R1, R2, R3 & not the Z Impedance total value of each branch?
I calculated things using the Parallel resistance calculation & then the current for each branch but things don't seem correct.
So do I just Add R1 + R2 + R3 which gives 20 Ohms?
230V/20R = 11.5A
True Power = I^2 * R = 132.25 * 20 = 2.645kW
PF = P/S True Power/ Apparent Power
= 2.645kW/6.624kVA
PF = .4
Is this correct, I thought I may have to use the Z impedance total for each brach in parallel & then work things out from there?
I have to say I am a little confused.
Cheers
Irakli,
I am a little confused with this.
So I just use the Resistance values of R1, R2, R3 & not the Z Impedance total value of each branch?
I calculated things using the Parallel resistance calculation & then the current for each branch but things don't seem correct.
So do I just Add R1 + R2 + R3 which gives 20 Ohms?
230V/20R = 11.5A
True Power = I^2 * R = 132.25 * 20 = 2.645kW
PF = P/S True Power/ Apparent Power
= 2.645kW/6.624kVA
PF = .4
Is this correct, I thought I may have to use the Z impedance total for each brach in parallel & then work things out from there?
I have to say I am a little confused.
Cheers
Last edited:
Hi Irakli,
I did that before but something doesn't seem right.
R1 = 230/10 =23A
R2 = 230/4 =57.5A
R3 = 230/6 =38.3A
IT = 118A
Where to from here as things don't seem right?
Cheers
I did that before but something doesn't seem right.
R1 = 230/10 =23A
R2 = 230/4 =57.5A
R3 = 230/6 =38.3A
IT = 118A
Where to from here as things don't seem right?
Cheers
OK, let' do it by book, with some compex numbers:
1. Let's calculate total complex impedance of the circuit.
1/Ztot=1/Z1+1/Z2+1/Z3
Z1=R1=10ohm
Z2=R2+j*2*Pi*f*L=4+J*6.28*50*0.02=4+j*6.28 (4 is a real part and 6.28 is imaginary part of the Z2 impedance)
Z3=R3+j/(2*Pi*f*C)=6-j*15.92 (please doublecheck the math yourself).
Thus, current I=V/Z=V*(1/Z)=230*(1/Z)=44.36-j*13.61
As you see current has real and imaginary parts.
Now we need to calculate angle between voltage and current.
tg(a)=Im(I)/Re(I)=-13.61/44.36=-0.31
"a" is an angle how much current is shifted vs. voltage.
Power Factor is simply PF=|cos(a)|. Knowing tg(a) you find |cos(a)|
|cos(a)|=sqrt(1/(1+tg(a)*tg(a)))=0.96 (again, please check math to be sure)
1. Let's calculate total complex impedance of the circuit.
1/Ztot=1/Z1+1/Z2+1/Z3
Z1=R1=10ohm
Z2=R2+j*2*Pi*f*L=4+J*6.28*50*0.02=4+j*6.28 (4 is a real part and 6.28 is imaginary part of the Z2 impedance)
Z3=R3+j/(2*Pi*f*C)=6-j*15.92 (please doublecheck the math yourself).
Thus, current I=V/Z=V*(1/Z)=230*(1/Z)=44.36-j*13.61
As you see current has real and imaginary parts.
Now we need to calculate angle between voltage and current.
tg(a)=Im(I)/Re(I)=-13.61/44.36=-0.31
"a" is an angle how much current is shifted vs. voltage.
Power Factor is simply PF=|cos(a)|. Knowing tg(a) you find |cos(a)|
|cos(a)|=sqrt(1/(1+tg(a)*tg(a)))=0.96 (again, please check math to be sure)
Hi Irakli,
I'm sure your math is correct & thank you very much for that, unfortunately I do not understand complex numbers at this stage as I am only learning😕.
Could you possibly help me with standard math numbers.
Thank You
Cheers
I'm sure your math is correct & thank you very much for that, unfortunately I do not understand complex numbers at this stage as I am only learning😕.
Could you possibly help me with standard math numbers.
Thank You
Cheers
Here is another way to calculate;
1. determine |Z1|, |Z2| and |Z3|
e.g. |Z2|=sqrt (R2*R2+wL*wL) where w=2*Pi*f
2. calculate currents through each branch (your simulator already shows them)
|I1|=23A, |I2|=30.9 , |I3|=13.52
calculate power dissipated by ACTIVE elements (resistors) in each branch
true power (power which is converted into heat) P=P1+P2+P3=R1*I1^2+R2*I2^2+R3*I3^2=5290+3812+1097=10199=10.20KW (thats a lot of power,lol)
Now we need to calculate apparent power which is S=|V|*|Itot|=230*|Itot|
Itot is not simply a sum of |I1|+|I2|+|I3|. I think thats where you have a problem. You need to sum currents as vectors and then find the magnitude.
as I mentioned in previous post, Itot=44.36-j*13.61. So, |itot|=sqrt(44.36^2+13.61^2)=46.06A (not 118A as in your calculations)
Apparent power S=230*46.06=10594W
power Factpr PF=10.20/10.59=0.96
Have fun 🙂
1. determine |Z1|, |Z2| and |Z3|
e.g. |Z2|=sqrt (R2*R2+wL*wL) where w=2*Pi*f
2. calculate currents through each branch (your simulator already shows them)
|I1|=23A, |I2|=30.9 , |I3|=13.52
calculate power dissipated by ACTIVE elements (resistors) in each branch
true power (power which is converted into heat) P=P1+P2+P3=R1*I1^2+R2*I2^2+R3*I3^2=5290+3812+1097=10199=10.20KW (thats a lot of power,lol)
Now we need to calculate apparent power which is S=|V|*|Itot|=230*|Itot|
Itot is not simply a sum of |I1|+|I2|+|I3|. I think thats where you have a problem. You need to sum currents as vectors and then find the magnitude.
as I mentioned in previous post, Itot=44.36-j*13.61. So, |itot|=sqrt(44.36^2+13.61^2)=46.06A (not 118A as in your calculations)
Apparent power S=230*46.06=10594W
power Factpr PF=10.20/10.59=0.96
Have fun 🙂
Thanks Irakli,
I now see where I was going wrong & you were correct where you mentioned it:
"Itot is not simply a sum of |I1|+|I2|+|I3|. I think thats where you have a problem. You need to sum currents as vectors and then find the magnitude.
as I mentioned in previous post, Itot=44.36-j*13.61. So, |itot|=sqrt(44.36^2+13.61^2)=46.06A (not 118A as in your calculations)"
This is where I was stumbling but now I see how you have worked it out.
Thank You very much for your time, greatly appreciated😀!
Cheers
I now see where I was going wrong & you were correct where you mentioned it:
"Itot is not simply a sum of |I1|+|I2|+|I3|. I think thats where you have a problem. You need to sum currents as vectors and then find the magnitude.
as I mentioned in previous post, Itot=44.36-j*13.61. So, |itot|=sqrt(44.36^2+13.61^2)=46.06A (not 118A as in your calculations)"
This is where I was stumbling but now I see how you have worked it out.
Thank You very much for your time, greatly appreciated😀!
Cheers
Last edited:
Hi again Irakli,
In your equations you get IT = 46.06A.
Using the following calculation I seem to get a different number.
(I1= 23A, I2 = 30.9A, I3 = 13.52A)
IT = sqrt I1^2 + (I2 - I3)^2
= sqrt 23^2 + 30.9-13.52^2
= sqrt 529 + 302
= sqrt 831
= 28.8A
Could you have a look & see what you think, I think this may be correct because IL Lags being Inductive where Ic Leads being Capactive so you have to have (IL - Ic) or (Ic - IL).
I just edited this as I had some silly errors!
Cheers
In your equations you get IT = 46.06A.
Using the following calculation I seem to get a different number.
(I1= 23A, I2 = 30.9A, I3 = 13.52A)
IT = sqrt I1^2 + (I2 - I3)^2
= sqrt 23^2 + 30.9-13.52^2
= sqrt 529 + 302
= sqrt 831
= 28.8A
Could you have a look & see what you think, I think this may be correct because IL Lags being Inductive where Ic Leads being Capactive so you have to have (IL - Ic) or (Ic - IL).
I just edited this as I had some silly errors!
Cheers
Last edited:
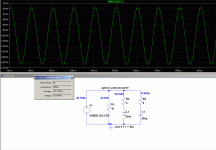
LTspice lets you quickly measure and calculate currents and (active) powers, so that you can easily check your calculations.
Here for instance, the total active power is 10.141KW (Alt + left click on V1, then Ctrl + left-click on the waveform name) (the display window has to be a multiple of the period)
Here for instance, the total active power is 10.141KW (Alt + left click on V1, then Ctrl + left-click on the waveform name) (the display window has to be a multiple of the period)
Attachments
Elvee,
can LTspice be asked for the two power values? the 10.5kW & the 10.2kW.
I think your first question and answer are the accurate value of 10.14kW for the lower power of 10.2kW.
can LTspice be asked for the two power values? the 10.5kW & the 10.2kW.
I think your first question and answer are the accurate value of 10.14kW for the lower power of 10.2kW.
Irakli,
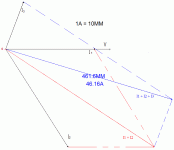
I have just drawn a Phasor diagram which I will attach to see if firstly if I could & then to see how things added up by using this method.
Your math is correct by the look of it, my calculation above would be correct only with a Purely Inductive & Capacitive Impedance or maybe I should say Inductive Reactance & Capacitive Reactance in that case XL & XC ?.
Then there would be a 90deg current Lag for the Inductive Part & A 90deg Lead for the Capacitive part. You would have to subtract one from the other in that case only.
From the Phasor diagram I get 46.16A which is very close to what you said & what LTSpice says.
I think I have the Phasor diagram drawn correctly if anyone can see I haven't done it correctly could they let me know please.
Elvee,
Yes LTSpice is a great Tool, I use it a lot but am still just learning about all this so any hints etc are greatly appreciated.
Cheers
I have just drawn a Phasor diagram which I will attach to see if firstly if I could & then to see how things added up by using this method.
Your math is correct by the look of it, my calculation above would be correct only with a Purely Inductive & Capacitive Impedance or maybe I should say Inductive Reactance & Capacitive Reactance in that case XL & XC ?.
Then there would be a 90deg current Lag for the Inductive Part & A 90deg Lead for the Capacitive part. You would have to subtract one from the other in that case only.
From the Phasor diagram I get 46.16A which is very close to what you said & what LTSpice says.
I think I have the Phasor diagram drawn correctly if anyone can see I haven't done it correctly could they let me know please.
Elvee,
Yes LTSpice is a great Tool, I use it a lot but am still just learning about all this so any hints etc are greatly appreciated.
Cheers
Attachments
Last edited:
Elvee,
can LTspice be asked for the two power values? the 10.5kW & the 10.2kW.
I think your first question and answer are the accurate value of 10.14kW for the lower power of 10.2kW.
Basically, LTspice can provide directly actual physical quantities, and P, the active power is one of them (10.141KW).
But S, the apparent power has no physical existence: it is just a convention that we, humans, find convenient to use, and it isn't available as a native function.
However, LTspice can also do maths, and any arbitrary function could be programmed if needed.
Irakli,
I have just drawn a Phasor diagram which I will attach to see if firstly if I could & then to see how things added up by using this method.
Your math is correct by the look of it, my calculation above would be correct only with a Purely Inductive & Capacitive Impedance or maybe I should say Inductive Reactance & Capacitive Reactance in that case XL & XC ?.
Then there would be a 90deg current Lag for the Inductive Part & A 90deg Lead for the Capacitive part. You would have to subtract one from the other in that case only.
From the Phasor diagram I get 46.16A which is very close to what you said & what LTSpice says.
I think I have the Phasor diagram drawn correctly if anyone can see I haven't done it correctly could they let me know please.
Elvee,
Yes LTSpice is a great Tool, I use it a lot but am still just learning about all this so any hints etc are greatly appreciated.
Cheers
Hi Again,
Your vector (phasor) diagram is correct. That's the right way to do things. By the way, complex numbers are nothing more (for our purposes) then another representation of these vectors. 🙂
One advice if I may.
I strongly recommend not to use simulators at all at this stage and do everything with paper, pencil and simple scientific calculator.
first, with simple circuits the math is not complicated. Most importantly, you will learn how things really work (good example is right here spending time with vector diagrams and understanding phase relationships). Also you will learn how to break big problem to smaller ones and isolate the essential things. All this is called good engineering and you can't learn it relaying on simulators. 🙂
Hi Irakli,
Yes, I understand what you mean about learning the math etc, this is a good example, I didn't quite understand until I drew the Phasor-Vector diagram.
I am happy I got it correct as it helped me a lot, I am trying to learn some complex math along the way & using the phasor diagrams may help me with this also.
I also understand that using programs to work things out for you can hinder the full understanding of things, that's why I thought it best to ask for some help to work this out properly.
Thanks for your help with this, I learnt a lot from this, I also learnt how much I don't know🙁
Thanks again
Elvee,
Yes I understand what your saying about LTSpice, I think I also have to learn how to do the math etc to be able to use this correctly as well.
It's all very interesting, I only wish I had learnt more some years ago.
Thanks everyone,
I actually learnt something😎
Cheers
Yes, I understand what you mean about learning the math etc, this is a good example, I didn't quite understand until I drew the Phasor-Vector diagram.
I am happy I got it correct as it helped me a lot, I am trying to learn some complex math along the way & using the phasor diagrams may help me with this also.
I also understand that using programs to work things out for you can hinder the full understanding of things, that's why I thought it best to ask for some help to work this out properly.
Thanks for your help with this, I learnt a lot from this, I also learnt how much I don't know🙁
Thanks again

Elvee,
Yes I understand what your saying about LTSpice, I think I also have to learn how to do the math etc to be able to use this correctly as well.
It's all very interesting, I only wish I had learnt more some years ago.
Thanks everyone,
I actually learnt something😎
Cheers
Elvee,
Yes I understand what your saying about LTSpice, I think I also have to learn how to do the math etc to be able to use this correctly as well.
It's all very interesting, I only wish I had learnt more some years ago.
Remember what I wrote:
LTspice lets you quickly measure and calculate currents and (active) powers, so that you can easily check your calculations.
I suggest you use it as a means of control after you've done the maths.
Just playing aimlessly with it won't be of any good.
- Status
- Not open for further replies.
- Home
- General Interest
- Everything Else
- True Power-- Math Question