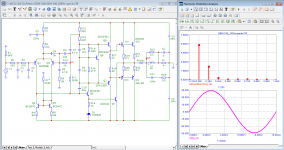
Note the loop gain - it is constant throughout the audio range. This guarantees a constant output impedance over the entire audio range and a constant distortion spectrum.If you don't mind me asking, what does the distortion spectrum look like at 100Hz?
Attachments
That was always clear TNT.
A hint to answer the questions posed in #19 is that:
For any symmetric input stimulus that traverses up and down the same upper or lower half of the transfer curve requires that the shape of the non-linearity be symmetric around the peaks of the input. In the case of a sinusoidal input this places the peaks of the second and third harmonic in line with the peak of the input sinusoid.
A hint to answer the questions posed in #19 is that:
For any symmetric input stimulus that traverses up and down the same upper or lower half of the transfer curve requires that the shape of the non-linearity be symmetric around the peaks of the input. In the case of a sinusoidal input this places the peaks of the second and third harmonic in line with the peak of the input sinusoid.
Just so you know, that was aimed at petr_ hence the suggestion for the name...
Syn08 could actually be a contender for a guru for me 🙂
//
Sure TNT. To be clear I also have great respect for petr_
You state this like it's a good thing. Why?Note the loop gain - it is constant throughout the audio range. This guarantees a constant output impedance over the entire audio range and a constant distortion spectrum.
It is known that there is a poor correlation between THD and sound quality.
A rising output impedance is like having an inductor in series with the output. The speaker cable has inductance and the speaker is highly inductive too.
What is your reasoning?
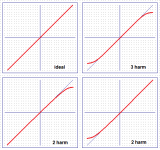
for clarity, your questions can be answered graphicallyIn the quest for a guru, perhaps as yourself:
There are four basic types of curved transfer function shapes of an amplifier being in relation to the midpoint of an input stimulus.
1. Upward expansive/Downward expansive
2. Upward compressive/Downward compressive
3. Upward expansive/Downward compressive
4. Upward compressive/Downward expansive
One and two generate third harmonics, three and four generate second harmonics. So the question is:
1. What is the wave shape and position of the non-linearity alone (in the time domain) resulting from a sinusoidal input stimulus that only generates a second harmonic in the frequency domain?
2. Under the same circumstances, that only generates a third harmonic?
asymmetric compression and expansion will lead to a wide range of harmonics
Attachments
Last edited: