Hi Friends!!
I have recently came across a text of impedance transformation provided by a tapped capacitor arrangement.
Its a rare and unique text explaining the working of tapped capacitor network in terms of conservation of power.
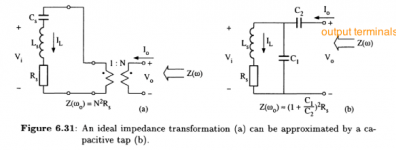
figure 6.31a) is an untapped case when no tapped capacitor is used..fig 6.31b) uses a tapped capacitor network(C1&C2)
The law of power conservation states that..If the magnitude of the power of an individual component in a circuit increases to a certain amount then there should be some compensatory change by the same amount in power of another component to maintain the overall power of the circuit constant.
In case I IL and Vi is constant, in second figure with use of tapped cap. Vi and IL changes which decreases the output current Io and increases the output voltage Vo, hence the latter can be thought of as increase in impedance.
Case 1 Vi and IL constant and power is conserved, whereas in case 2 Vi changes , IL changes which results in increase in Vo and Io,
My query is:-what kind of compensatory change is produced or observed when Vo and Io changes with the use of tapped capacitors, hence increasing the load impedance???
Thanks!!

I have recently came across a text of impedance transformation provided by a tapped capacitor arrangement.
Its a rare and unique text explaining the working of tapped capacitor network in terms of conservation of power.
figure 6.31a) is an untapped case when no tapped capacitor is used..fig 6.31b) uses a tapped capacitor network(C1&C2)
The law of power conservation states that..If the magnitude of the power of an individual component in a circuit increases to a certain amount then there should be some compensatory change by the same amount in power of another component to maintain the overall power of the circuit constant.
In case I IL and Vi is constant, in second figure with use of tapped cap. Vi and IL changes which decreases the output current Io and increases the output voltage Vo, hence the latter can be thought of as increase in impedance.
Case 1 Vi and IL constant and power is conserved, whereas in case 2 Vi changes , IL changes which results in increase in Vo and Io,
My query is:-what kind of compensatory change is produced or observed when Vo and Io changes with the use of tapped capacitors, hence increasing the load impedance???
Thanks!!


this example is typical for resonant networks, like wirelesscharging circuits.
so only valid at one frequency.
so only valid at one frequency.
These situations are more conventionally handled by using parallel-series impedance conversions, but the algebra can quickly get complicated. Conservation of energy can provide a shortcut.
impedance transformation provided by a tapped capacitor arrangement. Its a rare and unique
This is a TUNED circuit. The impedance transformation works over a -narrow- range of frequencies around resonance. Typically less than 3:1, or say 500Hz-1500Hz. Not a 1000:1 broadband transformation like we need in audio.
This is one of the classic ways to match transmitters to antennas, or to match radio IF coils into transistors.
image
You might want to learn to use a Smith chart if you're doing this sort of stuff much.
Networks of individual capactors and inductors only work narrow-band for impedance conversion, you need a transformer or resistor-divider for broadband conversion, only a transformer can do broadband low-loss impedance conversion.
Scope probe x10 mode is an interesting case related to capacitive networks, in that a resistor divider and a capacitor divider are working in parallel. Typical scope probes have about 50pF in x1 mode and 5pF in x10 mode. The impedance of the capacitive divider drops with frequency, so its not a broadband impedance converter, but it does act as a broadband voltage divider (for a low enough source resistance). Without it the x10 probe's response would roll-off from about 3kHz whatever the source impedance.
Networks of individual capactors and inductors only work narrow-band for impedance conversion, you need a transformer or resistor-divider for broadband conversion, only a transformer can do broadband low-loss impedance conversion.
Scope probe x10 mode is an interesting case related to capacitive networks, in that a resistor divider and a capacitor divider are working in parallel. Typical scope probes have about 50pF in x1 mode and 5pF in x10 mode. The impedance of the capacitive divider drops with frequency, so its not a broadband impedance converter, but it does act as a broadband voltage divider (for a low enough source resistance). Without it the x10 probe's response would roll-off from about 3kHz whatever the source impedance.
These situations are more conventionally handled by using parallel-series impedance conversions, but the algebra can quickly get complicated. Conservation of energy can provide a shortcut.
Could you please elaborate what kind of shortcut does it provide..I don't get it..
Conservation of energy can lead to simpler algebra. However, you need to be careful if the circuit includes resistance because that will dissipate energy, or a power source because that will injuect energy. Use whatever technique seems best to you.
For the particular circuit you showed us the parallel-series impedance transformation may be the simplest technique to use.
For the particular circuit you showed us the parallel-series impedance transformation may be the simplest technique to use.
For the particular circuit you showed us the parallel-series impedance transformation may be the simplest technique to use.
Let me be more clear...
In fig 6.31a) IL and Vi is constant and in fig 6.31b) due to presence of two capacitors IL and Vi changes hence reducing the the output current Io and increasing the externally required voltage (i.e output voltage Vo) underlined. So my question is why this external voltage increases which is technically equal to increase in impedance...Is it a compensatory change just in order to conserve power in circuit..??
No, IL and Vi are names for a complex current and a complex voltage, not constants.Let me be more clear...
In fig 6.31a) IL and Vi is constant
and in fig 6.31b) due to presence of two capacitors IL and Vi changes hence reducing the the output current Io and increasing the externally required voltage (i.e output voltage Vo) underlined. So my question is why this external voltage increases which is technically equal to increase in impedance...Is it a compensatory change just in order to conserve power in circuit..??
In both diagrams the impedance at resonance is given by the formulae (w0 is the resonant angular frequency, 1/√LC). At resonance the L and C impedances cancel exactly. In (a) this means they act as a short circuit at resonance, in (b) the tap between L and C prevents this cancelation, its takes a bit of algebra to figure out the formula.
There's nothing technical about it, the impedance is a measurable physical quantity. The formulae for computing impedance of a network are just like at DC, but with complex impedance values that are functions of frequency.
It is a compensatory change in order to preserve the same power in the circuit.brainbaby said:Is it a compensatory change just in order to conserve power in circuit..??
in (b) the tap between L and C prevents this cancelation, its takes a bit of algebra to figure out the formula.
Could you please elaborate your point.."tap prevents cancellation..."
I am thinking this way....the parallel RC combination is transformed into series equivalent with a new value of Rs and new value of capacitance (C1//C2)...let say Ceq..which is in series with Ls due to parallel to series conversion..
Now as per your statement the tap prevent the cancellation of impedance of reactive components at resonance...so it implies that Ceq and Ls will have some impedance (which won't cancel)and will contribute to some power dissipation in the circuit along with Rs.
So mathematically Power = VI and in case b) Vo*Io = individual power dissipation along Ls,Ceq and Req..(as with the absence of the tap, Power dissipation of circuit (Vo*Io) will be equal to power dissipation among Rs only............your comments...
Yes it feels better to me hearing what I expected...but the problem is its an assumption ....not proved yet..It is a compensatory change in order to preserve the same power in the circuit.
I am still not sure whats that compensatory change is...may be its the increase in the output voltage...If the output voltage is increase then there might be something in Ls Ceq or Req.. that might have changed.....and in order to balance it Vo has increased
but first lets see what Mark has to comment...then see where the discussion goes..
C and L do not dissipate power, they merely store it for a while. Only R can dissipate power.
Adding the extra capacitor between the tuned circuit and the outside world can be considered to reduce the coupling between them. It increases the external voltage needed to get a particular internal current going.
From this distance it is difficult to peer inside your head and see exactly what it is that puzzles you. We don't know what assumptions you are making, so we cannot know which of them are right and which are wrong. We don't know at what level you are thinking about electronics: absolute beginner who is struggling to understand any circuit and so is trying to run before he can walk, experienced amateur who has just encountered energy conservation as a circuit analysis technique for the first time etc.
Adding the extra capacitor between the tuned circuit and the outside world can be considered to reduce the coupling between them. It increases the external voltage needed to get a particular internal current going.
From this distance it is difficult to peer inside your head and see exactly what it is that puzzles you. We don't know what assumptions you are making, so we cannot know which of them are right and which are wrong. We don't know at what level you are thinking about electronics: absolute beginner who is struggling to understand any circuit and so is trying to run before he can walk, experienced amateur who has just encountered energy conservation as a circuit analysis technique for the first time etc.
C and L do not dissipate power, they merely store it for a while. Only R can dissipate power.
Adding the extra capacitor between the tuned circuit and the outside world can be considered to reduce the coupling between them. It increases the external voltage needed to get a particular internal current going
.
I got your point...Actually due to the presence of capacitive network current divides and reduces in the output branch. Power equals VI, hence I changed here and to maintain a constant power V changed to the same amount, this amount depends upon the ratio of capacitances (which varies the current in the circuit).
- Home
- Amplifiers
- Solid State
- Tapped capacitor impedance matching along with power conservation..?