I remember this problem as an analogy to another problem. In a network of roads the traffic jam problem increases when one more road is added between 2 intersections.
Yes... I nearly posted the same comment. It was a long long time ago. ETI or WW ? Not sure if it was in the same article but I vaguely remember something about modelling a road network with resistors, the current flow being equal to traffic density. When a low impedance was added between two nodes the current flow decreases...... hmmm 😉
It can be done much simpler and more effective.
Yes that is almost the answer I think Mark was looking for. (Bottom needs just a bit of slack.) But JN had a viable solution also, just not as magical appearing.
Last edited:
I have posted what I consider to be the best solution; I edited it into post #1 at the top of this thread. Follow the link and read the paper.
Simon,
What kind of slack do you think of and why needed? And which post of JN?
You only need enough slack initially to be sure the springs are in series. JN post 11.
My feel is this was the equivalent of the question "How do you measure the height of a building using a mercury barometer?"
But mark it was a bit of a brain teaser and fun.
You only need enough slack initially to be sure the springs are in series. JN post 11.
My feel is this was the equivalent of the question "How do you measure the height of a building using a mercury barometer?".
That's simple.
Measure the barometric pressure at the bottom very carefully.
Next, take it to the top of the building, and again measure the pressure very carefully.
Using those two different pressures, throw the barometer off the top of the building and time how long it takes to hit the ground.
Calculate the distance using that time, the equation is d = 1/2 At^2.
If you need more accuracy, include the barometric pressure and it's gradient.
One thing wrong with that paper, is that the figure 1 drawing is terribly inaccurate. If you examine their after drawing, they show the nodes formerly held by the center string as being closer together. Obviously incorrect, as each spring would be shorter after the cut. If you're gonna model something, at least make the drawings accurate....sigh
John
Last edited:
Measure the length of the shadow of the barometer. Measure the length of the shadow of the building. Measure the height of the barometer. Using similar triangles calculate the height of the building
(Bldg_height / barometer_height) = (Bldg_shadow_length / barometer_shadow_length)
{here is a link to the 1964 original}
(Bldg_height / barometer_height) = (Bldg_shadow_length / barometer_shadow_length)
{here is a link to the 1964 original}
Series springs was not a requirement. (My 1st solution didn't use series springs.) I still don't know what 'slack' means for you in this context. I checked in dictionary, but such a huge number of different meaning I saw I totally was unable to understand what you wanted to tell. Too weak word to describe a technical situation by itself.
Post 11 is also hard to understand to me, many details are not stated, others are ambiguous, but if I understood correctly, then it works only if the relaxed spring is more stiff than the tensed. At extreme: one spring can be replaced by string.
Post 11 is also hard to understand to me, many details are not stated, others are ambiguous, but if I understood correctly, then it works only if the relaxed spring is more stiff than the tensed. At extreme: one spring can be replaced by string.
Translating the problem into electronic circuitry gives this discussion thread here on diyAudio. In my experience, people seem to find the electronic version more difficult than the mechanical version, for some reason.
Post 11 is also hard to understand to me, many details are not stated, others are ambiguous, but if I understood correctly, then it works only if the relaxed spring is more stiff than the tensed. At extreme: one spring can be replaced by string.
Can't stand it. I rotated it on my computer, it went back here..sigh.
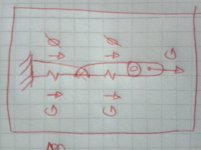
As drawn, spring A is bearing all the weight because I added a string from the weight to the A spring to string node.
Spring B is relaxed because the string from A to B allows it to relax.
Cut the link, and spring A will go up, it will pull B down. When equilibrium is established, A and B will share the weight.
If the string between A and B is sized correctly, the weight will climb exactly half the distance between the A and B nodes as drawn when the link is cut.
John
Attachments
Last edited:
This is an old problem. Many years ago, one of my sons demonstrated the effect for a 6th grade science fair project. Unfortunately, it ended up confusing his teacher. Anyway, for each spring (or rubber band) f=-kx (from 1st year physics of mechanics). Depending on k for the springs, f needed to support the weight, and the displacement x in both cases, string cut or un-cut, you can design it to lift when the string is cut.
Last edited:
Can't stand it. I rotated it on my computer, it went back here..sigh.
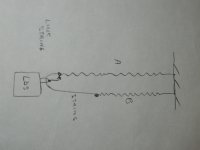
As drawn, spring A is bearing all the weight because I added a string from the weight to the A spring to string node.
Spring B is relaxed because the string from A to B allows it to relax.
Cut the link, and spring A will go up, it will pull B down. When equilibrium is established, A and B will share the weight.
If the string between A and B is sized correctly, the weight will climb exactly half the distance between the A and B nodes as drawn when the link is cut.
John
Are you sure? The sum of the forces seen by A and B is constant. If elasticities are the same, then any force difference will cause the same amount of contraction and expansion in the strings, therefore the height remains. You need stiffer right spring. The stiffest is the string. And this way one can easily see whats going on basically. The length of string has no role at all.
This is an old problem. Many years ago, one of my sons demonstrated the effect for a 6th grade science fair project. Unfortunately, it ended up confusing his teacher.
If it happened more than 25 years ago, you need to contact the editors of Nature and tell them they made a mistake when they accepted it for publication in 1991. The .pdf even gives the exact date when the manuscript was received; if you've still got your day planner notebooks from that era you could check to see what day your son's 6th grade science fair was held.
Are you sure? The sum of the forces seen by A and B is constant. If elasticities are the same, then any force difference will cause the same amount of contraction and expansion in the strings, therefore the height remains. You need stiffer right spring. The stiffest is the string. And this way one can easily see whats going on basically. The length of string has no role at all.
I assumed the springs are linear. 10 lbs will cause twice the extension of 5 lbs.
If I use 1 inch per lb as a constant, spring A will drop 10 inches under full weight. If I make the A to B string 10 inches long, it will just be straight, with no pull on it.
When I cut the link, spring A will rise up, the string will slip through the loop at the weight, and it will pull down on spring B. When both A and B have the same weight, they will be 5 inches extension each.....oops...
D###. I think you are right, I'm wrong..😱
But still, a nice puzzle...
John
If it happened more than 25 years ago, you need to contact the editors of Nature and tell them they made a mistake when they accepted it for publication in 1991. The .pdf even gives the exact date when the manuscript was received; if you've still got your day planner notebooks from that era you could check to see what day your son's 6th grade science fair was held.
Actually, it was roughly from around 25 years ago, although I was not aware of the Nature article. It's possible I read about the paradox from some popular press article playing up the Nature article. The solution was not given wherever I saw it though. After I worked out the math for a simple geometry case it seemed so trivial that we left the presentation a little more mysterious sounding for the science fair, which in hindsight was too mysterious for the teacher.
John,
Thanks for the clarification, and don't feel bad, your solution was usable, just needed some refinement. And valuable, because different.
Thanks for the clarification, and don't feel bad, your solution was usable, just needed some refinement. And valuable, because different.
JN
I though you understood a steel spring in normal use is a torsional device thus reasonably linear force vs stretch. A rubber band gets thinner as you stretch it so it is not linear force vs distance.
So you are correct in asserting you erred. But it was not the solution's design, rather in believing it wouldn't work.
Then you can offer the barometer as a prize for whoever can accurately give you the building's height.
Then again I think some folks really grow roses for the thorns.
I though you understood a steel spring in normal use is a torsional device thus reasonably linear force vs stretch. A rubber band gets thinner as you stretch it so it is not linear force vs distance.
So you are correct in asserting you erred. But it was not the solution's design, rather in believing it wouldn't work.
Then you can offer the barometer as a prize for whoever can accurately give you the building's height.
Then again I think some folks really grow roses for the thorns.
Last edited:
John,
Thanks for the clarification, and don't feel bad, your solution was usable, just needed some refinement. And valuable, because different.
Nah, I was just incorrect in my thinking. It became clear as I was typing a verbal explanation...
JN
I though you understood a steel spring in normal use is a torsional device thus reasonably linear force vs stretch. A rubber band gets thinner as you stretch it so it is not linear force vs distance.
So you are correct in asserting you erred. But it was not the solution's design, rather in believing it wouldn't work.
Then you can offer the barometer as a prize for whoever can accurately give you the building's height.
Then again I think some folks really grow roses for the thorns.
I assumed linearity. Non linear elastic behavior is not what the experiment was trying to show.
So we finally agree on something, eh? That I was in error...😉
John
- Status
- Not open for further replies.
- Home
- Member Areas
- The Lounge
- Rubber bands + string hoist a weight. Cut a string, the weight *rises* (!!)