A worst-case assumption is six values uniformly distributed from 99 to 101 inclusive - that's five divisions starting a t 99 and incrementing by 2/5 of an ohm:
Code:
99.0
99.4
99.8
100.2
100.6
101.0What I'm wondering is why you don't buy 100 or 250 resistors and have a bunch extra in stock for other projects, as they're around a cent (0.01 USD) each. With that you can number each resistor (just put them in a cardboard edge or somehow kept separate left to right), measure each and put its value in a spreadsheet with each number, and sort both fields by resistance, as I show below. You'll get dozens of pairs that are arbitrarily close.
They certainly match better than a UNIFORM spread would indicate!
So I put these into LibreOffice Calc (much like Excel but a lot less expensive) and numbered each:
Code:
1 9965
2 9974
3 9969
4 9953
5 9959
6 9944
7 9956
8 9952
9 9963
10 9961
11 9969
12 9979
13 9971
14 9992
15 9964
16 9953
17 9954
18 9966
19 9948
20 9968
21 9953
22 9970
23 9996
24 9961
25 9932
26 9961
27 9971
28 9953
29 9956
30 10005
Code:
25 9932
6 9944
19 9948
8 9952
4 9953
16 9953
21 9953
28 9953
17 9954
7 9956
29 9956
5 9959
10 9961
24 9961
26 9961
9 9963
15 9964
1 9965
18 9966
20 9968
3 9969
11 9969
22 9970
13 9971
27 9971
2 9974
12 9979
14 9992
23 9996
30 10005
Last edited:
Here's a dump of the first 200 Monte Carlo trials. The six resistor values are printed (in sorted order for ease of reading), then the best match. If the best match is less than or equal to 0.05%, an E (for Excellent) is printed. In those 200 trials, 113 were Excellent, which is 56.5%. Not 93%.
All 200*6 = 1200 random numbers are included in the dump. If you sort them and plot the data, you see a straight line, just as expected from uniformly distributed random numbers.
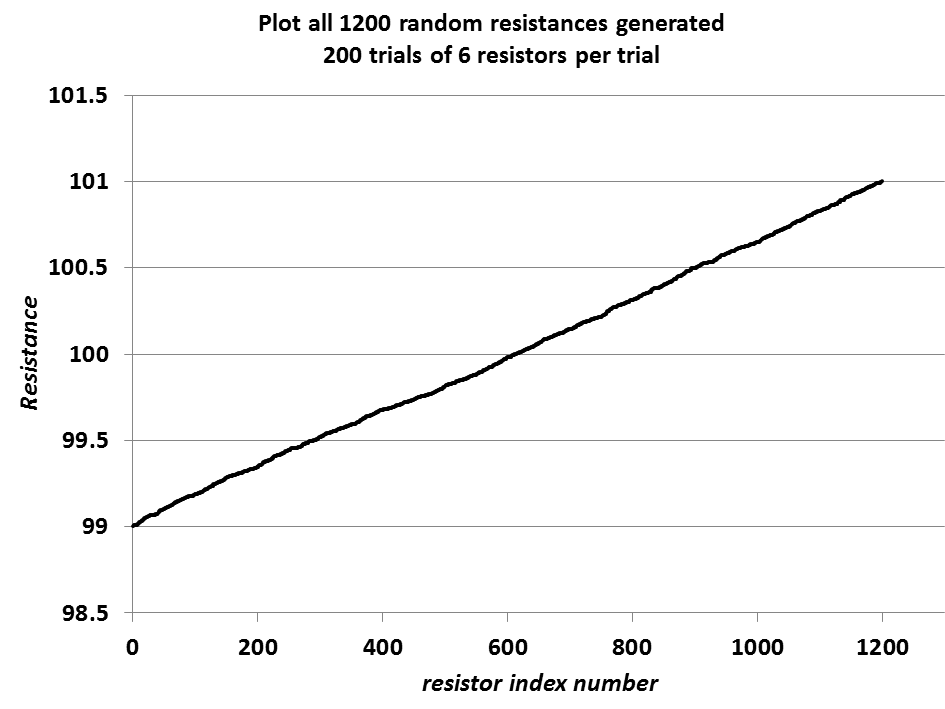
All 200*6 = 1200 random numbers are included in the dump. If you sort them and plot the data, you see a straight line, just as expected from uniformly distributed random numbers.
Code:
99.07111 99.30365 99.71210 100.00867 100.27026 100.28345 match 0.0131 % E
99.00482 99.73438 100.20691 100.35260 100.75793 100.77838 match 0.0203 % E
99.09967 99.67633 99.87744 99.99481 100.26343 100.53802 match 0.1175 %
99.17236 99.37695 99.71698 100.37799 100.38153 100.76239 match 0.0035 % E
99.21002 99.42523 100.10388 100.14465 100.31165 100.50635 match 0.0407 % E
99.13080 99.78918 99.84540 100.13922 100.21204 100.62372 match 0.0563 %
99.25842 99.52063 99.53174 100.14014 100.21387 100.50153 match 0.0112 % E
99.57397 99.58246 99.63226 99.85870 100.58478 100.67273 match 0.0085 % E
99.06421 99.25861 99.26569 99.47308 100.01862 100.19611 match 0.0071 % E
99.70068 99.95331 100.03412 100.38593 100.67743 100.84027 match 0.0808 %
99.00525 99.45300 100.44885 100.57257 100.61652 100.75653 match 0.0437 % E
99.44000 99.49170 99.98132 100.08295 100.45990 100.93890 match 0.0520 %
99.62115 99.71924 100.08850 100.19873 100.58374 100.64917 match 0.0650 %
99.04419 99.14777 100.12183 100.13940 100.61829 100.78668 match 0.0176 % E
99.20123 99.33636 99.62628 100.34174 100.47906 100.59332 match 0.1137 %
99.24426 99.41443 99.81775 99.93280 99.93964 100.64435 match 0.0068 % E
99.35938 99.70856 99.84521 99.89948 100.24615 100.49585 match 0.0543 %
99.59937 99.69037 99.69720 99.97784 100.28168 100.77576 match 0.0069 % E
99.07489 99.22076 99.48834 99.82965 100.00348 100.11731 match 0.1138 %
99.11249 99.54388 100.25183 100.35199 100.57104 100.89215 match 0.0999 %
99.03516 99.18512 99.29114 99.89069 100.31665 100.39838 match 0.0815 %
99.34827 99.39423 99.44098 100.20227 100.68274 100.68433 match 0.0016 % E
99.17938 99.28320 99.38654 99.64807 100.20972 100.62683 match 0.1041 %
99.16144 99.56116 99.74603 100.20630 100.21112 100.43176 match 0.0048 % E
99.09338 99.49188 99.61292 100.11505 100.51563 100.68317 match 0.1217 %
99.57080 99.79596 100.21466 100.25934 100.80493 100.93097 match 0.0446 % E
99.02502 99.11969 99.16742 99.16974 99.90485 100.41760 match 0.0023 % E
99.75793 99.85071 99.87537 100.35968 100.43048 100.86639 match 0.0247 % E
99.00507 99.45166 99.98035 100.39374 100.54822 100.57703 match 0.0287 % E
99.33368 99.37823 99.92041 99.93555 100.71741 100.76538 match 0.0151 % E
99.86438 100.20526 100.68689 100.70563 100.86725 100.95825 match 0.0186 % E
99.06360 99.49585 99.51489 100.27594 100.29071 100.96771 match 0.0147 % E
99.05084 99.06683 99.47504 100.08203 100.16565 100.62476 match 0.0161 % E
99.13153 99.30865 99.45160 99.54321 99.57190 100.42572 match 0.0288 % E
99.29840 100.01532 100.12988 100.37708 100.72632 100.88873 match 0.1145 %
99.17657 99.24255 99.54840 100.58478 100.70288 100.85938 match 0.0665 %
99.37653 99.40808 99.92303 100.51794 100.76324 100.91260 match 0.0318 % E
99.02057 99.03003 99.32312 99.41132 100.49939 100.57019 match 0.0096 % E
99.15515 99.17395 99.59271 100.11029 100.71936 100.95599 match 0.0190 % E
99.52563 99.66992 99.80591 100.02863 100.09198 100.32507 match 0.0633 %
99.30676 99.31506 100.09460 100.24689 100.73242 100.82416 match 0.0084 % E
99.19934 100.01331 100.54498 100.61798 100.78265 100.83527 match 0.0522 %
99.18921 99.42377 99.48108 99.51813 99.66431 99.88959 match 0.0372 % E
99.02594 99.15540 99.49268 99.87921 99.97400 100.18768 match 0.0949 %
99.48291 99.58972 99.60236 99.99445 99.99982 100.34668 match 0.0054 % E
99.58240 99.58661 100.08160 100.23151 100.34338 100.41846 match 0.0042 % E
99.05511 99.46564 99.72253 100.38129 100.52643 100.62439 match 0.0974 %
99.16840 99.22900 99.35278 99.90997 100.11090 100.99524 match 0.0611 %
99.32300 99.53986 99.57062 99.66498 100.98218 100.99054 match 0.0083 % E
99.04492 99.06512 99.27325 99.84222 100.26898 100.89508 match 0.0204 % E
99.29761 99.94519 100.05933 100.22937 100.79749 100.86810 match 0.0701 %
99.18311 99.43286 99.82550 99.90851 100.13312 100.62988 match 0.0832 %
99.10010 99.46759 99.49872 100.03058 100.60754 100.69696 match 0.0313 % E
99.26569 99.41144 99.63007 100.12384 100.54102 100.80298 match 0.1468 %
99.57629 99.69794 100.39966 100.60931 100.86017 100.94409 match 0.0832 %
99.26355 99.39270 100.53357 100.64459 100.70227 100.81403 match 0.0573 %
99.37115 99.46027 99.46173 99.75763 100.41339 100.83875 match 0.0015 % E
99.14642 99.37982 99.48468 99.79327 99.86505 100.30847 match 0.0719 %
99.87128 99.95123 100.41431 100.49524 100.55786 100.60425 match 0.0461 % E
99.25586 99.58447 99.76764 100.08411 100.48505 100.90460 match 0.1839 %
99.05054 99.33008 99.72156 99.74835 99.82849 100.02008 match 0.0269 % E
99.14154 99.44751 99.91742 100.01178 100.64313 100.81879 match 0.0944 %
99.79767 99.84686 99.90594 100.03210 100.57373 100.99725 match 0.0493 % E
99.35724 99.52515 99.70270 99.91742 100.87769 100.95618 match 0.0778 %
99.21143 99.28760 99.43787 100.38733 100.45667 100.90710 match 0.0691 %
99.83105 99.94586 99.95715 100.37836 100.80487 100.92395 match 0.0113 % E
99.33551 99.41571 99.54889 99.65857 99.85071 100.47772 match 0.0807 %
99.12152 99.72620 99.78070 99.81946 99.97919 100.06830 match 0.0388 % E
99.40497 99.41486 99.72479 99.77350 100.40662 100.86414 match 0.0099 % E
99.59039 99.63904 99.73096 99.82458 99.82593 100.25769 match 0.0013 % E
99.09241 99.50067 99.62549 99.96539 99.98395 100.73029 match 0.0186 % E
99.17560 99.38324 99.98096 100.09430 100.18475 100.89215 match 0.0904 %
99.17334 99.20221 99.24512 99.25317 99.75311 100.86188 match 0.0081 % E
99.02277 99.47968 99.94104 100.45929 100.67957 100.70776 match 0.0280 % E
99.30365 99.44415 100.59857 100.62402 100.77094 100.82819 match 0.0253 % E
99.13940 99.72382 99.75146 100.11267 100.44702 100.65552 match 0.0277 % E
99.18591 99.42517 99.75305 100.11810 100.81818 100.98950 match 0.1699 %
99.16132 99.32977 99.56311 100.68439 100.82605 100.86139 match 0.0350 % E
99.49506 99.96869 100.49866 100.59027 100.75891 100.84796 match 0.0884 %
99.09137 99.12494 99.52094 100.45624 100.67786 100.94250 match 0.0339 % E
99.67596 99.69336 99.76367 99.76807 100.17163 100.18359 match 0.0044 % E
99.00824 99.18640 99.90985 100.04565 100.06592 100.14484 match 0.0203 % E
99.15247 99.62836 100.08545 100.17560 100.69543 100.86200 match 0.0901 %
99.22180 99.45465 99.89197 100.12268 100.98254 100.98907 match 0.0065 % E
99.06464 99.50360 99.73682 100.50214 100.58954 100.66370 match 0.0737 %
99.11951 99.17322 99.22620 99.29755 100.33240 100.96600 match 0.0534 %
99.31824 99.32349 100.06531 100.12152 100.64246 100.71875 match 0.0053 % E
99.67078 99.72089 99.77618 100.36884 100.64520 100.65375 match 0.0085 % E
99.57794 99.92657 100.15912 100.30969 100.51141 100.84589 match 0.1503 %
99.28680 99.50806 99.67621 99.70758 100.28271 100.85510 match 0.0315 % E
99.11908 99.19446 99.82031 100.33258 100.38721 100.54456 match 0.0544 %
99.04852 99.06464 99.37604 99.79620 100.13403 100.75366 match 0.0163 % E
99.29962 99.80615 100.31091 100.40527 100.93024 100.94543 match 0.0151 % E
99.30560 99.33002 99.38757 99.51117 100.20477 100.63470 match 0.0246 % E
99.97131 100.10571 100.18494 100.42004 100.52307 100.95038 match 0.0791 %
99.28040 99.73236 100.32397 100.32410 100.32562 100.33246 match 0.0001 % E
99.17670 99.32025 99.65851 100.23712 100.33508 100.61353 match 0.0977 %
99.25848 99.29242 99.63702 99.68585 99.85754 100.41534 match 0.0342 % E
99.53143 100.29480 100.49719 100.64728 100.72137 100.96027 match 0.0736 %
99.23242 99.43695 99.83923 99.99164 100.20654 100.93488 match 0.1527 %
99.11090 99.25128 99.61285 99.83887 100.08331 100.14056 match 0.0572 %
99.26434 100.14868 100.23840 100.65283 100.90070 100.91345 match 0.0126 % E
99.18774 99.58618 100.18890 100.19659 100.53156 100.94592 match 0.0077 % E
99.57672 99.99829 100.17432 100.17804 100.34912 100.38086 match 0.0037 % E
99.40918 99.67816 99.76416 99.98059 100.16412 100.71021 match 0.0863 %
99.03699 99.06030 99.31818 99.33417 100.09851 100.21948 match 0.0161 % E
99.41046 99.51465 99.57758 99.71460 100.07745 100.91656 match 0.0632 %
99.17474 99.19495 99.21338 99.78455 100.20483 100.37811 match 0.0186 % E
99.10297 99.24579 99.33228 99.38611 99.67377 100.71533 match 0.0542 %
99.05060 99.37146 99.59180 99.68854 100.00555 100.53253 match 0.0971 %
99.67755 99.76947 100.03381 100.14465 100.62555 100.87762 match 0.0922 %
99.14825 99.40051 99.59521 99.82147 100.01385 100.61731 match 0.1927 %
99.42267 99.43958 99.70013 99.85486 100.04498 100.67114 match 0.0170 % E
99.54102 100.04004 100.06067 100.31525 100.44867 100.61639 match 0.0206 % E
99.48425 99.96265 100.32129 100.59387 100.61353 100.61401 match 0.0005 % E
99.13660 99.21826 99.77203 99.90521 100.34802 100.70337 match 0.0824 %
99.64063 99.68420 99.72845 100.75317 100.75397 100.80707 match 0.0008 % E
99.64679 99.75623 99.87958 100.35364 100.69177 100.78058 match 0.0882 %
99.21613 99.24890 100.50702 100.80426 100.83331 100.92981 match 0.0288 % E
99.00037 99.34113 99.54291 99.74219 100.49347 100.61365 match 0.1196 %
99.00806 99.43665 99.54889 99.92151 100.05548 100.14832 match 0.0928 %
100.18463 100.39410 100.40350 100.47754 100.84387 100.87555 match 0.0094 % E
99.33569 99.34253 100.59216 100.63599 100.73193 100.82672 match 0.0069 % E
99.00543 99.07043 99.26111 100.05792 100.10583 100.12518 match 0.0193 % E
99.60620 99.61725 100.44568 100.52966 100.72784 100.79852 match 0.0111 % E
99.45081 99.45557 99.81445 100.05145 100.31750 100.97803 match 0.0048 % E
99.03229 99.55634 99.81830 99.89288 100.59662 100.79517 match 0.0747 %
99.14673 99.19220 99.45581 100.02594 100.46735 100.72906 match 0.0459 % E
99.07220 99.76361 99.87701 100.21002 100.68500 100.84039 match 0.1137 %
99.49536 100.28186 100.37360 100.40259 100.91223 100.96936 match 0.0289 % E
99.19403 99.56250 99.59296 100.92902 100.93567 100.96564 match 0.0066 % E
99.31683 99.87573 100.38110 100.84381 100.90936 100.93774 match 0.0281 % E
99.11145 99.29108 99.63586 99.75311 99.80511 100.92480 match 0.0521 %
99.01117 99.49811 99.72632 100.00818 100.30414 100.39197 match 0.0876 %
99.06537 99.60382 100.29675 100.35071 100.52887 100.97650 match 0.0538 %
99.55261 99.89227 99.94666 99.94971 100.11835 100.78760 match 0.0031 % E
100.11414 100.25818 100.28345 100.53113 100.74335 100.76587 match 0.0224 % E
99.10730 99.68091 99.68488 100.00629 100.02893 100.40369 match 0.0040 % E
99.64642 99.87372 100.15192 100.29236 100.43445 100.84119 match 0.1402 %
99.58386 99.84534 100.26770 100.29639 100.40735 100.88733 match 0.0286 % E
99.57031 99.70294 99.89105 100.44806 100.79547 100.88043 match 0.0843 %
99.59052 100.03827 100.21802 100.22430 100.63672 100.81519 match 0.0063 % E
99.49811 99.75494 100.15387 100.17609 100.70929 100.78918 match 0.0222 % E
99.34253 99.45093 99.56665 99.64246 100.57770 100.99530 match 0.0761 %
99.05988 99.30200 99.93677 100.04626 100.40991 100.97125 match 0.1096 %
99.38208 99.45367 100.52570 100.53137 100.59137 100.97473 match 0.0056 % E
99.54254 99.75763 100.43042 100.50958 100.64142 100.93475 match 0.0788 %
99.69653 99.74078 99.86493 99.97076 100.36597 100.44720 match 0.0444 % E
99.14941 99.65137 99.82233 100.43787 100.76611 100.76904 match 0.0029 % E
99.54889 99.85162 99.90283 100.52179 100.53113 100.73553 match 0.0093 % E
99.45721 99.80334 100.03601 100.20276 100.73730 100.79797 match 0.0602 %
99.32257 99.68134 99.82202 100.24402 100.29840 100.63727 match 0.0542 %
99.56555 99.70074 99.75769 99.85748 100.59595 100.71344 match 0.0571 %
99.33295 99.70923 100.22144 100.35938 100.61676 100.91180 match 0.1376 %
99.27911 99.74396 99.84833 100.28461 100.31512 100.77179 match 0.0304 % E
99.05847 99.65125 99.72729 100.63684 100.67151 100.90540 match 0.0344 % E
99.29645 99.41907 99.62170 99.87152 100.52515 100.82111 match 0.1235 %
99.32068 99.88586 100.27020 100.67194 100.77563 100.97363 match 0.1030 %
99.26398 99.67108 99.67609 99.83740 100.18866 100.52332 match 0.0050 % E
99.47430 99.67938 99.74701 99.78271 100.28601 100.92261 match 0.0358 % E
99.08490 99.30560 99.39160 100.55267 100.83368 100.86395 match 0.0300 % E
99.23303 99.30420 99.30945 99.84985 100.27026 100.82532 match 0.0053 % E
99.08551 99.66046 99.83063 100.57800 100.62311 100.74023 match 0.0448 % E
99.29034 99.52576 100.49554 100.49884 100.52936 100.73499 match 0.0033 % E
99.19843 99.23273 100.09924 100.10950 100.19122 100.48236 match 0.0102 % E
99.40417 99.55200 99.55231 99.63873 100.05273 100.46912 match 0.0003 % E
99.13531 99.78796 100.27484 100.55524 100.71106 100.88770 match 0.1550 %
99.13794 99.49164 99.65350 99.73657 99.82916 100.59259 match 0.0834 %
99.06586 99.57831 99.66113 100.14166 100.54846 100.98584 match 0.0832 %
99.22821 99.54248 99.99536 99.99762 100.67896 100.96637 match 0.0023 % E
99.33710 99.41119 99.50110 99.76208 99.86993 100.92279 match 0.0746 %
99.36395 99.56787 99.79150 99.87366 100.18951 100.26654 match 0.0769 %
99.10535 99.60614 99.67969 100.03668 100.05927 100.07220 match 0.0129 % E
99.45667 99.64459 100.20288 100.85883 100.95697 100.98975 match 0.0325 % E
99.28284 99.30841 99.79785 100.52606 100.59741 100.90356 match 0.0258 % E
99.82715 100.09607 100.63611 100.76874 100.89240 100.99121 match 0.0979 %
99.53442 99.59314 99.75085 99.77747 100.09326 100.30847 match 0.0267 % E
99.16028 99.23157 99.43549 100.05774 100.18671 100.68597 match 0.0719 %
99.09381 99.54657 99.76727 99.86908 100.18060 100.47070 match 0.1020 %
99.12122 99.21826 99.63873 99.96625 100.60760 100.82971 match 0.0979 %
99.35480 99.53998 99.60889 99.75397 99.77478 100.98737 match 0.0209 % E
99.28925 99.70990 100.16492 100.29004 100.37946 100.56714 match 0.0892 %
99.08612 99.47430 99.51599 99.69208 99.71942 100.08612 match 0.0274 % E
99.11230 99.45941 99.68341 100.02802 100.47638 100.85278 match 0.2252 %
99.15338 99.26501 99.67773 99.68579 100.00073 100.28754 match 0.0081 % E
99.70026 100.35944 100.45294 100.66681 100.81323 100.82709 match 0.0137 % E
99.09991 99.31354 100.01007 100.34418 100.52686 100.58563 match 0.0585 %
99.07349 99.29443 99.68402 100.35767 100.47858 100.57050 match 0.0915 %
99.01544 99.06445 99.95544 100.09186 100.20337 100.63013 match 0.0495 % E
99.16125 99.19543 99.37006 100.11749 100.29773 100.55811 match 0.0345 % E
99.84167 100.28833 100.31219 100.33893 100.44269 100.73688 match 0.0238 % E
99.15540 99.92175 99.93793 99.93970 100.51996 100.92975 match 0.0018 % E
99.92529 100.38135 100.47656 100.52313 100.83960 100.97125 match 0.0463 % E
99.20093 99.85236 100.14172 100.22101 100.93927 100.94855 match 0.0092 % E
99.35889 99.47504 99.71838 99.92261 100.17175 100.66846 match 0.1169 %
99.16919 99.55597 99.73138 99.83917 99.99390 100.49377 match 0.1081 %
99.31989 99.41608 100.14557 100.29883 100.71960 100.78699 match 0.0669 %
99.45575 99.88770 100.02142 100.15607 100.26971 100.85101 match 0.1135 %
99.97748 100.10083 100.16766 100.41888 100.64764 100.81287 match 0.0668 %
99.35419 99.45453 99.50610 99.75317 100.55884 100.57410 match 0.0152 % E
113 trials (out of 200) matched better than 0.05% (marked Excellent "E")Attachments
Last edited:
Sorry, I screwed it above, nothing to do with C(N-1,2)
1. Pull a resistor out of 6 (so 5 left). Since the probability in the [a, b] interval is uniform, any value is possible there. Let's call this value S1 (sample 1).
2. Around S1, consider an interval [a', b'] defined by the desired matching tolerance.
3. Pull another resistor with value S2 (4 left). S2 can also be anywhere in [a, b] with equal probability; the probability to fall in [a', b'] is P2=(b'-a')/(b-a).
4. The probability for S2 to be OUTSIDE of [a', b'] is obviously 1-P2=1-[(b'-a')/(b-a)]
5. Keep pulling resistors. The probability that 5 resistor will all fall OUTSIDE [a', b'] is then P={1-[(b'-a')/(b-a)]}^5 (or in general ^(N-1) where N is the number of resistors to start with.
6. Now the probability to have AT LEAST one resistor in [a', b'] is 1-{1-[(b'-a')/(b-a)]}^5
7. Repeat the above, for 2 matches out of 5, 4, 3, 2, and note all probabilities in step 6. as (P(i), i=1...5
7. We are still not done yet. Since we constraint the problem to matching the FIRST resistor extracted, and considering the problem is symmetrical for all resistors (e.g. S2 may match with S4) we need to add all these probabilities, that is P=SUM((1-P(i)), i=1...5
Plug in some numbers
a=99
b=101
b'-a'=0.1 (meaning 0.05%)
P2=0.05
1-P2=0.95
P(5)=0.95^5=0.77
P(4)=0.95^4=0.82
P(3)=0.95^3=0.86
P(2)=0.95^2=0.90
P(1)=0.95^1=0.95
SUM(1-P(i)) i=1...5=0.23+0.18+0.14+0.10+0.05 = 0.70
So the probability to find 2 resistors matched to 0.05% in 6 resistors of 1% is 70%. Of course, this result assumed an uniform distribution of the six resistor values, which may not be true. Practically, any distribution beyond uniform increases the success probability, so 93% is kind of worst case. Not sure why your simulation rendered more pessimistic results.
Repeat for 2 matches to 0.01% out of 10 resistors gives:
a=99
b=101
b'-a'=0.02 (meaning 0.01%)
P2=0.01
1-P2=0.99
P(9)=0.99^9=0.914
P(8)=0.99^8=0.923
P(7)=0.99^7=0.932
P(6)=0.99^6=0.941
P(5)=0.99^5=0.951
P(4)=0.99^4=0.961
P(3)=0.99^3=0.970
P(2)=0.99^2=0.980
P(1)=0.99^1=0.990
SUM(1-P(i)) i=1...9 = 0.01+0.02+0.03+0.039+0.049+0.059+0.068+0.077+0.086=0.438
So the probability to find 2 resistors matched to 0.01% in 10 resistors of 1% is 43.6%,
Given the prices of 0.01% resistors like Stackpole that costs $3 a pop, and the prices of 10 resistors 1% like Stackpole total cost of $1.4, I'm not convinced it is worth sorting, at least at this level of 0.01%
1. Pull a resistor out of 6 (so 5 left). Since the probability in the [a, b] interval is uniform, any value is possible there. Let's call this value S1 (sample 1).
2. Around S1, consider an interval [a', b'] defined by the desired matching tolerance.
3. Pull another resistor with value S2 (4 left). S2 can also be anywhere in [a, b] with equal probability; the probability to fall in [a', b'] is P2=(b'-a')/(b-a).
4. The probability for S2 to be OUTSIDE of [a', b'] is obviously 1-P2=1-[(b'-a')/(b-a)]
5. Keep pulling resistors. The probability that 5 resistor will all fall OUTSIDE [a', b'] is then P={1-[(b'-a')/(b-a)]}^5 (or in general ^(N-1) where N is the number of resistors to start with.
6. Now the probability to have AT LEAST one resistor in [a', b'] is 1-{1-[(b'-a')/(b-a)]}^5
7. Repeat the above, for 2 matches out of 5, 4, 3, 2, and note all probabilities in step 6. as (P(i), i=1...5
7. We are still not done yet. Since we constraint the problem to matching the FIRST resistor extracted, and considering the problem is symmetrical for all resistors (e.g. S2 may match with S4) we need to add all these probabilities, that is P=SUM((1-P(i)), i=1...5
Plug in some numbers
a=99
b=101
b'-a'=0.1 (meaning 0.05%)
P2=0.05
1-P2=0.95
P(5)=0.95^5=0.77
P(4)=0.95^4=0.82
P(3)=0.95^3=0.86
P(2)=0.95^2=0.90
P(1)=0.95^1=0.95
SUM(1-P(i)) i=1...5=0.23+0.18+0.14+0.10+0.05 = 0.70
So the probability to find 2 resistors matched to 0.05% in 6 resistors of 1% is 70%. Of course, this result assumed an uniform distribution of the six resistor values, which may not be true. Practically, any distribution beyond uniform increases the success probability, so 93% is kind of worst case. Not sure why your simulation rendered more pessimistic results.
Repeat for 2 matches to 0.01% out of 10 resistors gives:
a=99
b=101
b'-a'=0.02 (meaning 0.01%)
P2=0.01
1-P2=0.99
P(9)=0.99^9=0.914
P(8)=0.99^8=0.923
P(7)=0.99^7=0.932
P(6)=0.99^6=0.941
P(5)=0.99^5=0.951
P(4)=0.99^4=0.961
P(3)=0.99^3=0.970
P(2)=0.99^2=0.980
P(1)=0.99^1=0.990
SUM(1-P(i)) i=1...9 = 0.01+0.02+0.03+0.039+0.049+0.059+0.068+0.077+0.086=0.438
So the probability to find 2 resistors matched to 0.01% in 10 resistors of 1% is 43.6%,
Given the prices of 0.01% resistors like Stackpole that costs $3 a pop, and the prices of 10 resistors 1% like Stackpole total cost of $1.4, I'm not convinced it is worth sorting, at least at this level of 0.01%
Last edited:
10 1% "like" Stackpole: 55 cents. ROHM Semicon | ROHM Semicon ESR18EZPF1000 | Chip Resistor - Surface Mount - LCSC.COM
I took the lowest price resistors from the same manuacturer, in stock at the same distributor, since the price ratio matters. The same Rohm 10 resistors cost $1.82 at DigiKey. OTOH, Rohm doesn't do any 0.01% thin film.
But even so, 0.01% sorting (which is 10milliohm/100ohm) requires a 5 1/2 digit ohmmeter and Kelvin probes, plus the work. Myself, I'd rather buy two 0.01% resistor rather than going through the sorting process with 44% chances to succeed or 56% chances to fail, and start over. The series converges rather slow, I can calculate how large the 1% sample size for a certain probability of success (say 90%), I would expect something like 30pcs or more.
For 0.1%, a 4 1/2 multimeter is good enough, and chances to get a 0.1% pair out of 6pcs of 1% are 70%, that looks feasible, but then 0.1% resistors from Stackpole are $0.81 a pop, so compared to the cost of 6 x 1% is a flush.
Not worth the trouble IMO, unless one cannot find the needed resistors in 0.01% or 0.1% tolerances in stock, anywhere (which is very possible today).
But even so, 0.01% sorting (which is 10milliohm/100ohm) requires a 5 1/2 digit ohmmeter and Kelvin probes, plus the work. Myself, I'd rather buy two 0.01% resistor rather than going through the sorting process with 44% chances to succeed or 56% chances to fail, and start over. The series converges rather slow, I can calculate how large the 1% sample size for a certain probability of success (say 90%), I would expect something like 30pcs or more.
For 0.1%, a 4 1/2 multimeter is good enough, and chances to get a 0.1% pair out of 6pcs of 1% are 70%, that looks feasible, but then 0.1% resistors from Stackpole are $0.81 a pop, so compared to the cost of 6 x 1% is a flush.
Not worth the trouble IMO, unless one cannot find the needed resistors in 0.01% or 0.1% tolerances in stock, anywhere (which is very possible today).
Last edited:
The is an assumption that all resistors enter your possession pre-sort using the same process thus share the same probabilities. For example those bought through eBay may not share the same sample tolerances (even if 1%) due to fake/preselection and resorting. So I would place a constraint that all resistors are purchased through the the larger resellers.
^^^^
This.
I'm pretty sure when I first bought parts and didn't know any better, I'd say instead of 1% metal film they were carbon. Or they were just an older style. Still, they work as described. Within 1% of the stated value and they handle their 1/2W rating.
This.
I'm pretty sure when I first bought parts and didn't know any better, I'd say instead of 1% metal film they were carbon. Or they were just an older style. Still, they work as described. Within 1% of the stated value and they handle their 1/2W rating.
If one cannot tell metal film from carbon when ordering, then chances are high he also doesn't have an at least 4 1/2 DVM, doesn't understand tolerances in general, and doesn't need 0.1% resistors in particular, to start with.
Benb,
https://www.atecorp.com/atecorp/media/pdfs/data-sheets/genrad-1658_manual.pdf
Used and working at most a few hundred dollars.
Nice design, allows 4 terminal connection and under 10 seconds per test.
I also have one like what you used. Had a fellow in a court case claim he had measured loudspeaker lines in a stadium with one. Turns out you can’t use one to measure loudspeaker impedance! (Loudspeakers are transducers and any wind or noise will not allow you to settle in on a value.)
https://www.atecorp.com/atecorp/media/pdfs/data-sheets/genrad-1658_manual.pdf
Used and working at most a few hundred dollars.
Nice design, allows 4 terminal connection and under 10 seconds per test.
I also have one like what you used. Had a fellow in a court case claim he had measured loudspeaker lines in a stadium with one. Turns out you can’t use one to measure loudspeaker impedance! (Loudspeakers are transducers and any wind or noise will not allow you to settle in on a value.)
Last edited:
The ad said MF. They look like MF. They perform like CF.
Nothing to do at all with a meter (how do you test it before you purchase?) or being able to read a damned ad.
No typical DIY people need 0.1% resistors, either. And also no need for the condescending attitude.
Here's a nice, closed form, formula:
P=1-(1-t/T)^[N(N-1)/2]
where:
t=the target tolerance in %
T=the available resistors tolerance in %
N=the number of resistors with tolerance T to sort from
P=the probability of finding at least 2 resistors within t tolerance
Example:
t=0.01%
T=1%
N=25
...
P=95%
Could also be solved for N to find the number of needed resistors to find a matched pair with a given probability. I'll let other to determine the economic feasibility of sorting resistors for a matched pair, and if it's worth the trouble.
For:
t=0.01%
T=1%
N=10
...
P=36.3%
This matches pretty well the Monte Carlo simulation of 5 million bags of ten random resistors per bag, as in https://www.diyaudio.com/forums/par...r-starting-six-1-resistors-2.html#post6846820, which gave P=36.9%
P=1-(1-t/T)^[N(N-1)/2]
where:
t=the target tolerance in %
T=the available resistors tolerance in %
N=the number of resistors with tolerance T to sort from
P=the probability of finding at least 2 resistors within t tolerance
Example:
t=0.01%
T=1%
N=25
...
P=95%
Could also be solved for N to find the number of needed resistors to find a matched pair with a given probability. I'll let other to determine the economic feasibility of sorting resistors for a matched pair, and if it's worth the trouble.
For:
t=0.01%
T=1%
N=10
...
P=36.3%
This matches pretty well the Monte Carlo simulation of 5 million bags of ten random resistors per bag, as in https://www.diyaudio.com/forums/par...r-starting-six-1-resistors-2.html#post6846820, which gave P=36.9%
Last edited:
If anyone is wondering about practical applications of these ideas, let me introduce you to the Ship Of Theseus amplifier and its interchangeable Front End cards, including "Bon Homme Richard". SOT offers seven different Front Ends, each named for a famous American ship. You can read about the complete Ship Of Theseus project (here) . Post #1 of that thread includes a large .pdf file with schematics and descriptions of all seven Front Ends (link).
The section which covers Bon Homme Richard is attached below. Notice the discussion about resistor matching; the lab methodology should look quite familiar.
_
The section which covers Bon Homme Richard is attached below. Notice the discussion about resistor matching; the lab methodology should look quite familiar.
_
