Hello
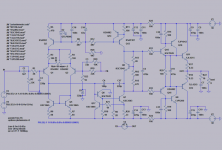
In the Doug. Self Power Amplifier book there is a 2-pole compensation VAS, as you can see in the image I've upload.
In that image you have Cp1 (100 pF) and Cp2 (1 nF) capacitors, what would be the practical resulting cdom Miller capacitance value of that VAS ?
The values of Cp1 and Cp2 capacitors are quite high, how much lower can we go for those capacitors ?
Anybody have try this type of VAS, how good it is, what is the pros and cons of this VAS ?
Thank you
Bye
Gaetan
In the Doug. Self Power Amplifier book there is a 2-pole compensation VAS, as you can see in the image I've upload.
In that image you have Cp1 (100 pF) and Cp2 (1 nF) capacitors, what would be the practical resulting cdom Miller capacitance value of that VAS ?
The values of Cp1 and Cp2 capacitors are quite high, how much lower can we go for those capacitors ?
Anybody have try this type of VAS, how good it is, what is the pros and cons of this VAS ?
Thank you
Bye
Gaetan
Attachments
Last edited:
I've not seen the two that far apart before. I simulated it though and it seems to work very well indeed. Here is what I simulated - I have even laid out a PCB for this (a compact one - for a limited size case) but have not yet got around to building it. The CFP drivers may be excessive 
Attachments
Hello jaycee
The value of C4 and C17 are relatively high, is it because it's a beta enhance vas, have you try much lower caps value ?
Quite all beta enhance vas I've seen used high value cdom capacitors, this type of vas seem prone to oscillate.
Have you calculate the resulting miller capacitance value of your 2-pole comp vas ?
Thank
Bye
Gaetan
The value of C4 and C17 are relatively high, is it because it's a beta enhance vas, have you try much lower caps value ?
Quite all beta enhance vas I've seen used high value cdom capacitors, this type of vas seem prone to oscillate.
Have you calculate the resulting miller capacitance value of your 2-pole comp vas ?
Thank
Bye
Gaetan
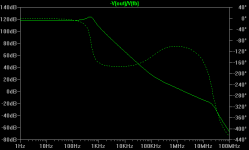
lower values caused oscillation. You'll see also the R-C network in the feedback path, this was also needed. I plotted the loop gain. There is a peak at 500KHz but this doesn't seem to cause a problem. The 0dB point is at about 1.9MHz with a phase of -104 degrees.
In simulation I've thrown square waves and sines at it, and it seems stable. It's also stable into a 1u capacitor, although it needs an L-R parallel network on the output for that.
I think 5th element tried a similar circuit here too, with good results.
In simulation I've thrown square waves and sines at it, and it seems stable. It's also stable into a 1u capacitor, although it needs an L-R parallel network on the output for that.
I think 5th element tried a similar circuit here too, with good results.
Attachments
Yes he did. Take a look at this thread:
http://www.diyaudio.com/forums/solid-state/160061-slones-11-4-blameless-2.html#post2063936
http://www.diyaudio.com/forums/solid-state/160061-slones-11-4-blameless-2.html#post2063936
Cp2 value seems uselessly high...
Cp1 value is also high considering that this is a single
transistor VAS that is compensated.
Such a high value would make sense with an enhanced
VAS which would add an common collector bjt to drive
it, as in the blameless.
Typical values would be 100 and 330 pF for an enhanced vas,
56 and 180 pF for a single bjt vas;
Of course, these values are to be adjusted according to the first
stage current capabilities.
To answer your question, although a high value miller cap slow down
an amp, with TPC , its influence is reduced by the resistor that act as
an attenuator, thus limiting the frequency dependent local negative
feed back, and thus extending the vas -3db frequency response..
Cp1 value is also high considering that this is a single
transistor VAS that is compensated.
Such a high value would make sense with an enhanced
VAS which would add an common collector bjt to drive
it, as in the blameless.
Typical values would be 100 and 330 pF for an enhanced vas,
56 and 180 pF for a single bjt vas;
Of course, these values are to be adjusted according to the first
stage current capabilities.
To answer your question, although a high value miller cap slow down
an amp, with TPC , its influence is reduced by the resistor that act as
an attenuator, thus limiting the frequency dependent local negative
feed back, and thus extending the vas -3db frequency response..
The way I understand it, the equivalent Cdom would be the series equivalent of 100pF and 1nF (about 90 pF).
BTW, this is extensively discussed in the Bob Cordell thread on negative feedback.
jan didden
Hello
Looking at a Andrew T formula for those two cap, it seem that we need anyway a high value cap.
http://www.diyaudio.com/forums/solid-state/160061-slones-11-4-blameless-2.html#post2064029
Anyone have check the slew rate of a amp with a 2-pole compensation VAS compared to the same amp with a standard VAS ?
I've take a look at the Bob Cordell thread on negative feedback, it's a quite long thread to read.
Wen I do amps, using a phase lead cap and a good pcb layout, I can go down to 19 pF for the cdom cap, using a 10 pF phase lead cap, I check it with a 10 khz square wave. It give fast and clean sounding amps (it still need an input section with a good linearity). But I don't use a beta enhance vas.
Thank
Bye
Gaetan
Looking at a Andrew T formula for those two cap, it seem that we need anyway a high value cap.
http://www.diyaudio.com/forums/solid-state/160061-slones-11-4-blameless-2.html#post2064029
Anyone have check the slew rate of a amp with a 2-pole compensation VAS compared to the same amp with a standard VAS ?
I've take a look at the Bob Cordell thread on negative feedback, it's a quite long thread to read.
Wen I do amps, using a phase lead cap and a good pcb layout, I can go down to 19 pF for the cdom cap, using a 10 pF phase lead cap, I check it with a 10 khz square wave. It give fast and clean sounding amps (it still need an input section with a good linearity). But I don't use a beta enhance vas.
Thank
Bye
Gaetan
Last edited:
It's not really two pole so much as pole-zero compensation. After all, a two-pole compensator would result in at least a three-pole system, which is nontrivial to solve for best results. With a zero, you can hope to position it near an existing pole, to get some cancellation and improve risetime or somesuch.
Looking at the network alone, it has the same HF behavior as a miller cap, since when Xc2 << R2, the resistor disappears and it looks like two caps in series. It cuts off somewhere before DC, since it makes a second order high pass filter. If the time constants are staggered (i.e., Cp2 working into Rp, Cp1 working into Rb), there will be some lead/lag action. Note, of course, pure RC poles can never overlap, be complex or be in the right half-plane.
When the impedances of stages in an RC filter are close, the poles get pushed apart. A buffered RC-RC filter (i.e., RC--buffer--RC) has a critically damped response, which for a lowpass is:
H = 1 / (s^2 + 2zws + w^2)
where w is the angular cutoff frequency w = 1 / RC and z is zeta, the damping factor. (The highpass equivalent is s^2 H, where you can imagine the s factors as derivatives, hence the high-pass filter's other name, the differentiator -- under certain conditions.)
For the unbuffered filter, finite values of impedance result in an overdamped system (zeta > 1). Zeta is 1.205 for the case of decade-stepped impedance, i.e. R2/C2 = 10 R1/C1, which isn't too bad, and the component values are usually pretty reasonable. Zeta rises to 3.5 for equal impedances (R1 = R2, C1 = C2), which is pretty awful. (A butterworth filter has maximally flat frequency response, with damping coefficient sqrt(2) / 2 ~= 0.7071.) This gives you some idea of the poor performance that unamplified RC networks give.
A complete analysis of this circuit would result in lots of ugly terms. This is a poor example of a feedback circuit: the input is coupled to the output, so at very high frequencies, gain is positive (near unity), while at low frequencies it's very high (roughly 1 / h_oe), and negative (i.e., inverting). You get feed-forward and feed-back relations, and everything depends on Zin and Zload.
We can make some helpful assumptions:
- Assume the input is constant current. Such a circuit is usually found after a diffamp, which has a reasonably constant-current output.
- Assume the collector output is constant current. Same justification, and the CCS shown is also going to be a collector.
- The actual load will generally be R || C, but perhaps we can make the excuse that the capacitance can be lumped into Cp2, and R will be larger than Xcp2 for the frequencies we're interested in. Alternately, we can look at the circuit alone with no load, and assume it will act slower in a real circuit.
This results in a circuit that looks like:
- Current input
- Output is a voltage controlled current source, corresponding to the transistor's transconductance (gm = dIc / dVbe = Ic / Vth)
- Network between input and output
Note I've renamed Cp1 to C1 for simplicity. Same thing.
So now we can use good old Nodal Analysis to figure it out, among other approaches.
@ Vbe:
i_in = (Vbe - V2) / (1 / (C1 s)) + Vbe / Rpi
@ V2:
(Vbe - V2) / (1 / (C1 s)) = V2 / R1 + (V2 - Vo) / (1 / (C2 s))
@ Vo:
(V2 - Vo) / (1 / (C2 s)) + i_out = i_c
And
i_c = Vbe Ic / Vth
Where Ic is the quiescent current (remember, BJTs are exponential, so i_c depends on Ic) and Vbe is the AC base voltage. In fact, all these variables (Vbe, i_c, i_in, i_out, V2, Vo) are AC quantities.
Rearranging, we get the 3x3 linear equation:
Which could be reduced to a 2x2 system since we aren't interested in V2, or 1x1 (i.e., a proper transfer function) since we want i_out.
Complete transfer function later...
Tim
Looking at the network alone, it has the same HF behavior as a miller cap, since when Xc2 << R2, the resistor disappears and it looks like two caps in series. It cuts off somewhere before DC, since it makes a second order high pass filter. If the time constants are staggered (i.e., Cp2 working into Rp, Cp1 working into Rb), there will be some lead/lag action. Note, of course, pure RC poles can never overlap, be complex or be in the right half-plane.
When the impedances of stages in an RC filter are close, the poles get pushed apart. A buffered RC-RC filter (i.e., RC--buffer--RC) has a critically damped response, which for a lowpass is:
H = 1 / (s^2 + 2zws + w^2)
where w is the angular cutoff frequency w = 1 / RC and z is zeta, the damping factor. (The highpass equivalent is s^2 H, where you can imagine the s factors as derivatives, hence the high-pass filter's other name, the differentiator -- under certain conditions.)
For the unbuffered filter, finite values of impedance result in an overdamped system (zeta > 1). Zeta is 1.205 for the case of decade-stepped impedance, i.e. R2/C2 = 10 R1/C1, which isn't too bad, and the component values are usually pretty reasonable. Zeta rises to 3.5 for equal impedances (R1 = R2, C1 = C2), which is pretty awful. (A butterworth filter has maximally flat frequency response, with damping coefficient sqrt(2) / 2 ~= 0.7071.) This gives you some idea of the poor performance that unamplified RC networks give.
A complete analysis of this circuit would result in lots of ugly terms. This is a poor example of a feedback circuit: the input is coupled to the output, so at very high frequencies, gain is positive (near unity), while at low frequencies it's very high (roughly 1 / h_oe), and negative (i.e., inverting). You get feed-forward and feed-back relations, and everything depends on Zin and Zload.
We can make some helpful assumptions:
- Assume the input is constant current. Such a circuit is usually found after a diffamp, which has a reasonably constant-current output.
- Assume the collector output is constant current. Same justification, and the CCS shown is also going to be a collector.
- The actual load will generally be R || C, but perhaps we can make the excuse that the capacitance can be lumped into Cp2, and R will be larger than Xcp2 for the frequencies we're interested in. Alternately, we can look at the circuit alone with no load, and assume it will act slower in a real circuit.
This results in a circuit that looks like:
- Current input
- Output is a voltage controlled current source, corresponding to the transistor's transconductance (gm = dIc / dVbe = Ic / Vth)
- Network between input and output
An externally hosted image should be here but it was not working when we last tested it.
Note I've renamed Cp1 to C1 for simplicity. Same thing.
So now we can use good old Nodal Analysis to figure it out, among other approaches.
@ Vbe:
i_in = (Vbe - V2) / (1 / (C1 s)) + Vbe / Rpi
@ V2:
(Vbe - V2) / (1 / (C1 s)) = V2 / R1 + (V2 - Vo) / (1 / (C2 s))
@ Vo:
(V2 - Vo) / (1 / (C2 s)) + i_out = i_c
And
i_c = Vbe Ic / Vth
Where Ic is the quiescent current (remember, BJTs are exponential, so i_c depends on Ic) and Vbe is the AC base voltage. In fact, all these variables (Vbe, i_c, i_in, i_out, V2, Vo) are AC quantities.
Rearranging, we get the 3x3 linear equation:
Code:
[ C1 s + 1 / Rpi , -C1 s , 0 ] [ i_in ]
A = [ C1 s , -(C2 + C2) s - 1 / R1 , C2 s ] = [ 0 ]
[ -Ic/Vth , C2 s , C2 s ] [ -i_out ]Complete transfer function later...
Tim
- Status
- This old topic is closed. If you want to reopen this topic, contact a moderator using the "Report Post" button.