Hello All,
I am trying to calculate the resulting sound pressure levels (SPL) from two different voltages applied to a speaker (not at the same time). The speaker is 4 ohms with a sensitivity of 86 dB, for 2.83V.
For example: If the voltage difference was 0.5 Vrms, the calculation would be 0.5 x (86 / 2.83) = 15.2 dB SPL. Which I interpret to mean that the higher voltage produces a sound about twice as loud as the lower voltage.
Correct?
Cheers,
ceulrich
I am trying to calculate the resulting sound pressure levels (SPL) from two different voltages applied to a speaker (not at the same time). The speaker is 4 ohms with a sensitivity of 86 dB, for 2.83V.
For example: If the voltage difference was 0.5 Vrms, the calculation would be 0.5 x (86 / 2.83) = 15.2 dB SPL. Which I interpret to mean that the higher voltage produces a sound about twice as loud as the lower voltage.
Correct?
Cheers,
ceulrich
AnnenB, thanks for the reply. I understand that a voltage difference of 0.5 is a difference of -6dB, but how do I convert that difference to a sound pressure level?
Cheers,
ceulrich
Cheers,
ceulrich
Yes, of course, I was using the sensitivity value like a linear calibration factor, which it is not. If I convert the individual voltages to SPLs, then take the difference I get the expected 6dB SPL for a voltage difference of 0.5.
Thanks for helping me get my head screwed on straight.
Cheers,
ceulrich
Thanks for helping me get my head screwed on straight.
Cheers,
ceulrich
Hi,
Db have been invented to have a meaningful way to compare ratio level between different fields: electronic, acoustic, digital...
When used without anything with them ( eg: db ) this is what happen.
Once you have something added to them things change and they are now referenced to something:
DbFS : used in digital and Full Scale refer to the absolute maximum level digital can produce ( =0dbfs, iow in digital you'll often see -xx dbfs ( minus xx dbfs)
DbSPL: acoustic level referenced to 1Pa which equal to 94dbSPL
DbU: in electronic, voltage related to 0.7746 Volts ( without relation to any given impedance)
Etc,etc,etc,...
When talking about Voltage the logarithmic scale is based on 20log.
Eg 20log(2)= 6.
Iow +6db equal doubling voltage.
When talking about power then its based on 10log.
Eg 10log(2)= 3.
Iow when you double power ( of an amp) you gain +3db.
So to answer your initial question: 2,83v into 4ohm load gives 86db ( @ 1meter)
How much power do you send to your loudspeaker to have 86db?
You need an Ohm's law wheel to the rescue if like myself you can't remember the variations around Ohm's law( i'll let you google it 😉 ).
We know to define power from known Voltage and Resistance ( impedance), Power= (V)2/R - V squared, divided by R
So (2,83)2 / 4 = 2
2w.
Now we add our 0,5v to 2,83v it gives ( 3,33)2 /4 = 2,77w
2,77/2= 1.35 ratio.
As we are talking power we'll use 10log:
10log(1,35)= 1.3db
86+1,3= 87,3db for 2,77 watts (3,33V into 4 ohms).
Db have been invented to have a meaningful way to compare ratio level between different fields: electronic, acoustic, digital...
When used without anything with them ( eg: db ) this is what happen.
Once you have something added to them things change and they are now referenced to something:
DbFS : used in digital and Full Scale refer to the absolute maximum level digital can produce ( =0dbfs, iow in digital you'll often see -xx dbfs ( minus xx dbfs)
DbSPL: acoustic level referenced to 1Pa which equal to 94dbSPL
DbU: in electronic, voltage related to 0.7746 Volts ( without relation to any given impedance)
Etc,etc,etc,...
When talking about Voltage the logarithmic scale is based on 20log.
Eg 20log(2)= 6.
Iow +6db equal doubling voltage.
When talking about power then its based on 10log.
Eg 10log(2)= 3.
Iow when you double power ( of an amp) you gain +3db.
So to answer your initial question: 2,83v into 4ohm load gives 86db ( @ 1meter)
How much power do you send to your loudspeaker to have 86db?
You need an Ohm's law wheel to the rescue if like myself you can't remember the variations around Ohm's law( i'll let you google it 😉 ).
We know to define power from known Voltage and Resistance ( impedance), Power= (V)2/R - V squared, divided by R
So (2,83)2 / 4 = 2
2w.
Now we add our 0,5v to 2,83v it gives ( 3,33)2 /4 = 2,77w
2,77/2= 1.35 ratio.
As we are talking power we'll use 10log:
10log(1,35)= 1.3db
86+1,3= 87,3db for 2,77 watts (3,33V into 4 ohms).
Last edited:
Hi, here's a good calculator for comparing two voltages http://www.sengpielaudio.com/calculatorVoltagePower.htmHello All,
I am trying to calculate the resulting sound pressure levels (SPL) from two different voltages applied to a speaker (not at the same time). The speaker is 4 ohms with a sensitivity of 86 dB, for 2.83V.
For example: If the voltage difference was 0.5 Vrms, the calculation would be 0.5 x (86 / 2.83) = 15.2 dB SPL. Which I interpret to mean that the higher voltage produces a sound about twice as loud as the lower voltage.
Correct?
Cheers,
ceulrich
Note impedance is immaterial (assumes it's held constant).
If in your example you meant the voltage difference was 0.5V such that the voltage of comparison is either 3.33V or 2.33V, depending on direction
then the dB gain or loss is either +1.4dB or -1.7 like shown.
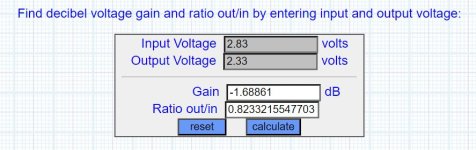
If you meant the compared voltage was actually 0.5V, then you get this, about -15dB.
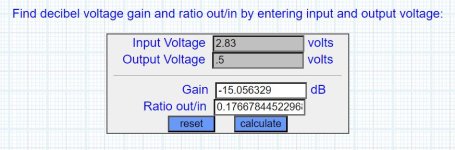
Those dB differences will be the same dB differences in SPL measurements of speaker output.
The world generally equates a 10dB difference as a doubling of perceived sound volume.
This notion however, is an assessment of the average of subjective judgment calls....and made long ago.....
Personally, I think 10dB is much more than doubling. I perceive 6dB as doubling,
You should judge for yourself 🙂
Hope this helped...
Hello krivium, thanks for the detailed explanation. I followed your logic and calculations perfectly.
Hello mark100, thanks for those links, and your comments. Your point about the question of an absolute or differential measurement is well taken. In my original post, I was thinking about a differential measurement. Your observation that the resulting calculated value depends on which side of 2.83 one is considering, is again, well taken. These different scenarios’ have added to my confusion in the past few days, and convinced me to think carefully when making the calculations. I agree, 10dB is very generous.
Cheers,
ceulrich
Hello mark100, thanks for those links, and your comments. Your point about the question of an absolute or differential measurement is well taken. In my original post, I was thinking about a differential measurement. Your observation that the resulting calculated value depends on which side of 2.83 one is considering, is again, well taken. These different scenarios’ have added to my confusion in the past few days, and convinced me to think carefully when making the calculations. I agree, 10dB is very generous.
Cheers,
ceulrich
- Home
- Loudspeakers
- Full Range
- Question About SPL Calculations