In a >=2nd order sigma-delta amp, where do the extra lowpass sections go? I assume in the feedback loop and not in between the first integrator and the comparator. And how does one choose the corner frequencies for each extra lowpass/integrator?
Sorry for the newbish question, and thanks in advance for tolerating it.
Tim
Sorry for the newbish question, and thanks in advance for tolerating it.
Tim
All integrators usually have the same time-constant, but the difference lies in the different gains when they are summed.
What loop order are you looking at ?
Regards
Charles
True, I wasn't thinking there. Though I seem to remember seeing amps with a lowpass instead of an integrator in the feedback loop. How does one choose the unity gain frequencies in the integrators? Assuming that is the best way to describe an integrator's response.
I'm not planning on any class D amps right now, in the future I'll probably build something 2nd order, but for now I just want a greater understanding of the topology.
If you know of any websites or readily available books that would give me some introductory loop theory (beyond gain vs bandwidth and the sort) that would be helpful.
Normally the forward path of the loop is a chain of integrators. Lowpass filters can be used, but normally you'll only find this in cases when the loop is constructed using passive components (mostly passive controlled self-oscillating class D amps) or when the designer intentionally wanted to limit loop gain at lower frequencies (e.g. UcD).
The traditional method for synthesising a deltasigma loop is thus:
1) One takes a chain of n integrators. Go easy on your math skills and start with a time constant of unity. This realises a loop function 1/s^n. This loop function is obviously not going to make a stable loop.
2) To make the loop stable, the transfer function must fold over from an nth order function to a 1st order at some frequency before the unity gain point. The loop gain looks like a steep downward slope of -n*20dB/dec, changing to a less steep slope of 20dB/dec shortly before the unity gain point. It is common to make this crossover using a butterworth function. This means that to the loop function a set of n-1 zeros is added distributed evenly along a circle of radius Wchangeover.
3) The zeros are practically realised by making a weighted sum across all integrator outputs. The loop function is of the form
(a1+a2*s+a3*s^2+ ... +an*s^(n-1))/s^n. Symbolically or numerically determine a[n] to get the zeros where you wanted them.
4) scale the whole function by a constant such as to get the unity point somewhere in the 1st order region as planned. Individual internal gains can be scaled (with retention of overall gain of course!) to optimise signal swings.
4) becomes moot when the circuit is a 1-bit converter. Gain will be determined automatically by the probability density function of the noise that comes out of the loop.
When you're designing a PWM system, usually the equation runs backward. First you set the switching frequency, from this follows the unity gain point, and from this the changeover frequency.
When you're designing a 1-bit converter, the choice of changeover frequency determines the maximum stable modulation index.
My own method produces somewhat more optimal coefficient sets, and works equally well with loop functions with complex poles (and can be used to include output filters), but is quite complicated to explain here.
The traditional method for synthesising a deltasigma loop is thus:
1) One takes a chain of n integrators. Go easy on your math skills and start with a time constant of unity. This realises a loop function 1/s^n. This loop function is obviously not going to make a stable loop.
2) To make the loop stable, the transfer function must fold over from an nth order function to a 1st order at some frequency before the unity gain point. The loop gain looks like a steep downward slope of -n*20dB/dec, changing to a less steep slope of 20dB/dec shortly before the unity gain point. It is common to make this crossover using a butterworth function. This means that to the loop function a set of n-1 zeros is added distributed evenly along a circle of radius Wchangeover.
3) The zeros are practically realised by making a weighted sum across all integrator outputs. The loop function is of the form
(a1+a2*s+a3*s^2+ ... +an*s^(n-1))/s^n. Symbolically or numerically determine a[n] to get the zeros where you wanted them.
4) scale the whole function by a constant such as to get the unity point somewhere in the 1st order region as planned. Individual internal gains can be scaled (with retention of overall gain of course!) to optimise signal swings.
4) becomes moot when the circuit is a 1-bit converter. Gain will be determined automatically by the probability density function of the noise that comes out of the loop.
When you're designing a PWM system, usually the equation runs backward. First you set the switching frequency, from this follows the unity gain point, and from this the changeover frequency.
When you're designing a 1-bit converter, the choice of changeover frequency determines the maximum stable modulation index.
My own method produces somewhat more optimal coefficient sets, and works equally well with loop functions with complex poles (and can be used to include output filters), but is quite complicated to explain here.
I once derived the maths to determine the coefficients for a given NTF for loop-orders up to five. I know that some programs can do this easily but I don't own one.
It is difficult to determine the cutuff frequency and order of an optimal NTF however but the calculation of the coefficients for a given NTF is trivial.
Something that isn't trivial (at least to my knowledge) is the determination of optimal integrator clipping levels for 1-bit modulators.
If someone is interested I can post my findings here.
Regards
Charles
It is difficult to determine the cutuff frequency and order of an optimal NTF however but the calculation of the coefficients for a given NTF is trivial.
Something that isn't trivial (at least to my knowledge) is the determination of optimal integrator clipping levels for 1-bit modulators.
If someone is interested I can post my findings here.
Regards
Charles
Bruno, when you talk about PWM I assume you talk about clock based amps. In that case, as you suggest, you determinte the sw. freq. and then the 0dB point.
I suppose you are trying to say that the 0dB point in the open loop function must be placed at <Fs/2, right?
Thanks
I suppose you are trying to say that the 0dB point in the open loop function must be placed at <Fs/2, right?
Thanks
A similar reasoning goes for self-oscillating amps, whereby self-oscillation is produced using hysteresis or a second turnover point at a higher frequency, transitioning to 3rd order rolloff (or 2nd order + prop delay).Pierre said:
Yes. In practice, you will find you'll need to go even further down to Fs/3.Pierre said:
I don't know if higher order self-oscillating sigma-delta will work. If the whole thing is a system is a 2nd order integrator for example, there will be a phase shift of 180° at all frequencies above unity gain, so the whole thing can oscillate at any frequency (and will do so).
Also adding zeros will not change that for frequencies below the zero frequencies, so the oscillation frequency will just be kept below the frequencies of the zeros.
In my opinion, self oscillating converters will only work as a system of order 1.
digi
Also adding zeros will not change that for frequencies below the zero frequencies, so the oscillation frequency will just be kept below the frequencies of the zeros.
In my opinion, self oscillating converters will only work as a system of order 1.
digi
Not so. When you add a zero, phase shift below this frequency will converge asymptotically to 180 degrees. Above this frequency, phase shift will converge asymptotically to 90 degrees. In this state, the modulator will not oscillate at all. You will have to add delays or real poles at frequencies beyond the location of the zero to effect oscillation. In a sampled system, the delay is automatically present, in the form of one sample delay.digitoxin said:
Yes, thats true. But my argument not about getting it to oscillate at some frequency (you can always throw in some poles), but that it is not possible to get oscillation out of the audio band in a real second order system.
I will refine my argument as such: The better noise suppression from a higher order sigma delta is because of the increased gain in the audio band. In the case 40db/dec is reached (against the 20db/dec of a first order system), the phase shift will be enough to start it oscillating. If it is lower (due to some pole/zero arragment and you are on the save side, there is hardly more gain compared to a straight first order system).
So, you might end up like something that looks like its second order, but in reality has not much more gain compared to a first order system (and will also have noise figures like a first order system)
For example: Real integrator (pole at zero freqency) + zero a little above the audio band: The phase shift at lower frequencies (nearly 180°) + a little delay (even jsut 100ns) will be enough to make it oscillate in the audio band, also the zero takes away some gain and makes it more like a first order system
Or a clever pole/zero arragment that will make a phase shift of 120° + a ripple around that value will also not work, because a ripple in the frequency domain is a delay in the time domain -> very bad.
On another note: I looked at the Ucd patent and i don't like what i see there.
Unless something has been done about this i see a great problem:
If a load is connected, everything is fine. But if there is no load present, the Q of the output filter will get very high, causing a huge phase shift at the pole frequencies and bring down the oscillation frequency. So, there will be a quite high output voltage and high reactive energy transfer in a no load no input condition, which is not nice at least. Especially in high power amps output voltages can be dangerously high when you don't expect anything on the output. Of course this only applies to real amps not active systems with a direct connection to the loudspeaker.
digi
Now look here. I'm entirely happy to explain people how things work. I'm all for spreading knowledge. However, some folks go into the offensive to impress their own misunderstandings upon me. Sorry, if you can't ask questions, I'm not giving answers. I can only tell you your analysis is quite mistaken on both counts. Come back when you know how to ask questions instead of telling me that I'm wrong and that I'm missing things here and there.
If you believe your own version to be correct, well you can have it. There you go.
If you believe your own version to be correct, well you can have it. There you go.
I don't want to impress anyone or wanted to be offensive. I have just posted my opinion, if i am wrong, i am happy to be corrected. I don't say that i am the owner of the only truth, what i posted is just what i notices based on my observations. I did some calculations regarding the Ucd thing and thats what came out, open for discussion.
digi
digi
Cool, let's have a look.
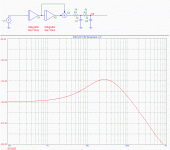
1a) 2nd order self-oscillating deltasigma.
See attached drawing. The modulator has two poles at DC, one real zero before the intended switching frequency, two real poles after it.
Now look at the phase plot. As close as the phase shift gets to 180 degrees at low frequencies, it never gets there. It has only one crossover point at 180 degrees (here 133kHz). This is expressed as "second order loops are unconditionally stable". After an overload, the loop will always return to stable oscillation at the one and only crossover point.
1b higher order deltasigma modulators.
These modulators /do/ cross 180º at a lower frequency. Therefore, the modulator has two potential oscillation frequencies. However, for stable oscillation to persist, not only must the phase shift be 180º, also the loop gain must be unity. In this case, the "gain" is large signal gain. As you are undoubtedly aware, gain of two-level systems is inversely proportional to the amplitude of the oscillation as seen at the comparator inputs.
When the modulator starts up first, oscillation will start at the intended frequency. Once that is established, and because the attenuation of the two integrators is large at this frequency, loop gain is large. At the lower 180º point, therefore, gain is much higher than 1 and the system will be stable.
Now, when the modulator is overloaded (clipped) large signal gain becomes low, because the amplitude at the comparator is high. The integrators run away and instantly, gain is so low that the lower oscillation frequency becomes viable.
So, deltasigma modulators of order >2 start up stable, but are not unconditionally stable. They can shift to "unwanted" modes after an overload.
The problem is usually addressed by clipping the integrators, thus increasing system gain, preventing stable oscillation at the lower crossover frequencies. In this way, it's quite easy to build high-order systems that come back stably after overloads. I'm doing this as a matter of fact in discrete A/D circuits, where I usually employ 6th or 7th order modulators.
1a) 2nd order self-oscillating deltasigma.
See attached drawing. The modulator has two poles at DC, one real zero before the intended switching frequency, two real poles after it.
Now look at the phase plot. As close as the phase shift gets to 180 degrees at low frequencies, it never gets there. It has only one crossover point at 180 degrees (here 133kHz). This is expressed as "second order loops are unconditionally stable". After an overload, the loop will always return to stable oscillation at the one and only crossover point.
1b higher order deltasigma modulators.
These modulators /do/ cross 180º at a lower frequency. Therefore, the modulator has two potential oscillation frequencies. However, for stable oscillation to persist, not only must the phase shift be 180º, also the loop gain must be unity. In this case, the "gain" is large signal gain. As you are undoubtedly aware, gain of two-level systems is inversely proportional to the amplitude of the oscillation as seen at the comparator inputs.
When the modulator starts up first, oscillation will start at the intended frequency. Once that is established, and because the attenuation of the two integrators is large at this frequency, loop gain is large. At the lower 180º point, therefore, gain is much higher than 1 and the system will be stable.
Now, when the modulator is overloaded (clipped) large signal gain becomes low, because the amplitude at the comparator is high. The integrators run away and instantly, gain is so low that the lower oscillation frequency becomes viable.
So, deltasigma modulators of order >2 start up stable, but are not unconditionally stable. They can shift to "unwanted" modes after an overload.
The problem is usually addressed by clipping the integrators, thus increasing system gain, preventing stable oscillation at the lower crossover frequencies. In this way, it's quite easy to build high-order systems that come back stably after overloads. I'm doing this as a matter of fact in discrete A/D circuits, where I usually employ 6th or 7th order modulators.
Attachments
Second post because I haven't found out yet how to attach more than one file to one post.
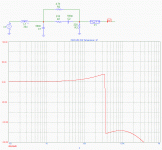
2) UcD. Attached is the circuit and phase plot of the version known from the patent. I've purposefully left the output open, so you get the situation you were "worrying" (I doubt that) about.
As you can see, the phase lead network simply keeps the phase response above the 180º line. There is only one 180º crossover, which is exactly where I wanted it to be.
2) UcD. Attached is the circuit and phase plot of the version known from the patent. I've purposefully left the output open, so you get the situation you were "worrying" (I doubt that) about.
As you can see, the phase lead network simply keeps the phase response above the 180º line. There is only one 180º crossover, which is exactly where I wanted it to be.
Attachments
phase_accurate said:
Unfortunately, yes. At least in time quantised systems. As far as the actual signals are concerned, time-quantised deltasigma is a chaotic system elusive to modelling other than full-blown time simulation (or a practical execution).
When you're not working with time-quantised systems, you can indeed derive signal levels mathematically and set the clip levels thus.
According to some analyses (see James Angus, The Effect of Noise Transfer Function Shape on Idle Tones in Sigma-Delta Modulators, AES ppt 6450), yes.Kenshin said:
What you find in practice when you make a plot of the 1st integrator output, you get a noisy "sawtooth" of which the frequency is dependent of the DC input (and equal to |fs*M|). What James found was that different choices of NTF (complex zeros or not) had a greater effect on the presence of these tones in the audio band than the mere difference in loop gain alone. I can't get my head around it yet, empirically, but there's no getting round his results.
- Status
- Not open for further replies.