I agreed up until the last sentence. The real problem is the design was bad (I am specifically referring to early class B transistor designs). Feedback cannot make those good because time is involved.
Ed
And why refer to... early Class B transistor amps... in a tube (mostly HI-FI) forum, thread? You posted a blunt opinion without full context. Kind of Twitterish...?
It's a reactive device. First it stores energy then releases it after excitation ceases, or the vacuum tube turns off. Both cycles constitute part of the audio signal. Again, not claiming it results in discreet stair-step FB error correction but a lot of the insistence on instantaneous action has me wondering if the rate of change of phase isn't group delay.
Spend an afternoon with LTSpice and schematics from legacy commercial products from the tube era. It's not difficult to find examples with front end error amps exhibiting unacceptable levels of uncorrected distortion that were 'fixed' by adding gain and fb.
No, he is right. If you use little or moderate amounts of nfb on a not very linear amp, the results get worse.
The lower harmonics do decrease but the higher harmonics will rise. It sounds worse rather than better.
You can only afford moderate or low nfb when you have a very linear amp to begin with.
Otherwise, use lots of nfb to get beyond the point where the higher harmonics also decrease.
Tube amps generally do not allow high nfb levels due to the phase shift in an output xformer, so only moderate amounts were possible.
As a consequence, tube amps with moderate nfb sounded not very nice and nfb got the blame.
Jan
The lower harmonics do decrease but the higher harmonics will rise. It sounds worse rather than better.
You can only afford moderate or low nfb when you have a very linear amp to begin with.
Otherwise, use lots of nfb to get beyond the point where the higher harmonics also decrease.
Tube amps generally do not allow high nfb levels due to the phase shift in an output xformer, so only moderate amounts were possible.
As a consequence, tube amps with moderate nfb sounded not very nice and nfb got the blame.
Jan
High, moderate... you say only moderate works, but moderate sounds bad. This is another example of short clip, twitterish, forum-speak. You have to use what works for the design and no more. Or just start over if the amp sucks. Plenty of cheap FB amps sound awsome. They use what they need.
As far as I could trace it back, bad press for negative-feedback amplifiers started with a 1966 article with a mistake in it, see http://linearaudio.net/sites/linearaudio.net/files/volume1ltemvdg.pdf
Try to read what I wrote, it's not what you say.
See if you can understand the attached.
Ask me if you don't; I'll be happy to explain.
Jan
Attachments
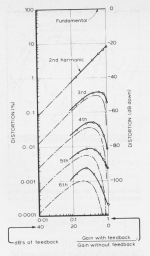
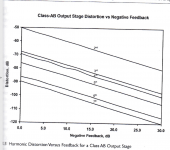
You have posted two conflicting curve sets. The 1st includes re-entrant distortion and the 2nd set does not. Both leave out important information such as amplitude versus amplifier capability and bias level, and frequency of the signal versus the amplifier BW.
The signal amplitude is quite important for the class AB case, since the crossover distortion is occurring in a very small amplitude window around zero.
The Baxandall case appears to show some actual data measurements with the dotted lines. Which are diverging more from the apparently calculated curves with higher harmonics. This would be expected with a slightly off phase compensation, due to the increasing distortion re-circulation required for generation of the higher harmonics. The usual phase compensation cap for the N Fdbk is not likely to work perfectly over the full amplifier bandwidth.
The signal amplitude is quite important for the class AB case, since the crossover distortion is occurring in a very small amplitude window around zero.
The Baxandall case appears to show some actual data measurements with the dotted lines. Which are diverging more from the apparently calculated curves with higher harmonics. This would be expected with a slightly off phase compensation, due to the increasing distortion re-circulation required for generation of the higher harmonics. The usual phase compensation cap for the N Fdbk is not likely to work perfectly over the full amplifier bandwidth.
Last edited:
OK, I will try to explain.
The difference between re-entrant and not is the whole issue. They are not conflicting - they shed light on two situations, where nfb has a different effect depending on how much you apply.
The Baxandall amp is just a single ended FET stage with relatively large open loop non-linearity. When you start to introduce feedback, the low order harmonics start to drop as expected, but the higher order harmonics start to rise until they also start to decrease too, above a certain level of feedback.
The Cordell graph is from an amp that is relatively linear even open loop, and you see that as soon as you start to apply nfb, all harmonics start to decrease (although not perfectly linearly).
If you would analyze it mathematically, you would see the same.
Now, you can assimilate this and get smarter, or continue to tap dance around it because no matter what you want to find arguments, whatever bizarre, like 'slight off phase compensation' (very creative, I give you that); to counter this.
That's your loss; I'm sure there are a lot of readers here who do pick up on this. and understand the significance.
Jan
The difference between re-entrant and not is the whole issue. They are not conflicting - they shed light on two situations, where nfb has a different effect depending on how much you apply.
The Baxandall amp is just a single ended FET stage with relatively large open loop non-linearity. When you start to introduce feedback, the low order harmonics start to drop as expected, but the higher order harmonics start to rise until they also start to decrease too, above a certain level of feedback.
The Cordell graph is from an amp that is relatively linear even open loop, and you see that as soon as you start to apply nfb, all harmonics start to decrease (although not perfectly linearly).
If you would analyze it mathematically, you would see the same.
Now, you can assimilate this and get smarter, or continue to tap dance around it because no matter what you want to find arguments, whatever bizarre, like 'slight off phase compensation' (very creative, I give you that); to counter this.
That's your loss; I'm sure there are a lot of readers here who do pick up on this. and understand the significance.
Jan
That's exactly what I said back in post #74
As far as violating physics, you are the one assuming instantaneous transmission around the loop, not me. But after a nSec or so, it does not matter anyway unless you have a GHz+ scope to see it..
As far as tube amps being unable to fix distortion due to the limited BW OT, I have mentioned the easy fix several times. Either use some "local" N Fdbk around the distorting output tube stage or make the global N Fdbk transition to "local" Fdbk (removing the OT from the loop) at some HF. Not that hard. Dynaco did it.
As far as violating physics, you are the one assuming instantaneous transmission around the loop, not me. But after a nSec or so, it does not matter anyway unless you have a GHz+ scope to see it..
As far as tube amps being unable to fix distortion due to the limited BW OT, I have mentioned the easy fix several times. Either use some "local" N Fdbk around the distorting output tube stage or make the global N Fdbk transition to "local" Fdbk (removing the OT from the loop) at some HF. Not that hard. Dynaco did it.
Last edited:
The ‘feedback is bad’ thing really got wings after the Martin Collins article in Stereophile around 1998 IIRC. Prior to that, Matti Otalla’s work also caused some issues. I wrote about this stuff here https://hifisonix.com/the-case-for-feedback/
In the feedback discussion, Bruno Putzeys F-Word article is the best short summation of the subject.
In the feedback discussion, Bruno Putzeys F-Word article is the best short summation of the subject.
Elektor had a low feedback design in 1988, I think that's where I first read about TIM and the supposed ill effect of strong overall feedback (although I vaguely remember another article from the 1980's about the same subject). The rationale was that stuff about slewing from Daugherty and Greiner's 1966 article, that was repeated by Otala in the early 1970's and debunked by Peter Garde in 1977-1978.
Sorry, I guess that was rude.
A feedback amplifier amplifies the error signal, which is the difference between the input signal and a scaled sample of the output signal. There is an integrator in the loop that in effect sums up the error signal over time and continuously pushes the output towards the desired value. You can put a delay in the loop and it will continue to function properly provided the stability conditions are met.
Here's an analogy. Think about driving a car. You watch the center line of the lane and constantly compare it to the position of the car. That's your error signal. If the car drifts to the right, you nudge the steering wheel to the left. If it drifts to the left, you steer to the right. It takes you time to react, and time for the car to respond to steering inputs. The car never tracks the lane perfectly, but provided the road doesn't twist too sharply, you can reliably keep from swerving out of your lane -- in spite of the delays.
It's intuitively obvious that feedback can't work, because the error correction always arrives after the fact. The intuition is also totally wrong. To understand why, you need to learn some non-trivial math. If you don't know what a Laplace transform is, well, let's just say the answers are out there.
A feedback amplifier amplifies the error signal, which is the difference between the input signal and a scaled sample of the output signal. There is an integrator in the loop that in effect sums up the error signal over time and continuously pushes the output towards the desired value. You can put a delay in the loop and it will continue to function properly provided the stability conditions are met.
Here's an analogy. Think about driving a car. You watch the center line of the lane and constantly compare it to the position of the car. That's your error signal. If the car drifts to the right, you nudge the steering wheel to the left. If it drifts to the left, you steer to the right. It takes you time to react, and time for the car to respond to steering inputs. The car never tracks the lane perfectly, but provided the road doesn't twist too sharply, you can reliably keep from swerving out of your lane -- in spite of the delays.
It's intuitively obvious that feedback can't work, because the error correction always arrives after the fact. The intuition is also totally wrong. To understand why, you need to learn some non-trivial math. If you don't know what a Laplace transform is, well, let's just say the answers are out there.
Another analogy would be the way an airplane fights drag with power to come to an equilibrium of speed. If you add power the plane doesn't go faster and faster, it has more drag produced and so comes to a higher but stable speed. So when FB makes it back to the input so quickly that the distortion components are reduced as they are produced, they adjust against each other at the speed of electricity in the amplification leg, and come into equilibrium because it is a closed loop and the energy just follows physical laws, Ohm's law.
The signal has a value and a derivative at any point in time. This derivative allows the system to compute the input at a (very short) moment later (using the phase correction capacitor in the feedback, (which does act as an integrator being in the Fdbk). So the correction arrives at the input in time coherence with that new input. (well, the actual correction comes from subtracting those two signals) So the actual loop propagation time is compensated for by the derived predictive correction. So the N Fdbk acts as if immediately applied, as long as the signal has not changed faster than the derivative would predict. Just another way of looking at the operation. There still is some propagation time around the loop, it's just correcting for where the signal will be when it gets there.
The car driver models where the car will be so as to be timely in applying the correction. Same thing.
The car driver models where the car will be so as to be timely in applying the correction. Same thing.
Last edited:
Yes, that sounds approximately right. To be honest, I don't really understand what the argument here is, though. I should probably read the whole thread more carefully.
There's no such thing as an infinite-bandwidth amplifier, so the forward path will always look like an integrator. Neglecting propagation delay, the feedback is continuous and instantaneous. Even with an aggressive low-pass filter in the forward path, the output starts to change as soon as the input changes. It's just the rise time that's different. I think maybe Cordell made this point in his "Another View of TIM" article back in 1980. As long as you satisfy the Nyquist criterion, the loop will be stable and you won't have any "echoes" or anything like that, i.e., no signs of "re-entrant" behavior on the scope. You can add a F(s) = e^-sT term to the forward gain equation to model propagation time and then solve for the closed loop transfer function. The propagation delay is so small in our applications as to be negligible.
I understand it's basically impossible to solve the loop equations analytically once you include non-linear distortion and noise. All that is beyond my sorely-eroded math skills at this point anyway.
Again, without really understanding the point of contention here, I think there are some really important intuitions you need to debate this topic. The first is the difference between delay and phase shift. The second is that an open-loop amplifier is qualitatively different than a feedback amplifier. Both are effectively analog computers. The former is computing the product of the input signal times a constant (ideally). The latter is solving for the minimum error between the input and a scaled sample of the output.
IMHO, this is actually a pretty damned complicated business and it's best discussed in the context of formal control systems theory. You know, Laplace transforms, poles and zeros, and whatnot.
I designed and built a headphone amplifier (admittedly, I cribbed the core design from Bob Cordell) that SPICE claims has 130dB of loop gain. It's incredibly stable and sounds utterly clean and transparent, and not at all bright or harsh. I was flabbergasted that it never showed a hint of oscillation or overshoot from the very first time I turned it on. I subsequently built a highly-lauded low feedback amplifier to compare, and it was just no contest.
I think it's likely that a carefully "voiced" low feedback amplifier can sound very good, probably for psychoacoustic reasons. Just like I prefer the look of film to high-definition video. But in my experience, a well-done feedback amplifier is for all intents and purposes sonically perfect.
Feedback theory is lovely, and I am fated to die without ever understanding more than a small part of the subject. Oh well. I am satisfied knowing smarter people than me have sorted it all out.
There's no such thing as an infinite-bandwidth amplifier, so the forward path will always look like an integrator. Neglecting propagation delay, the feedback is continuous and instantaneous. Even with an aggressive low-pass filter in the forward path, the output starts to change as soon as the input changes. It's just the rise time that's different. I think maybe Cordell made this point in his "Another View of TIM" article back in 1980. As long as you satisfy the Nyquist criterion, the loop will be stable and you won't have any "echoes" or anything like that, i.e., no signs of "re-entrant" behavior on the scope. You can add a F(s) = e^-sT term to the forward gain equation to model propagation time and then solve for the closed loop transfer function. The propagation delay is so small in our applications as to be negligible.
I understand it's basically impossible to solve the loop equations analytically once you include non-linear distortion and noise. All that is beyond my sorely-eroded math skills at this point anyway.
Again, without really understanding the point of contention here, I think there are some really important intuitions you need to debate this topic. The first is the difference between delay and phase shift. The second is that an open-loop amplifier is qualitatively different than a feedback amplifier. Both are effectively analog computers. The former is computing the product of the input signal times a constant (ideally). The latter is solving for the minimum error between the input and a scaled sample of the output.
IMHO, this is actually a pretty damned complicated business and it's best discussed in the context of formal control systems theory. You know, Laplace transforms, poles and zeros, and whatnot.
I designed and built a headphone amplifier (admittedly, I cribbed the core design from Bob Cordell) that SPICE claims has 130dB of loop gain. It's incredibly stable and sounds utterly clean and transparent, and not at all bright or harsh. I was flabbergasted that it never showed a hint of oscillation or overshoot from the very first time I turned it on. I subsequently built a highly-lauded low feedback amplifier to compare, and it was just no contest.
I think it's likely that a carefully "voiced" low feedback amplifier can sound very good, probably for psychoacoustic reasons. Just like I prefer the look of film to high-definition video. But in my experience, a well-done feedback amplifier is for all intents and purposes sonically perfect.
Feedback theory is lovely, and I am fated to die without ever understanding more than a small part of the subject. Oh well. I am satisfied knowing smarter people than me have sorted it all out.
Actually, that doesn't sound quite right. There's no prediction going on in a negative feedback loop. I'm not really invested enough in this to get into an argument. I just encourage people to have faith in the theory, which is well sorted out by now.
The discussions have been long and convoluted. Most of the issues argued over probably don't have much real impact, they often are near equivalent but viewed differently. The issue of re-entrant higher harmonic distortion at low N Fdbk (and high amplifier distortion), as shown in the JLH and Baxandall graphs earlier, is a real concern since tube amps tend to have low N Fdbk if they have any. The existence of this re-entrant distortion leads one to think there is time delayed looping going on. But the correction for time offset in N Fdbk leads one to not believe in time delay. This contrast in perception seems to drive the No Fdbk versus Fdbk arguments endlessly. It's important to further see that the severity of this re-entrant distortion is proportional to amplifier inherent distortion and disproportional to the amount of N Fdbk. A happy median can be found.
The Cordell graph is somewhat mis-leading, since it starts with a low distortion amplifier as the "0" dB of N Fdbk, but probably already has 20 dB of local degeneration internally, un-accounted for. That does seem to point to some disparity in the types of N Fdbk, since those local actions are typically low Fdbk but don't seem to set off re-entrant higher harmonics. It would be good if we understood what works cleanly and what does not.
------------------------------------------------------------
If the car is drifting to one side of the lane at some rate, that is derivative info. We certainly use that in driving. You know your going off the road if you don't fix that.
The Cordell graph is somewhat mis-leading, since it starts with a low distortion amplifier as the "0" dB of N Fdbk, but probably already has 20 dB of local degeneration internally, un-accounted for. That does seem to point to some disparity in the types of N Fdbk, since those local actions are typically low Fdbk but don't seem to set off re-entrant higher harmonics. It would be good if we understood what works cleanly and what does not.
------------------------------------------------------------
If the car is drifting to one side of the lane at some rate, that is derivative info. We certainly use that in driving. You know your going off the road if you don't fix that.
Last edited: