What frequency and Q should be used when trying to model room gain on a program like ported.xls. I am trying to design a sub box with a little hum in the 30-40hz range. I am doing this because my sub will have a fixed crossover of 80hz. My mains have an F3 of 65 so by building a box with a hump at the lower frequencies I will affectively lower the 80hz crossover to the 65hz I need. I don't want to go too far with the hump because of room gain in the lower frequencies.
I don't know anything about ported.xls, but this thread may help a bit. Plenty to be found on a search for 'room gain' btw.
http://www.diyaudio.com/forums/showthread.php?s=&threadid=54031&perpage=10&highlight=&pagenumber=1
hth,
Rob
http://www.diyaudio.com/forums/showthread.php?s=&threadid=54031&perpage=10&highlight=&pagenumber=1
hth,
Rob
The standard rule of thumb is to use Q=0.6 to 0.7 and frequency = C/(2*L) where C is the speed of sound and L is the longest dimension of your room in units that match the length units....
For a 20 foot longest dimension, use:
1130/(2*20)=F=1130/40=28Hz
for 4 meter longest dimension, use:
345/(2*4)=F=345/8=43Hz
It is difficult to say what actual room gain will be in any instance, as it depends on: 1) above the frequency you just calculated on placement of woofers and your ears; and 2) below that frequency by how solid the walls are and what amount of leakage there is.; 3) At all frequencies it depends on how much your room differs from the ideal reflective shoebox.
In a sense, it is not all that predictable, but a program which does it better than any other freebie available is found at the FRD Consortium. Look for the RRC or Room Response Calculator.
For a 20 foot longest dimension, use:
1130/(2*20)=F=1130/40=28Hz
for 4 meter longest dimension, use:
345/(2*4)=F=345/8=43Hz
It is difficult to say what actual room gain will be in any instance, as it depends on: 1) above the frequency you just calculated on placement of woofers and your ears; and 2) below that frequency by how solid the walls are and what amount of leakage there is.; 3) At all frequencies it depends on how much your room differs from the ideal reflective shoebox.
In a sense, it is not all that predictable, but a program which does it better than any other freebie available is found at the FRD Consortium. Look for the RRC or Room Response Calculator.
Hmmmmm, my guess would be your chances of getting that to be optimal or even close are similar to trying to pin the tail on the donkey blindfolded in an arena with a 30 second time limit!
The difference between simulated and measured room gain in my case has been so big, the simulations are worthless. Further, room modes are the same and complicate it further.
80 Hz is quite high for a subwoofer xo IMO, you really need to get a variable xo point at the very least. It's not difficult to achieve or expensive.
The difference between simulated and measured room gain in my case has been so big, the simulations are worthless. Further, room modes are the same and complicate it further.
80 Hz is quite high for a subwoofer xo IMO, you really need to get a variable xo point at the very least. It's not difficult to achieve or expensive.
room gain
The best advise I know is just to measure room gain.
There are just too many variables to try and simulate, unless you live in a reiforced concrete box with no windows or ventilation.
The best advise I know is just to measure room gain.
There are just too many variables to try and simulate, unless you live in a reiforced concrete box with no windows or ventilation.
Cabin Gain / Room Gain - interesting topic for small spaces
Sorry for bumping this old thread, but I could find any current discussion on this topic (except for a few off topic references in threads discussing other things), and I think it is an interesting subject.
Assuming I did live in a rectangular cuboid, with walls built of massive concrete and no furniture, how would the transfer function for strictly room gain (ignoring boundary gain) look?
While I realize you'd never achieve this exact transfer function in reality, but I'd like to know how this fairly simple theoretical situation would model.
I'm going to assume the transfer function looks VERY VAGUELY something like this:
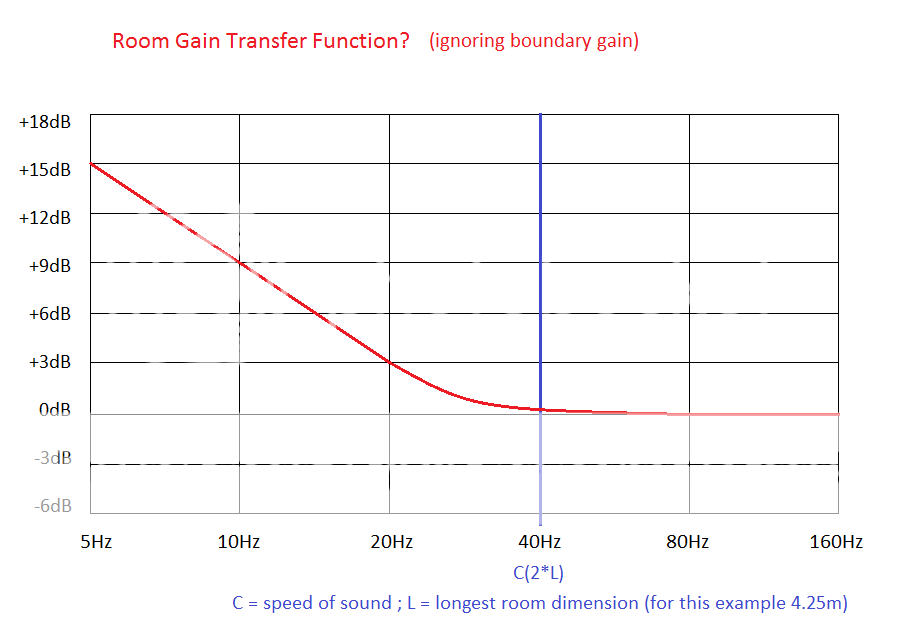
But what would the exact slope be? (I heard somehwere 3dB/oct - is this possible?). Where would the +3dB frequency be? Exactly at C/(2L), or would the transfer function still be 0dB there?
Has research been done on this subject? I would think so given how much this effect (also known as cabin gain) is used in automotive audio.
Sorry for bumping this old thread, but I could find any current discussion on this topic (except for a few off topic references in threads discussing other things), and I think it is an interesting subject.
The best advise I know is just to measure room gain.
There are just too many variables to try and simulate, unless you live in a reiforced concrete box with no windows or ventilation.
Assuming I did live in a rectangular cuboid, with walls built of massive concrete and no furniture, how would the transfer function for strictly room gain (ignoring boundary gain) look?
While I realize you'd never achieve this exact transfer function in reality, but I'd like to know how this fairly simple theoretical situation would model.
I'm going to assume the transfer function looks VERY VAGUELY something like this:

But what would the exact slope be? (I heard somehwere 3dB/oct - is this possible?). Where would the +3dB frequency be? Exactly at C/(2L), or would the transfer function still be 0dB there?
Has research been done on this subject? I would think so given how much this effect (also known as cabin gain) is used in automotive audio.
"Room gain" does not actually have a curve. It is constant - a straight line. The SPL is the ratio of the difference in air pressure in the room between "cone in" and "cone out". For a given pressure difference, the "room gain" or "pressurisation" SPL is constant regardless of frequency. (*)
To see where the often-quoted "room gain curve" comes from, consider how a speaker works. To maintain a constant SPL (flat response) in "free air" (no room boundaries), the cone must quadruple its excursion for each halving of frequency. But when you place such a speaker in a room, the quadrupling of excursion causes a pressurisation SPL increase. So a speaker that is flat in "free space" will show a 12 dB per octave SPL increase in a closed room. The smaller the room, the higher the frequency at which the effect will start to become significant. Working backwards, in free space the room gain will be zero.
Having established the rules, we can now work out the frequency at which room gain starts to become significant - the frequency at which room gain is adding 6 dB to the
overall SPL. This is the frequency where the free air SPL of the speaker and the pressurisation SPL of the speaker are equal. For example, if the free air SPL of a speaker at a given frequency is 120 dB, and the pressurisation SPL is 120 dB, the total SPL is 126 dB.
(*) Important note: the above is only correct to a first approximation. It neglects the differences in SPL that occur due to room resonances and directivity.
For much more discussion, and the actual formulas required to do the calculations, I recommend these threads:
http://www.diyaudio.com/forums/multi-way/5668-volume-displacement-spl-chart.html
http://www.diyaudio.com/forums/multi-way/1995-calculating-room-gain.html
http://www.diyaudio.com/forums/multi-way/1261-room-gain.html
To see where the often-quoted "room gain curve" comes from, consider how a speaker works. To maintain a constant SPL (flat response) in "free air" (no room boundaries), the cone must quadruple its excursion for each halving of frequency. But when you place such a speaker in a room, the quadrupling of excursion causes a pressurisation SPL increase. So a speaker that is flat in "free space" will show a 12 dB per octave SPL increase in a closed room. The smaller the room, the higher the frequency at which the effect will start to become significant. Working backwards, in free space the room gain will be zero.
Having established the rules, we can now work out the frequency at which room gain starts to become significant - the frequency at which room gain is adding 6 dB to the
overall SPL. This is the frequency where the free air SPL of the speaker and the pressurisation SPL of the speaker are equal. For example, if the free air SPL of a speaker at a given frequency is 120 dB, and the pressurisation SPL is 120 dB, the total SPL is 126 dB.
(*) Important note: the above is only correct to a first approximation. It neglects the differences in SPL that occur due to room resonances and directivity.
For much more discussion, and the actual formulas required to do the calculations, I recommend these threads:
http://www.diyaudio.com/forums/multi-way/5668-volume-displacement-spl-chart.html
http://www.diyaudio.com/forums/multi-way/1995-calculating-room-gain.html
http://www.diyaudio.com/forums/multi-way/1261-room-gain.html
Last edited:
klanky,
I've seen a few different theoretical "room gain curves" with a nice neat curve like you have shown. But when you see measurements from a real room you realise how pointless it is considering this curve. Add to your curve a 20 db peak at 35 Hz, then a 15 db dip at 55 then numerous peaks and dips between there and 200 Hz. It becomes difficult if not impossible to say if there is actually any gain now. If you eq out the lowest dip, you then find that your sub that is flat to 20 Hz anechoic now needs 12db of eq to reach 20 Hz flat in room! The room modes dominate.
So my suggestion is forget room gain! Get a mic and mic preamp and REW and measure. You can see what your room gain is by measuring the sub nearfield (mic almost touching the cone) then in your listening position. The difference between the two is your room gain combined with room modes. It's easy to do and you'll get real and useful data.
I've seen a few different theoretical "room gain curves" with a nice neat curve like you have shown. But when you see measurements from a real room you realise how pointless it is considering this curve. Add to your curve a 20 db peak at 35 Hz, then a 15 db dip at 55 then numerous peaks and dips between there and 200 Hz. It becomes difficult if not impossible to say if there is actually any gain now. If you eq out the lowest dip, you then find that your sub that is flat to 20 Hz anechoic now needs 12db of eq to reach 20 Hz flat in room! The room modes dominate.
So my suggestion is forget room gain! Get a mic and mic preamp and REW and measure. You can see what your room gain is by measuring the sub nearfield (mic almost touching the cone) then in your listening position. The difference between the two is your room gain combined with room modes. It's easy to do and you'll get real and useful data.
"Room gain" does not actually have a curve. It is constant - a straight line. The SPL is the ratio of the difference in air pressure in the room between "cone in" and "cone out". For a given pressure difference, the "room gain" or "pressurisation" SPL is constant regardless of frequency. (*)
To see where the often-quoted "room gain curve" comes from, consider how a speaker works. To maintain a constant SPL (flat response) in "free air" (no room boundaries), the cone must quadruple its excursion for each halving of frequency. But when you place such a speaker in a room, the quadrupling of excursion causes a pressurisation SPL increase. So a speaker that is flat in "free space" will show a 12 dB per octave SPL increase in a closed room. The smaller the room, the higher the frequency at which the effect will start to become significant. Working backwards, in free space the room gain will be zero.
For much more discussion, and the actual formulas required to do the calculations, I recommend these threads:
Thank you for that information, I think that is a good explanation of what the physical model is that the effect stems from. When I have more time I'll try to work out some of the math, and see if I can come up with some figures.
I've seen a few different theoretical "room gain curves" with a nice neat curve like you have shown. But when you see measurements from a real room you realise how pointless it is considering this curve.
So my suggestion is forget room gain! Get a mic and mic preamp and REW and measure.
Granted, I don't actually expect to gain any directly applicable figures in practice, but I'm interested in the underlying theoretical (physical) model of the phenomenon.
The room modes dominate.
I was under the impression that below C/2L there are no more room modes?
Between the lowest mode, which is often around 35 Hz or so and 200 Hz room modes dominate the response. The lowest mode is easy to see in measurements.
Fair enough if this is purely for academic theoretical interest. For any practical situation it hardly seems worth considering. To me it's a bit like comparing cheap vs expensive wines while skydiving.
Granted, I don't actually expect to gain any directly applicable figures in practice, but I'm interested in the underlying theoretical (physical) model of the phenomenon.
Fair enough if this is purely for academic theoretical interest. For any practical situation it hardly seems worth considering. To me it's a bit like comparing cheap vs expensive wines while skydiving.
What frequency and Q should be used when trying to model room gain on a program like ported.xls. I am trying to design a sub box with a little hum in the 30-40hz range. I am doing this because my sub will have a fixed crossover of 80hz. My mains have an F3 of 65 so by building a box with a hump at the lower frequencies I will affectively lower the 80hz crossover to the 65hz I need. I don't want to go too far with the hump because of room gain in the lower frequencies.
Hmm...
I REALLY must update that ported.xls on my site. The one I'm using allows you to add the measured "transfer function" for your room to the simulated alignment's response, which should give a clearer picture of what the likely end-result would be in your room.
- Status
- Not open for further replies.
- Home
- General Interest
- Room Acoustics & Mods
- modeling room gain