Would someone like to suggest one of the following:
A formula for determining the volume of an isosceles tetrahedron, NOT the formula for determining the volume of a regular tetrahedron NOR for the irregular non-isosceles?
A calculator or modeler of some sort that will do it graphically?
A website that has the actual formula spelled out?
Or solve this problem:
The outside measurements of a 3/4" thick wood base are equilaterally 21". What are the measurements of the 3 isosceles triangles which will give the resulting tetrahedron 1.5 cubic feet (don't neglect the wood thickness)? Show your work so I can steal the formula. 😉
Much appreciated.
Dave
A formula for determining the volume of an isosceles tetrahedron, NOT the formula for determining the volume of a regular tetrahedron NOR for the irregular non-isosceles?
A calculator or modeler of some sort that will do it graphically?
A website that has the actual formula spelled out?
Or solve this problem:
The outside measurements of a 3/4" thick wood base are equilaterally 21". What are the measurements of the 3 isosceles triangles which will give the resulting tetrahedron 1.5 cubic feet (don't neglect the wood thickness)? Show your work so I can steal the formula. 😉
Much appreciated.
Dave
Thread
So let me get this straight,
The isosceles tetrahedron has an equilateral triangle as a base, with edge length of 21"?
If that's the case then the isosceles triangles should have one edge at 21" and the isosceles edges at 63.325"
I just used a ProE model and changed the height of the tetrahedron until the enclosed volume was the right value, this does incorporate the thickness of the box.
I'm sure there's some formula out there you could modify, but since you're doing it an odd way you might need to do some sort of iterative solution anyhow.
So let me get this straight,
The isosceles tetrahedron has an equilateral triangle as a base, with edge length of 21"?
If that's the case then the isosceles triangles should have one edge at 21" and the isosceles edges at 63.325"
I just used a ProE model and changed the height of the tetrahedron until the enclosed volume was the right value, this does incorporate the thickness of the box.
I'm sure there's some formula out there you could modify, but since you're doing it an odd way you might need to do some sort of iterative solution anyhow.
kneadle said:
IIRC the volume of any regular solid like this should be 1/6 x the area of the base x the height.
dave
The area of an equilateral triangle is A = 0.433 * X^2.
In this case x = 21 => A = 190.95sq.in.
The volume would be 0.433 * (the integral of X^2) from 0 to h, where h = height of the isosceles tetrahedron.
The desired volume is (V) = 1.5cu.ft. = 1728 * 1.5 = 2592cu.in.
Solving for h above
=> 2592 = 0.433 * (h^3/3)
=> h^3 = 17958.43
=> h = 26.187in.
This is the height of the isosceles tetrahedron
By trig, the edge of each side is 28.857in. and 21in. at the base.
Rodd Yamashita
In this case x = 21 => A = 190.95sq.in.
The volume would be 0.433 * (the integral of X^2) from 0 to h, where h = height of the isosceles tetrahedron.
The desired volume is (V) = 1.5cu.ft. = 1728 * 1.5 = 2592cu.in.
Solving for h above
=> 2592 = 0.433 * (h^3/3)
=> h^3 = 17958.43
=> h = 26.187in.
This is the height of the isosceles tetrahedron
By trig, the edge of each side is 28.857in. and 21in. at the base.
Rodd Yamashita
Re: Re: isosceles tetrahedron formula
Thanks all, but see the bottom of this post because I got two quite different answers. BTW, Here's why I asked in the first place: http://mathforum.org/dr.math/faq/formulas/faq.irreg.tetrahedron.html Upon seeing this, my eyes glazed over.
I don't think an isosceles tetrahedron is a regular solid. If it is, then I have never seen it described as such. You can see by Roddyama's response above that it is a little more complicated than solving for a regular solid.
Ok. Do you two guys wanna wrestle for it? 😀
Dave
Thanks all, but see the bottom of this post because I got two quite different answers. BTW, Here's why I asked in the first place: http://mathforum.org/dr.math/faq/formulas/faq.irreg.tetrahedron.html Upon seeing this, my eyes glazed over.
planet10 said:
I don't think an isosceles tetrahedron is a regular solid. If it is, then I have never seen it described as such. You can see by Roddyama's response above that it is a little more complicated than solving for a regular solid.
Ok. Do you two guys wanna wrestle for it? 😀
Dave
Discrepancy
I think the difference is I account for a box in my calculations. The 1.5 cubic feet is the volume inside the box, and the 21" edge length and 63" edge length are the outside edge lengths of the box.
Using the dimensions of the inside tetrahedron (the dimensions of the volume) with edge lengths 18.14" and 55.57" I double-checked with the matrix formula and my answer is correct unless there's some other mistake.
1.0e+003 *
0 0.3291 0.3291 3.0880 0.0010
0.3291 0 0.3291 3.0880 0.0010
0.3291 0.3291 0 3.0880 0.0010
3.0880 3.0880 3.0880 0 0.0010
0.0010 0.0010 0.0010 0.0010 0
The determinant of that matrix is 1.9350e+009
1.9350e+009 = 288 * V^2
Therefore V = 2.5920e+003 in^3 = 1.5 ft^3
I think the difference is I account for a box in my calculations. The 1.5 cubic feet is the volume inside the box, and the 21" edge length and 63" edge length are the outside edge lengths of the box.
Using the dimensions of the inside tetrahedron (the dimensions of the volume) with edge lengths 18.14" and 55.57" I double-checked with the matrix formula and my answer is correct unless there's some other mistake.
1.0e+003 *
0 0.3291 0.3291 3.0880 0.0010
0.3291 0 0.3291 3.0880 0.0010
0.3291 0.3291 0 3.0880 0.0010
3.0880 3.0880 3.0880 0 0.0010
0.0010 0.0010 0.0010 0.0010 0
The determinant of that matrix is 1.9350e+009
1.9350e+009 = 288 * V^2
Therefore V = 2.5920e+003 in^3 = 1.5 ft^3
Re: Discrepancy
...and I was worried that I wouldn't have room to properly port the box!
5 ft 3 in? I've got to work on my sales technique to the wifey before I start construction on these mamas.
Thanks tons,
Dave
PS--do you know where the two different calculations are off? Even if Roddyama didn't take into account the inside of the box, his is still much different than yours.
MITMechE said:
...and I was worried that I wouldn't have room to properly port the box!
5 ft 3 in? I've got to work on my sales technique to the wifey before I start construction on these mamas.
Thanks tons,
Dave
PS--do you know where the two different calculations are off? Even if Roddyama didn't take into account the inside of the box, his is still much different than yours.
The differences most likely resulted from a couple of things:
Using 21" edge length instead of 18.14" for the base
Not accounting for the box itself.
They probably aren't off as much as they look, the truth of the matter is a tall tetrahedron isn't a very efficient way of holding volume.
Using 21" edge length instead of 18.14" for the base
Not accounting for the box itself.
They probably aren't off as much as they look, the truth of the matter is a tall tetrahedron isn't a very efficient way of holding volume.
Well, thanks to yours and roddyama's supplied calculations, I can achieve a shorter and broader tetrahedron. In addition, 1.5 cu ft was the absolute maximum for the driver in question. It will still sound good (given a skillful construction) with much less volume. I'll advise as things progress.
Keep a lookout for "tetrahedron DIY project finished" in the next few weeks, and I'll be sure to post photos and credits.
Thanks
Dave
Keep a lookout for "tetrahedron DIY project finished" in the next few weeks, and I'll be sure to post photos and credits.
Thanks
Dave
Re: Re: Discrepancy
Mine was a guess pulled from my head (from info stored there a long time ago). If Rod solved the integral correctly then i probably just mis-remembered. Maybe the 1/6 should be 1/3?
dave
kneadle said:
Mine was a guess pulled from my head (from info stored there a long time ago). If Rod solved the integral correctly then i probably just mis-remembered. Maybe the 1/6 should be 1/3?
dave
Re: Re: Re: Discrepancy
Are you SURE you're not thinking equilateral tetrahedron? Because if you're SURE that an isosceles tetrahedron is a regular solid, then my problems are over.
Dave
planet10 said:
Are you SURE you're not thinking equilateral tetrahedron? Because if you're SURE that an isosceles tetrahedron is a regular solid, then my problems are over.
Dave
Re: Re: Re: Re: Discrepancy
Ya i think i'm just out to lunch. Perhaps your use of the word tetrahedron made me not think it thru since it won't be a tetrahedron without having sides that are 4 identical equalateral triangles.
dave
kneadle said:
Ya i think i'm just out to lunch. Perhaps your use of the word tetrahedron made me not think it thru since it won't be a tetrahedron without having sides that are 4 identical equalateral triangles.
dave
I don't mean to laugh, but any four-sided solid is a tetrahedron. There's the equilateral tetrahedron, the isosceles tetrahedron and the true irregular tetrahedron.
I love this forum, though. You, in particular, are very helpful. I read a lot of your posts and, in the process, have learned a lot.
I'm still porting this design...
Dave
I love this forum, though. You, in particular, are very helpful. I read a lot of your posts and, in the process, have learned a lot.
I'm still porting this design...
Dave
OK, just call me out to lunch today...
I used to eat this stuff for breakfast (Honours Degree in Math) 😀
dave
I used to eat this stuff for breakfast (Honours Degree in Math) 😀
dave
Trying to imagine, first, not achieve
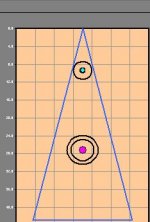
I have a pair of equilateral tetrahedron speakers, which have been destroyed in the course of history. I want to keep the tetrahedronal concept, but design them better. The picture is the front baffle with a 6 1/2" Vifa P17WG00-06 and a Vifa D27TG05-06 aligned.
There will be a total of 4 baffles (if this idea survives). The bottom one will be an equilateral triangle of 21" or so (it needs to be reasonably narrow). The other three are shaped exactly the same, like the one pictured, creating a reasonable volume in the shape of an isosceles tetrahedron to let the woofer speak. You basically see the front baffle, and that's it, as shown. However, as was pointed out, it's hard to come up with enough volume in a tetrahedron.
Right now I haven't bought anything but the drivers, so I'm only imagining. In fact, I'm quite intrigued by the T-Line concept, and would like to e-mail planet10 if he will not be against private e-mails.
Tetrahedra are soooo sexy, though. The wife wants them painted white with pictures of clouds and rainbows on them.
Dave
I have a pair of equilateral tetrahedron speakers, which have been destroyed in the course of history. I want to keep the tetrahedronal concept, but design them better. The picture is the front baffle with a 6 1/2" Vifa P17WG00-06 and a Vifa D27TG05-06 aligned.
There will be a total of 4 baffles (if this idea survives). The bottom one will be an equilateral triangle of 21" or so (it needs to be reasonably narrow). The other three are shaped exactly the same, like the one pictured, creating a reasonable volume in the shape of an isosceles tetrahedron to let the woofer speak. You basically see the front baffle, and that's it, as shown. However, as was pointed out, it's hard to come up with enough volume in a tetrahedron.
Right now I haven't bought anything but the drivers, so I'm only imagining. In fact, I'm quite intrigued by the T-Line concept, and would like to e-mail planet10 if he will not be against private e-mails.
Tetrahedra are soooo sexy, though. The wife wants them painted white with pictures of clouds and rainbows on them.
Dave
Attachments
Ahhh, now I understand!😉 Pyramid Power!!
So will you be using them to keep your razor blades sharp as well?😀
So will you be using them to keep your razor blades sharp as well?😀
We're having a baby, so there has to be a foam ball on the tippy-top to prevent baby from impaling herself...
...or Daddy, when he's trying to open a window or get a book.
...or Daddy, when he's trying to open a window or get a book.
- Status
- Not open for further replies.