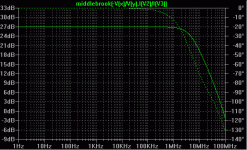
Steve Eddy said:Oh, by the way, the question isn't simply how much feedback is employed in the CFP, but relative to the Darlington.
Okay, but I'm assuming that by the "loop gain" of the darlington, you mean gm1 * (beta2 + 1) RL, that is, the loop gain of only the first stage? 'Cause that's the only loop that I can conceive of with of the darlington. At any rate, that will need to be computed manually (no problem, since we have the formula above already, assuming you agree with it). The Middlebrook stuff with SPICE assumes there's a physical interconnection you can identify as the loop. There's an identifiable loop with a simple EF, but only if you tap inside the linearized hybrid pi model, which on my freeware simulator isn't directly accessible. (The parameter values are accessible, but you'd have to construct the model yourself from controlled sources). With the CFP I can use subcircuit replication with the full-up Middlebrook techniquie.
As I'm writing this I'm starting to realize what you were trying to say with your earlier post. It seems like the first stage of the darlington will have much lower distortion than the second because of the (beta2 + 1) multiplier of its loop gain. But you end up cascading it with a normal EF, so it would appear that any potential distortion reduction from the increased loop gain of the first stage would be lost with the cascade. Anyway, I'm going to sign off...