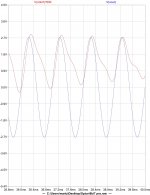
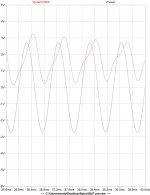
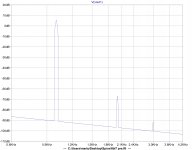
Here are two plots I made of a circuit output plotted with the best residual I could get using a series pair of loop back double t notches at the fundamental.
The circuit is push pull and nulls 2H with equal drive and identical components. When the drive is unbalanced one way I get the first of the residuals shown and unbalanced the other I get the second residual shown. The delay I applied to the unfiltered output could be wrong so probably best ignored but is the same for both plots
The question I have is.... by looking at the residual (red) can you tell if the phase of the 2H is reversed between them?
Figured this was the best place to ask since NP turned me on to the idea of 2H phase. The FFT plot is what get I no matter which way I adjust the drive balance.
Thanks in advance,
Marty
The circuit is push pull and nulls 2H with equal drive and identical components. When the drive is unbalanced one way I get the first of the residuals shown and unbalanced the other I get the second residual shown. The delay I applied to the unfiltered output could be wrong so probably best ignored but is the same for both plots
The question I have is.... by looking at the residual (red) can you tell if the phase of the 2H is reversed between them?
Figured this was the best place to ask since NP turned me on to the idea of 2H phase. The FFT plot is what get I no matter which way I adjust the drive balance.
Thanks in advance,
Marty
Attachments
I think I can see the doubled frequency. The filter Q is high but I still see the fundamental in the residual when I multiply it 600 times. I have not been having any fun trying to align them as the filter takes a while to settle down. Tried to filter it with just math in LT spice but can't figure it out.
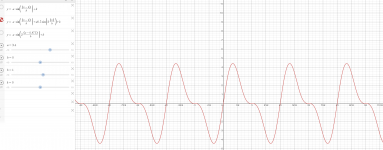
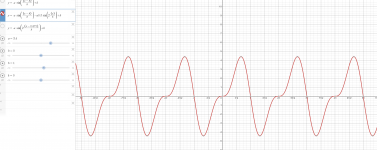
The first picture is of the form: f(x) = sin(x)+|a|*sin(2x) (one could say positive H2)
The second picture is of the form: f(x) sin(x) -|a|*sin(2x) (one could say negative H2)
In the above H2 is both positive and negative in one half cycle of the fundamental. Only the succession changes.
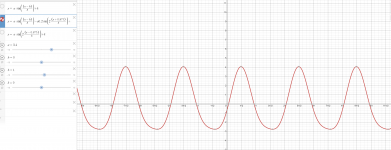
According to Papas definition positive H2: H2 is positive, when fundamental is positive and H2 is positive, when fundamental is negative. With a phase -Pi/4 shift the maxima coincide.
f(x) = sin(x)+|a|*sin(2x - Pi/4)
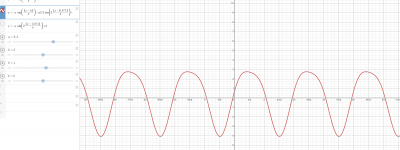
According to Papas definition negative H2: H2 is negative, when fundamental is positive and H2 is negative, when fundamental is negative. With a phase +Pi/4 shift the minima coincide.
f(x) = sin(x)+|a|*sin(2x + Pi/4)
I do not know, if phase shifts of +/- Pi/4 can be introduced by transistors, but thats how I understood it.
Here you can play with the functions:
Sine Wave
The second picture is of the form: f(x) sin(x) -|a|*sin(2x) (one could say negative H2)
In the above H2 is both positive and negative in one half cycle of the fundamental. Only the succession changes.
According to Papas definition positive H2: H2 is positive, when fundamental is positive and H2 is positive, when fundamental is negative. With a phase -Pi/4 shift the maxima coincide.
f(x) = sin(x)+|a|*sin(2x - Pi/4)
According to Papas definition negative H2: H2 is negative, when fundamental is positive and H2 is negative, when fundamental is negative. With a phase +Pi/4 shift the minima coincide.
f(x) = sin(x)+|a|*sin(2x + Pi/4)
I do not know, if phase shifts of +/- Pi/4 can be introduced by transistors, but thats how I understood it.
Here you can play with the functions:
Sine Wave
Attachments
Last edited:
I have learned that amplifiers can have phase or delay distortion as well. So we can have positive and negative H2 and anything inbetween. I also looked at some of Papas shots of the distortion curves and they too vary in phase for different amps. The notch filter used for measurement can have phase shifts too.
phase distortion
Above "formulas" are wrong: it must be Pi/2 instead of Pi/4 everywhere

phase distortion
Above "formulas" are wrong: it must be Pi/2 instead of Pi/4 everywhere

Very often the measuring filters will introduce that phase shift, for instance the
100 Hz hi-pass on the AP will shift the apparent phase of a 1 khz test.

100 Hz hi-pass on the AP will shift the apparent phase of a 1 khz test.

- Home
- Amplifiers
- Pass Labs
- Is the phase of 2H reversed in these two plots?