"To Infinity and Beyond"
Hi Bill,
I figured you did, that's why I mentioned it - I just couldn't resist 🙂.
I didn't anticipate that it would precipitate the infinite parabolic horn discussion that followed, though 🙂.
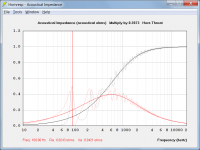
Together with Buzz Lightyear, Hornresp has no problem with infinity - the attachment shows the throat acoustical resistance and reactance of a representative finite parabolic horn (light traces) compared to the impedance of the same horn extended to infinity (dark traces).
Kind regards,
David
Hi Bill,
I figured you did, that's why I mentioned it - I just couldn't resist 🙂.
I didn't anticipate that it would precipitate the infinite parabolic horn discussion that followed, though 🙂.
Together with Buzz Lightyear, Hornresp has no problem with infinity - the attachment shows the throat acoustical resistance and reactance of a representative finite parabolic horn (light traces) compared to the impedance of the same horn extended to infinity (dark traces).
Kind regards,
David
Attachments
The parabolic horn is one of the two One-Parameter (1P) horns possible in cylindrical coordinates, and for that reason it is sometimes also called a cylindrical horn 🙂.
I kid you not - it's true. The parabolic horn is also sometimes called a cylindrical horn in the literature.
Yeah, but it has nothing to do with a parabola being the contour of the horn, as we are talking about it so far. It's a completely different thing.
And BTW, if there was a bounding cylinder to a parabola, the area expansion would tend to stop, right? That doesn't happen, the area just goes to infinity as well. As for the parabolic/cylindrical horn I guess - that's the reason why it's called that way - the expansion is the same.
And BTW, if there was a bounding cylinder to a parabola, the area expansion would tend to stop, right? That doesn't happen, the area just goes to infinity as well. As for the parabolic/cylindrical horn I guess - that's the reason why it's called that way - the expansion is the same.
Last edited:
Hi David,
The finite variety is sufficiently cylindrical as well.
Note the cylindrical ring at the mouth of this one.
Even at this short length, the differences in curvature and slope are becoming miniscule between it and the parabolic horn body.
If you extended this one out say to three feet or more, the differences would be unmeasurable even with a micrometer.
Regards,
Bill
Attachments
Last edited:
All separable coordinate systems with a finite origin must go to an elliptical cone for large distances from the origin. In the example here it must go to a circular cone since we are assuming axisymmetric.
"The parabolic horn is a true 1P horn if it is rectangular with two parallel sides, the two other sides expanding linearly, and the wave-fronts are concentric cylinders."
Horn Theory: An Introduction, Part 1
It is something completely different. The only similarity is the area expansion that goes linearly with distance for both.
In the picture WHG shows, there is a parabola as the contour (I assume), and that does not approach a cylinder in any imaginable sense of the word. For any cylinder with the same axis, it will cross its surface earlier or later. Then it will expand further.
Horn Theory: An Introduction, Part 1
It is something completely different. The only similarity is the area expansion that goes linearly with distance for both.
In the picture WHG shows, there is a parabola as the contour (I assume), and that does not approach a cylinder in any imaginable sense of the word. For any cylinder with the same axis, it will cross its surface earlier or later. Then it will expand further.
Last edited:
Unfortunately it has been shown (see Morse and Feshbach) that Webster's equation contains an assumption that limits its applicability to this discussion - basically it's wrong. So one should look to the more relevant approach using the wave equation, which gives very different answers to the questions. I don't understand why I have to keep pointing this out. (see chapter 6 in my book )
Earl, there has been misunderstanding in what a "parabolic horn" is in the first place. It is not a horn with a parabola as it contour. It's just a segment of cylindrical wave. Then it is 1P of course, but that's not the point.
More again.
So long as radius of the reference cylinder is commensurately expanding as well, the slope of the generating parabola will be getting closer to that of the adjoining cylinder, while both radii of curvature (transvers and longitudinal for the paraboloid, and transverse only for the cylinder) head toward infinity as well. Until they get their, the differences between the two surfaces continue to diminish. I never claimed the horn mouth (parabola leg spread) would not continue to expand with an increase in length; only that the cylinder radius would increase with that of the adjoining paraboloid.
Another way of looking at a parabola, is that it is a ellipse with its center at infinity.
WHG
So long as radius of the reference cylinder is commensurately expanding as well, the slope of the generating parabola will be getting closer to that of the adjoining cylinder, while both radii of curvature (transvers and longitudinal for the paraboloid, and transverse only for the cylinder) head toward infinity as well. Until they get their, the differences between the two surfaces continue to diminish. I never claimed the horn mouth (parabola leg spread) would not continue to expand with an increase in length; only that the cylinder radius would increase with that of the adjoining paraboloid.
Another way of looking at a parabola, is that it is a ellipse with its center at infinity.
WHG
Last edited:
You claimed:
This is simply not true and well ilustrates the point you tried to make. Now it seems you finally understand better. Congratulations.
You guys are good, sounds like Earl is trying to gain some understanding in order to improve the waveguide in his two-way, more power to ya.
I hope you know that there is only one finite source coordinate system that is 1P and that is spherical. All others are not 1P, so neither is a horn with a parabolic surface.
1P is the biggest error that Morse ever made (Vibration and Sound.) Fortunately he corrected it later on in his book Methods of Theoretical Physics where he highlights the errors of Webster's Equation and never even mentions 1P.
Last edited:
Oh. So a finite length of a cylindrical wave source, bounded by two planes perpendicular to its axis is not 1P? And what about a tube/cylinder driven with a flat wavefront, is that not a 1P?
Last edited:
Those are the two unique cases. A tube/cylinder is 1P, and the wave inside of a parallel plate circular cylinder is 1P, as you suggest, but if the walls of any waveguide curve then they cannot be 1P.
Basically there are two types of coordinate systems. Full 3D and 2D stretched along an infinite line. Only full 3D systems have finite origins for the radial coordinate (the direction of propagation), all others (except the two exceptions above) are infinite.
Basically there are two types of coordinate systems. Full 3D and 2D stretched along an infinite line. Only full 3D systems have finite origins for the radial coordinate (the direction of propagation), all others (except the two exceptions above) are infinite.
Last edited:
OK, but then that is what I was talking about. So it is 1P. But that was not the issue anyway.
I see. Thanks.
I see. Thanks.
Last edited:
Yea, they are 1P, but of no real interest to us. The circular cylinder one is only 1P if driven by a curved source oscillating radially - a virtual impossibility to create.
No, it was not the issue, but I would prefer if people would just give up on the concept of 1P - it can't happen in the real world.
No, it was not the issue, but I would prefer if people would just give up on the concept of 1P - it can't happen in the real world.