Earl Geddes has written recently. "You should certainly understand that in a linear system if I know the FR then I also know the transient response. Meaning that since they are just different ways of looking at the same thing it doesn't matter which one you talk about. Of course, I am assuming that we also know the phase, because there are some audible effects of phase on an impulse response, but you have made clear that you don't think that phase is audible, hence FR and transient response must be the same things."
I think a way to look at that mathematical truth is that if the upper frequencies are present like with good tweeters, then the whole system reacts real quick... which is like saying the transient response is swell.
Now there are lots of music systems with great tweeters, pretty flat FR, and yet flabby bass with lousy transient response. Yes, BR and TH we are looking at you.
Likewise, as everybody who has experimented with (or purchased) motional feedback subs, even with the same FR as other good systems, the transient response is tight and the bass "fast" (in a manner of speaking).
Is Earl's quote the final word or is there more to say about transient response than just the treble extension?
Thanks.
B.
I think a way to look at that mathematical truth is that if the upper frequencies are present like with good tweeters, then the whole system reacts real quick... which is like saying the transient response is swell.
Now there are lots of music systems with great tweeters, pretty flat FR, and yet flabby bass with lousy transient response. Yes, BR and TH we are looking at you.
Likewise, as everybody who has experimented with (or purchased) motional feedback subs, even with the same FR as other good systems, the transient response is tight and the bass "fast" (in a manner of speaking).
Is Earl's quote the final word or is there more to say about transient response than just the treble extension?
Thanks.
B.
It's a consequence of linear systems theory. In a linear time invariant system if you are given H(jw) you can calculate h(t) and vice versa. However, speaker cables + crossovers + loudspeaker drive units may not be 100.000 percent linear.
You will find phase compensation of the loudspeaker's low frequency roll-off (subject to certain provisos re room interactions) can audibly improve the transient response too. This might even be one of the "audible effects" to which Earl Geddes was referring and is probably the best example I can think of that shows transient response is more than just "treble extension".
If "FR" refers to the complex frequency response rather than just the magnitude response (that necessarily removes the phase information), then yes it affords a complete mathematical description. But for a description that better conveys what is audible, we have to consider (at least) the two-dimensions of the time-frequency plane where artefacts such as "flabby bass" can be portrayed.
If "FR" refers to the complex frequency response rather than just the magnitude response (that necessarily removes the phase information), then yes it affords a complete mathematical description. But for a description that better conveys what is audible, we have to consider (at least) the two-dimensions of the time-frequency plane where artefacts such as "flabby bass" can be portrayed.
The perceived transient response is depended on the rumbling decay afterwards i guess.
With a typical BR it resonates a little after the transient, depending of the total Q value of the system.
A "fast" system usually has a lower Q value.
With a typical BR it resonates a little after the transient, depending of the total Q value of the system.
A "fast" system usually has a lower Q value.
The perceived transient response is depended on the rumbling decay afterwards i guess.
With a typical BR it resonates a little after the transient, depending of the total Q value of the system.
A "fast" system usually has a lower Q value.
That is most of the important bit, but remember too that a linear phase alignment has no Q value...
We do need to be careful of ambiguity. "Transient response" in the linear systems sense is everything other than the input-forced, steady state response; the transient response characterizes the system itself apart from any particular input. So the "transient" response can have low-frequency components, depending on the masses and stiffnesses of the system elements. That's one way to see that "transient response" in the engineering sense is not synonymous with "treble extension".
This is intresting and almost a topic in it self, but somehow I cant really get past that in my expirience the transient response correlates poorly with the perception of "fast" or "tight" low frequency responce.Now there are lots of music systems with great tweeters, pretty flat FR, and yet flabby bass with lousy transient response. Yes, BR and TH we are looking at you.
It is hardly a secret that I'm partial to resonably high tuned (~40Hz) higher order quarterwave designs, where the transient response looks "horrible" compared to the stated ideal, yet I percieve them as "thighter" or "faster" and more tactile then most other designprinciples I have come across, if I'm alone in this then I'll leave it at that and remain happy, but if someone else have the same expirience then it becomes a bit more intresting.
Is there a gap between the linear steady state model of low frequency transient response depiction and our perception of the same?
We do need to be careful of ambiguity. "Transient response" in the linear systems sense is everything other than the input-forced, steady state response; the transient response characterizes the system itself apart from any particular input. So the "transient" response can have low-frequency components, depending on the masses and stiffnesses of the system elements. That's one way to see that "transient response" in the engineering sense is not synonymous with "treble extension".
Wholeheartedly agree with that. I am not even sure that the term "transient response" has any formal definition? It is often used instead of the impulse response - just as in the quote at the start of this thread.
Is there a gap between the linear steady state model of low frequency transient response depiction and our perception of the same?
No, but there is a "gap" in the common linking of perception to the way in which responses (linear or otherwise) are often portrayed.
No, but there is a "gap" in the common linking of perception to the way in which responses (linear or otherwise) are often portrayed.
This is, so far, the most civil and high-toned thread I can recall. And soundbloke seems, to my poor grasp, touching on some provocative ideas.
Soundbloke's post leads to something I have pondered unsuccessfully for years: how to measure, depict, or hopefully, to quantify transient response.
First, the pronouncement of Earl is pretty much a dead-end because it is unhelpful as to "where to go from here" and seems to have assumptions that can't be easily evaluated or addressed in real-world audio testing... and doesn't lead to fixes because we can't fix our phases too well in multi-driver systems.
Long ago when studying motional feedback, I took automatically triggered Polaroid photos from a 'scope triggered by a mic*. Great "portraits" of the horrible auto output from pure Dirac pulse inputs, although made much better by MFB.
With AI, somebody could prolly quantify photos, eh? But that's just dreaming.
Any better ideas for quantifying transient response?**
B.
* anybody want to guess how many decades ago that was?
** relating that to human perception is the step beyond
Last edited:
I think we need to be careful here. The answer to the question in the OP (and the title of this thread) is a very definite "NO". You cannot know the transient (e.g. impulse) response given only the frequency response. As Earl mentions, you also need to know the phase response, since this tells you when each frequency component will appear in the time domain.
That is why this sentiment is not strictly correct:
What I think Ben is trying say is that it is the upper extent of the frequency response sets a lower bound regarding how fast a system can respond to a stimulus. That is true to the extent that a band-limited system can only respond as fast as its high frequency components will allow given the best possible phase response for the system.
But the converse is not always correct, e.g. that a system with flat and extended high frequency response MUST have good transient response. And the missing piece of relevant information is the phase response.
If you do some hand waving and say that the loudspeaker must be well-behaved and well-designed, yadda yadda then Ben's sentiment starts to ring true and we can make some educated guesses about what the phase response will look like.
So, to reiterate, if you only know the FR, then you cannot know for certain the time domain behavior. As an example, it's like the difference between two systems with the exact same FR, one of which can reproduce a square wave perfectly and the other is a jumbled mess in the time domain. It's very likely that these will sound exactly the same thanks to your ears+brain not being all that sensitive to "phase distortion" but they absolutely do not have the same time domain response.
That is why this sentiment is not strictly correct:
Invoking the term "mathematical truth" is just going to mislead the uninformed and, frankly, is anything but "truth".I think a way to look at that mathematical truth is that if the upper frequencies are present like with good tweeters, then the whole system reacts real quick... which is like saying the transient response is swell.
What I think Ben is trying say is that it is the upper extent of the frequency response sets a lower bound regarding how fast a system can respond to a stimulus. That is true to the extent that a band-limited system can only respond as fast as its high frequency components will allow given the best possible phase response for the system.
But the converse is not always correct, e.g. that a system with flat and extended high frequency response MUST have good transient response. And the missing piece of relevant information is the phase response.
If you do some hand waving and say that the loudspeaker must be well-behaved and well-designed, yadda yadda then Ben's sentiment starts to ring true and we can make some educated guesses about what the phase response will look like.
So, to reiterate, if you only know the FR, then you cannot know for certain the time domain behavior. As an example, it's like the difference between two systems with the exact same FR, one of which can reproduce a square wave perfectly and the other is a jumbled mess in the time domain. It's very likely that these will sound exactly the same thanks to your ears+brain not being all that sensitive to "phase distortion" but they absolutely do not have the same time domain response.
...What I think Ben is trying say is that it is the upper extent of the frequency response sets a lower bound regarding how fast a system can respond to a stimulus. That is true to the extent that a band-limited system can only respond as fast as its high frequency components will allow given the best possible phase response for the system.
Very helpful post. Further showing how unhelpful it can be to speak ideal math in the world of audio.
But there remains the question of real-world phase-skew and how much can materially effect transient perceptions. I wish Earl of somebody could benchmark the effect. Phase is all over the place on my REW room plots (which is rarely scan for lack of benefit doing so), but speakers sound like trumpets and drums.
Question: even with total phase alignment at the driver(s), wouldn't phase across the spectrum be wholly different (although orderly progressed) at your ear and again at the other ear?
BTW, do you mean "upper bound" rather than "lower bound"?
B.
Footnote: among the glories of my ESLs (and when I hear big Martin Logans at audio shows) is the marvellous transients. Seems to me that ESL technology bring advantages Rice-Kellogg drivers can't match.
Last edited:
I am sure that some limits could be established. But it might be more than what a "good and well designed loudspeaker" would exceed. It would be nice to know in any case.Very helpful post. Further showing how unhelpful it can be to speak ideal math in the world of audio.
But there remains the question of real-world phase-skew and how much can materially effect transient perceptions. I wish Earl of somebody could benchmark the effect. Phase is all over the place on my REW room plots (which is rarely scan for lack of benefit doing so), but speakers sound like trumpets and drums.
I meant lower bound in the sense that the response cannot get any faster, e.g. the time to respond any lower, than what the bandwidth of the system prescribes for a causal system. Here, by bandwidth, I essentially mean how high in frequency the system passband extends. Then, when there is additional phase rotation that causes more delay for higher frequencies, the response time will only get slower.BTW, do you mean "upper bound" rather than "lower bound"?
The bandwidth <--> transient response speed relationship is well known. You can make your driver "slower" just by adding a low pass filter that reduces its bandwidth by eliminating the high frequency part of the response.
I think we need to be careful here. The answer to the question in the OP (and the title of this thread) is a very definite "NO". You cannot know the transient (e.g. impulse) response given only the frequency response. As Earl mentions, you also need to know the phase response, since this tells you when each frequency component will appear in the time domain.
So, to reiterate, if you only know the FR, then you cannot know for certain the time domain behavior.
As this thread has been hot on technical accuracy, I will point out that the answer is a very definite "YES".
The frequency response as properly defined is complex and often represented as magnitude and phase responses. But from the complex frequency response (as opposed to just the magnitude response), the transient (meaning impulse) response/time domain behaviour is defined. They are just different representations of the same information.
Last edited:
This is, so far, the most civil and high-toned thread I can recall. And soundbloke seems, to my poor grasp, touching on some provocative ideas.
...
Any better ideas for quantifying transient response?**
Whilst the "civil" and "high-toned" labels are welcome, I would have hoped nothing I said was remotely "provocative". There is after all nothing new in my posts. Unfortunately depicting a complete characterisation of audible performance would likely take writing a book to answer - if indeed it could be done. Established theory has already filled large numbers of tomes, many of which are deeply mathematical and not exactly fun reading.
But if (as mentioned previously) we stick to the assumption of a linear system, then the two-dimensional time-frequency plane does offer a great insight into audible transient phenomena. The purest such representation from which to start is the Wigner Distribution (from which all other more common representations such as the cumulative attack/decay spectra emerge as windowed/filtered versions). Unfortunately there is no simple window/filter function (that I know) that suffices for characterising human hearing, but such a function would not likely be constant with time or frequency.
So after such a pretentious post, I will conclude by suggesting that developing a practical understanding of what the artefacts portrayed in (for example) a cumulative decay spectra add to the character of a speaker will endow you with the knowledge you seek. And things that ring are not what you seek...
True, though the amplitude and phase response (both in the frequency domain) are linked for minimum-phase systems, through the Hilbert transform. If you know one, you can calculate the other. Under some assumptions, subwoofers are minimum phase and so are their electronic crossovers.I think we need to be careful here. The answer to the question in the OP (and the title of this thread) is a very definite "NO". You cannot know the transient (e.g. impulse) response given only the frequency response. As Earl mentions, you also need to know the phase response, since this tells you when each frequency component will appear in the time domain.
So if you know ..
(1) the amplitude response
(2) the system is minimum-phase
.. then you can calculate (3) the phase response.
From (1) and (3), the impulse response can be calculated through the inverse Fourier transform.
Last edited:
True, though the amplitude and phase response (in the frequency domain) are linked for minimum-phase systems, through the Hilbert transform. If you know one, you can calculate the other. Subwoofers usually are minimum phase and so are their crossovers. Exceptions are FIR filters and crossovers in which multiple paths are summed (like acoustically in a multi way loudspeaker ..).
So if you know ..
(1) the amplitude response in the frequency domain
(2) the system is minimum-phase
.. then you can calculate (3) the phase response in the frequency domain.
From (1) and (3), the impulse response can be calculated.
Without wishing to sound ike a school teacher, this post has a number of technical errors...
Charlie Laub's post was not true because of his confusion of the terminology - which is a very common one.
Further and related to that...
The frequency response can be represented as a phase response and a magnitude response (not the amplitude response).
The amplitude response is the real part of the time response - which for us is the impulse response.
And whilst most drivers are minimum phase in their pass-bands when measured anechoically, the audible effects from their use in real loudspeakers in real rooms changes matters somewhat, although those matters can often be improved by departing from minimum phase - particularly in matters where fidelity in the time domain is important.
Like soundbloke, i also naturally think of frequency response as including phase, as being complex, being comprised of magnitude and phase vs frequency.
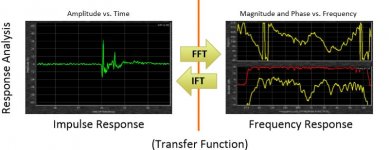
Which automatically brings mathematical equivalency between impulse response and frequency responses as per the chart below ( snipped from Rational Acoustic's manual).
The real beauty of this equivalency imo, is that perfectly flat magnitude and phase = a perfect impulse response, which = a dirac pulse, which also = perfect transient response.
An image of a dirac pulse that I've found very helpful in equating it to transient response goes like this.....
Take every frequency from 20Hz to 20kHz, or whatever you consider the audible range.
Simultaneously and instantly, produce every frequency.
That will mean the initial rise of every frequency's wave, starts at exactly the same time.
That is what perfectly flat mag and phase does.
It time aligns the initial start, the very first sample, of every frequency if simultaneously excited.
And its impulse response will be the summation of all those first samples, a dirac pulse.
So in the end, transient response simply equals FR response, phase included.
Hope that all made sense...
Which automatically brings mathematical equivalency between impulse response and frequency responses as per the chart below ( snipped from Rational Acoustic's manual).
The real beauty of this equivalency imo, is that perfectly flat magnitude and phase = a perfect impulse response, which = a dirac pulse, which also = perfect transient response.
An image of a dirac pulse that I've found very helpful in equating it to transient response goes like this.....
Take every frequency from 20Hz to 20kHz, or whatever you consider the audible range.
Simultaneously and instantly, produce every frequency.
That will mean the initial rise of every frequency's wave, starts at exactly the same time.
That is what perfectly flat mag and phase does.
It time aligns the initial start, the very first sample, of every frequency if simultaneously excited.
And its impulse response will be the summation of all those first samples, a dirac pulse.
So in the end, transient response simply equals FR response, phase included.
Hope that all made sense...
Attachments
Thanks for the correction 🙂The frequency response can be represented as a phase response and a magnitude response (not the amplitude response).
What other technical errors do you mean?
- Home
- Loudspeakers
- Subwoofers
- If I know the FR, do I know the transient response?