As Geddes has documented, reducing diffraction in a waveguide makes a significant improvement in the sound quality. I own a set of his Summas, and I find that the soundstage has greater depth, the speaker doesn't 'grate' on the ears the way a horn does, and the speaker just disappears.
Basically my Summas sound like a direct radiator, but with greater dynamics and a wider sweet spot.
Back in 2007 I made a mold for an oblate spheroidal waveguide, and it was a complete p.i.t.a. It took about a week to finish the mold, and it was not perfect.
In this thread I want to present a method of 'approximating' the OS curve, using parts you can buy at home depot. This method is basically identical to what Peavey did. (But Peavey didn't show you how to do it.)
Here's how you do it:
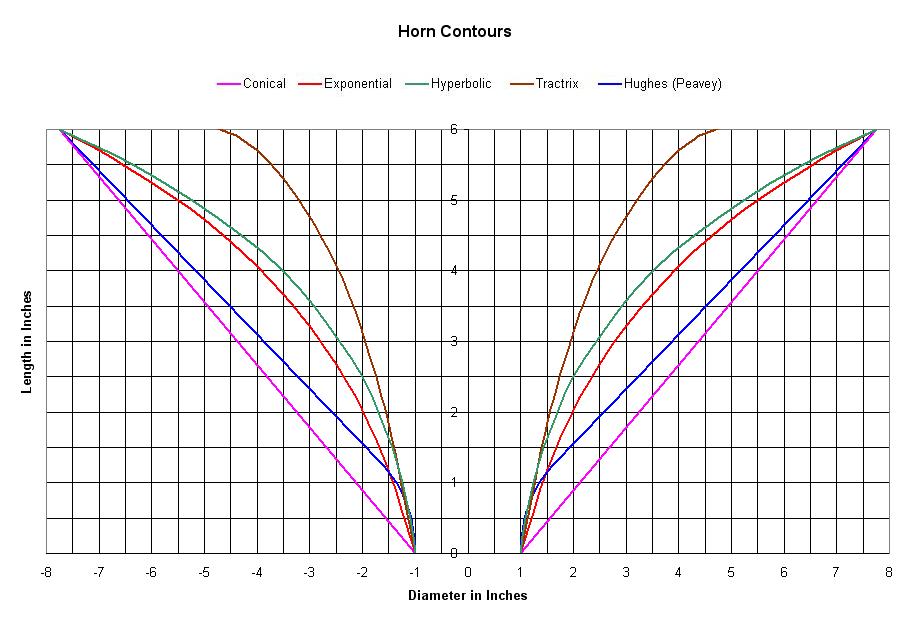
1) The difference between a conical horn and an oblate spheroidal waveguide is in the throat and the mouth. You can approximate the curve by using a roundover at the throat and at the mouth.
2) In order to approximate it, you build the horn in three segments : the body, the throat, and the mouth.
3) There are a dozen different ways to build the body of a conical horn. You can make it in 'petals' using Hornresp, or you could built it on a lathe.
4) The throat is possibly the trickiest. In my method, you build the throat up in layers. I have personally built horns and waveguides using molds and fiberglass, and I find that getting the throat perfectly circular is tricky with a mold. My 'new' method simply uses hole saws. By using a drill press and a hole saw you can insure that the throat is symmetrical and perfectly circular. This might seems like splitting hairs, but it's not; if the throat is off by even 20% it makes a measurable difference. And 20% is a tight tolerance for homemade waveguides, especially if you're construction is as sloppy as mine.

First, decide what the coverage angle is. And then drill four or five holes in wood or plastic that is 1/4" thick. The holes are 1", 1.125", 1.25", 1.5", and 2". A sixty degree waveguide only needs four layers (because it's narrower.)
Once you've drilled those holes, glue the layers together, then bond that mounting plate to the body of your horn. The mouth of the horn body will vary depending on your coverage angle. For a sixty degree waveguide it's 2", for 90 it's 2.5", and for 120 it's 3".
Again, this probably seems like a small thing, but it actually isn't. With a 90 degree conical horn there's a 1/2" difference between an oblate spheroidal waveguide and a conical horn. While one could get 'close' with a file and by doing it 'by eye', close isn't good enough; the throat of a waveguide or horn needs to be nearly perfect.
Once you've bonded your waveguide body to your throat, you'll still need sandpaper, bondo, and a file. But it will be much easier to keep everything symmetrical when you built the mounting plate using hole saws. Another benefit of this, which is the main reason that I am doing this, is that it's STRONG. I build a lot of Synergy horns and strength is important because of the low cutoff frequency.
Let me know if you have any questions.
Basically my Summas sound like a direct radiator, but with greater dynamics and a wider sweet spot.
Back in 2007 I made a mold for an oblate spheroidal waveguide, and it was a complete p.i.t.a. It took about a week to finish the mold, and it was not perfect.
In this thread I want to present a method of 'approximating' the OS curve, using parts you can buy at home depot. This method is basically identical to what Peavey did. (But Peavey didn't show you how to do it.)
Here's how you do it:
1) The difference between a conical horn and an oblate spheroidal waveguide is in the throat and the mouth. You can approximate the curve by using a roundover at the throat and at the mouth.
2) In order to approximate it, you build the horn in three segments : the body, the throat, and the mouth.
3) There are a dozen different ways to build the body of a conical horn. You can make it in 'petals' using Hornresp, or you could built it on a lathe.
4) The throat is possibly the trickiest. In my method, you build the throat up in layers. I have personally built horns and waveguides using molds and fiberglass, and I find that getting the throat perfectly circular is tricky with a mold. My 'new' method simply uses hole saws. By using a drill press and a hole saw you can insure that the throat is symmetrical and perfectly circular. This might seems like splitting hairs, but it's not; if the throat is off by even 20% it makes a measurable difference. And 20% is a tight tolerance for homemade waveguides, especially if you're construction is as sloppy as mine.

First, decide what the coverage angle is. And then drill four or five holes in wood or plastic that is 1/4" thick. The holes are 1", 1.125", 1.25", 1.5", and 2". A sixty degree waveguide only needs four layers (because it's narrower.)
Once you've drilled those holes, glue the layers together, then bond that mounting plate to the body of your horn. The mouth of the horn body will vary depending on your coverage angle. For a sixty degree waveguide it's 2", for 90 it's 2.5", and for 120 it's 3".
Again, this probably seems like a small thing, but it actually isn't. With a 90 degree conical horn there's a 1/2" difference between an oblate spheroidal waveguide and a conical horn. While one could get 'close' with a file and by doing it 'by eye', close isn't good enough; the throat of a waveguide or horn needs to be nearly perfect.
Once you've bonded your waveguide body to your throat, you'll still need sandpaper, bondo, and a file. But it will be much easier to keep everything symmetrical when you built the mounting plate using hole saws. Another benefit of this, which is the main reason that I am doing this, is that it's STRONG. I build a lot of Synergy horns and strength is important because of the low cutoff frequency.
Let me know if you have any questions.
Gotta be careful with the hole saws...rarely are they centered correctly on the bit which causes wobble, and the wobble causes the holes to be larger than what you planned and may not actually be perfectly round when you are done.
Horn Design & Construction Notes
Jigs/Tooling and Manufacturing Method:
1) Drill a pilot center hole in each piece (lamina, salami-slice)
2) Match-drill a set of radial holes in each piece (salami-slice) before drilling out the center. Make a jig for doing this. These sets of holes will be used for centering the pieces with dowel pins during assembly after the apertures in the center have been drilled out.
3) Use rotary broaches to drill-out the neck apertures. [1]
4) To form neck exterior, and the extents of body and mouth laminae, use a router and radius guide such as [2]
Math & Geometry:
The Horn of Freehafer [3], made popular by Geddes, is based on the Oblate Spheroidal Coordinate System [4]. Geometrically the horn is of infinite extent. When truncated, a detraction edge is presented to the outbound acoustic waves. To mitigate the attendant reflection of waves back down to the driver diaphragm, curved lips are added to form the horn mouth. The optimal shape of these is best approximated by a segment of Euler’s Spiral [5] (my conjecture).
Regards,
WHG
[1] Rotabroach® Annular Cutters
Rotabroach Annular Cutters for Mag Drills, Sheet Metal, and Industrial Applications
[2] Micro Fence Circle Jigs
Circle Jigs - Micro Fence - Precision tools for the discerning
Note: These tools will yield the precision required, but they are not cheap.
[3] Title: The Velocity Potential of a Hyperbolic Horn (Doctoral Dissertation)
Author: John Edwin Freehafer
B.S., Lehigh University 1931
M.S., Lehigh University 1933
P.H.D., Massachusetts Institute of Technology, 1937
[4] Oblate Spheroidal Coordinates
Oblate spheroidal coordinates - Wikipedia, the free encyclopedia
[5] Euler’s Spiral
Euler spiral - Wikipedia, the free encyclopedia
Jigs/Tooling and Manufacturing Method:
1) Drill a pilot center hole in each piece (lamina, salami-slice)
2) Match-drill a set of radial holes in each piece (salami-slice) before drilling out the center. Make a jig for doing this. These sets of holes will be used for centering the pieces with dowel pins during assembly after the apertures in the center have been drilled out.
3) Use rotary broaches to drill-out the neck apertures. [1]
4) To form neck exterior, and the extents of body and mouth laminae, use a router and radius guide such as [2]
Math & Geometry:
The Horn of Freehafer [3], made popular by Geddes, is based on the Oblate Spheroidal Coordinate System [4]. Geometrically the horn is of infinite extent. When truncated, a detraction edge is presented to the outbound acoustic waves. To mitigate the attendant reflection of waves back down to the driver diaphragm, curved lips are added to form the horn mouth. The optimal shape of these is best approximated by a segment of Euler’s Spiral [5] (my conjecture).
Regards,
WHG
[1] Rotabroach® Annular Cutters
Rotabroach Annular Cutters for Mag Drills, Sheet Metal, and Industrial Applications
[2] Micro Fence Circle Jigs
Circle Jigs - Micro Fence - Precision tools for the discerning
Note: These tools will yield the precision required, but they are not cheap.
[3] Title: The Velocity Potential of a Hyperbolic Horn (Doctoral Dissertation)
Author: John Edwin Freehafer
B.S., Lehigh University 1931
M.S., Lehigh University 1933
P.H.D., Massachusetts Institute of Technology, 1937
[4] Oblate Spheroidal Coordinates
Oblate spheroidal coordinates - Wikipedia, the free encyclopedia
[5] Euler’s Spiral
Euler spiral - Wikipedia, the free encyclopedia
Attachments
Last edited:
You could do it all with a hand router and a good circle jig. My the owner of my old shop would cut concentric rings out of various thicknesses of abs for fun...one of them was stacked with a dime on the inside, couldn't tell it was multiple pieces until you picked it up. Each ring was about 1/8th inch wide.

First segment of waveguide, using the guide from post #1






My inspiration was this QSC waveguide, which measures beautifully


wood filler helps a lot
Patrick, I very much appreciate and admire your experiments. Any follow up on this one?
I wonder what the final result looks like, with the walls smoothed and the roundovers.
By the way: what's your mathematical method to determine the segments of the roundover for the horizontal vs. the vertical sections of the mouth? There are simplified formulas to determine an Euler spiral (segment) for a given length and curvature without using the complex Fresnel integrals. I'll post these when/if I can dig them up.
I wonder what the final result looks like, with the walls smoothed and the roundovers.
By the way: what's your mathematical method to determine the segments of the roundover for the horizontal vs. the vertical sections of the mouth? There are simplified formulas to determine an Euler spiral (segment) for a given length and curvature without using the complex Fresnel integrals. I'll post these when/if I can dig them up.
- Status
- Not open for further replies.
- Home
- Loudspeakers
- Multi-Way
- How to Reduce Diffraction on Your Conical Horn