How to calculate the power of unknowm transformer?
SMPS ferrite transformer or 50hz laminatad iron transformer
You can't !
One can guess using a variety of rules, but they are VERY approximate.
One good rule, that used to be valid, that I still use is 3.1A/sqmm of copper. Now we see cheap overspecified toroids & EIs that use >4.5A/sqmm.
But Dini points out smps and in those I have seen as high as 12A/sqmm. They run HOT !
One can guess using a variety of rules, but they are VERY approximate.
One good rule, that used to be valid, that I still use is 3.1A/sqmm of copper. Now we see cheap overspecified toroids & EIs that use >4.5A/sqmm.
But Dini points out smps and in those I have seen as high as 12A/sqmm. They run HOT !
the thinner wire would be the higher voltage input/output and thicker wire would be lower voltage unless the difference is too small to notice or you cant actually see the wires.
I know where is input and output because is marked, it's and old power tx from Audionote DAC, I simulated with PSUDII and seems very low power 15mA for a resistive load of 22K.
Last edited:
try checking both input and output with 5-9V (reliable voltage and current) 100ohm resistor and check the current usage for a more accurate number. if you want to check voltage you might need to check the inductance of the input and output. check the voltage drop across the resistor as well. it might give suggestion to the transformer
Last edited:
Weigh it. Compare it with other transformers which appear to be of similar quality.
Run it into a power resistor. See how hot it gets. Snag is, you don't know how hot the insulation can get before failure. Generally, modern transformers can get hotter than older ones because modern insulation is better. This does not necessarily apply to cheap Chinese made ones, as they use newspaper for insulation - which is even worse than the high quality paper insulation in a 50-year-old western transformer.
Run it into a power resistor. See how hot it gets. Snag is, you don't know how hot the insulation can get before failure. Generally, modern transformers can get hotter than older ones because modern insulation is better. This does not necessarily apply to cheap Chinese made ones, as they use newspaper for insulation - which is even worse than the high quality paper insulation in a 50-year-old western transformer.
try checking both input and output with 5-9V (reliable voltage and current) 100ohm resistor and check the current usage for a more accurate number. if you want to check voltage you might need to check the inductance of the input and output. check the voltage drop across the resistor as well. it might give suggestion to the transformer
5-9V AC?
100R 1/2W is enough?
just simple
download (Transformer calculator)
http://www.sklaic.info/download.php?id=trcal01
then
https://www.flickr.com/photos/33267726@N06/25010534613/in/dateposted-public/
download (Transformer calculator)
http://www.sklaic.info/download.php?id=trcal01
then
https://www.flickr.com/photos/33267726@N06/25010534613/in/dateposted-public/
Like a transformer designer would 😛How to calculate the power of unknowm transformer?
Given everything else stays the same (transformer core material, wire current density, etc.), Power , or more precisely VA is directly proportional to the square of core area .
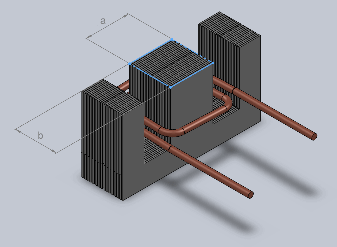
Core area S is A*B in square centimeters.
For average silicon steel laminations (what 95% of makers use) and average current density (about 3A/mm^2 seems to be a standard these days) , basic power calculation is:
P(VA)=k*S^2
for good laminations and a commercial design (meaning cost and performance must be balanced) k can be as low as 1
If cheap laminations (below average) are used, then k will be less, meaning less power available.
Examples:
a) Regular modern transformer, bought from a reputable supplier , those which can be left plugged to mains, no load on the secondary, get only warm after 1 hour, k~1 , 25mm * 25mm core:
(2.5 cm * 2.5 cm)^2=6.25^2=39VA
b) same but "mystery maker" , "special offer" , etc., those which even if unloaded become quite hot to the touch (meaning tuna can quality iron)
Same Math but k~0.8 meaning you should demand no more than ~30VA from it.
c) if amplifier $$$ justifies it, the transformer may be wound with thick wire (current density ~2A/mm^2) , on next larger lamination (mainly to increase window size for all that copper) and user higher quality (less lossy) steel.
Will be quite more expensive, of course.
Dimensions are easy to measure:
B is directly measurable, it's lamination "stack" thickness.
A is sometimes harder or hidden by the wire bobbin, but in standard transformers it's usually 1/3 the length of the lamination, so the 25mm wide core corresponds to 75mm lamination.
Many shapes and proportions are possible, depending on purpose, but most efficient way to punch/cut a sheet of silicon steel to make EI laminations is the so called "scrapless" shape, really NO scrap lost, and there core is 1/3 the external size which is easy to measure.

Aren't transformer voltage ratings at their rated current. I.e. apply a load on the secondary winding until you see 20v out, there is your approx amperage rating for that winding?
No. Voltages are nominal. You can't assume a "20V" winding will deliver exactly 20V when correctly loaded. Also, if there are other secondaries they must also be loaded. Primary voltage matters too.
Like a transformer designer would 😛
Given everything else stays the same (transformer core material, wire current density, etc.), Power , or more precisely VA is directly proportional to the square of core area.
Core area S is A*B in square centimeters.
For average silicon steel laminations (what 95% of makers use) and average current density (about 3A/mm² seems to be a standard these days) , basic power calculation is:
P(VA)=k*S²
Hmmm… I'm going to confess early on: of magnetics I know not much beyond what I remember from UC physics 1. (Which is to say, not much!)
But I kind of thought that VA scaling would have to scale linearly with the mass of energized iron. (Which comes directly from the idea that magnetic energization of the core material (and free space, were it not there) is the coupling between windings.)
The proxy for energized mass (represented by 'k' in your great comment) is “a” and “b” and “c” the other dimension. All things equal (and when does that happen? HAH!) if a formula for some transformer is:
a = b = 1 and c = 10 (in same units as a, b) then a transformer having
a = b = 2 would most likely have c = 20.
Linear scaling of dimensions “in the formula”. But that also implies:
a² • b² • c² = 100 in the first case and
a² • b² • c² = 6400 in the 'twice as large but scaled' case.
or as your point is:
a² • b² = 1.0 in the first case and
a² • b² = 16.0 in the 'twice as large but scaled' case.
Dunno… I'd have a hard time accepting that a transformer that has 8× the mass (2 times the size of all dimensions doubled) is going to handle 16× the power. But who knows, with scaling efficiencies (for larger cores entraining more magnetic field)... could be!
___
Meanwhile … GoatGuy goes on a Hammond Industrial foray
http://www.hammondpowersolutions.com/files/HPS_Catalogue_Transformer_Products_Web_Version.pdf
___
So, using their open-frame transformers on page 45, 46 and so on, and using the factors known as "A" (core width), "C" (core height) and "E - 0.5" (est core depth), and Hammond's VA ratings, I did this:
PSF = VA / (A • B • (E - 0.5)) for the 50 thru 5,000 VA series
Here are the results (PSF = power scaling factor):
VA 50, vol 11.8, PSF 4.21
VA 100, vol 15, PSF 6.63
VA 150, vol 19, PSF 7.88
VA 250, vol 28, PSF 8.92
VA 350, vol 32.5, PSF 10.7
VA 500, vol 45.1, PSF 11
VA 750, vol 70, PSF 10.7
VA 1000, vol 77.6, PSF 12.8
VA 1500, vol 104, PSF 14.3
VA 2000, vol 132, PSF 15
VA 3000, vol 260, PSF 11.5
VA 5000, vol 380, PSF 13.1
If the scaling were (a² • b²) as you pointed out, then I'd have expected that the PSF would have scaled by volume to the ⁴/₃ power ( cube root or ⅓ power normalizes volume to an abstract single factor, then raised to the fourth power delivers the a²b² idea.)
Actually, I can't tell from eyeballing. Looks like the VA 350 to 5000 bunch have a PSF of about 12 “VA per core volume", on the average, with no particular trend apparent. When I normalized the volume (off the littlest one) by the ⁴/₃ power, the PSF table became:
VA 50 , vol₄₃ 11.8 PSF₄₃ 4.21
VA 100 , vol₄₃ 16.3 PSF₄₃ 6.11
VA 150 , vol₄₃ 22.2 PSF₄₃ 6.73
VA 250 , vol₄₃ 37.3 PSF₄₃ 6.69
VA 350 , vol₄₃ 45.5 PSF₄₃ 7.68
VA 500 , vol43 70.5 PSF₄₃ 7.09
VA 750 , vol₄₃ 126 PSF₄₃ 5.92
VA 1000 , vol₄₃ 145 PSF₄₃ 6.87
VA 1500 , vol43 216 PSF₄₃ 6.92
VA 2000 , vol₄₃ 296 PSF₄₃ 6.74
VA 3000 , vol₄₃ 727 PSF₄₃ 4.12
VA 5000 , vol43 1,210 PSF₄₃ 4.13
Which appears to be a better fit … and confirming what you said. Except it kind of isn't. There's a peak in the middle, and a droop as transformer VA ratings get larger.
Well … now I don't know what to think.
GoatGuy
Last edited:
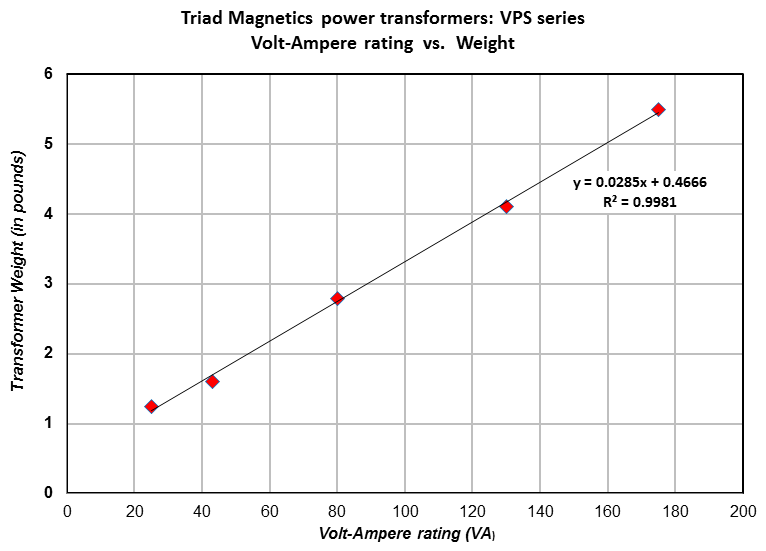
Here is an example using a few datapoints from the VPS series of transformers made by Triad. VA ratings and weights copied straight from Triad's website. Notice the Rsquared (goodness of fit) coefficient.Weigh it. Compare it with other transformers which appear to be of similar quality.
_
So If I have a small open EI trafo 120 Input, secondaries 52VCT with ~18mmx18mm core (dimension of core is 50x42x18mm) I get about 10VA with Jim Faheys guesstimate. It appears to be about the same size as a marked 15VA transformer, so it seems reasonable.
PAFis estimate using the above 10VA and a coil winding resistance of 34ohms gives something like 0.34A primary current. Is this more a number for sizing fuses, or ?
Is there a test regime that can roughly reveal the SOA of a transformer based on voltage drop with increasing load at the secondary and/or equilibrium temperature?
PAFis estimate using the above 10VA and a coil winding resistance of 34ohms gives something like 0.34A primary current. Is this more a number for sizing fuses, or ?
Is there a test regime that can roughly reveal the SOA of a transformer based on voltage drop with increasing load at the secondary and/or equilibrium temperature?
- Status
- Not open for further replies.
- Home
- Amplifiers
- Power Supplies
- How to calculate power of unknowm transformer
