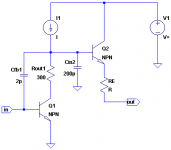
Hi friends please help me on this...
I want to know how exactly modifying the value of Cfb1 in the circuit raises the second pole to a higher frequency..
As the circuit involves two poles...
The first pole is due to the feedback capacitance and the second pole is due to Rout1 and Cin2..
now since increase in value of Cfb1 increases the negative feedback which decreases the gain and the output resistance (Rout1) of the first stage, which further increases the second pole to a higher value ..much higher in frequency...
So how does decrease in the value of Rout1 due to Cfb1 shift the second pole to a higher frequency...
I need some intuitive explanation....
Thanks!!
source:Music and Audio Electronics
I want to know how exactly modifying the value of Cfb1 in the circuit raises the second pole to a higher frequency..
As the circuit involves two poles...
The first pole is due to the feedback capacitance and the second pole is due to Rout1 and Cin2..
now since increase in value of Cfb1 increases the negative feedback which decreases the gain and the output resistance (Rout1) of the first stage, which further increases the second pole to a higher value ..much higher in frequency...
So how does decrease in the value of Rout1 due to Cfb1 shift the second pole to a higher frequency...
I need some intuitive explanation....
Thanks!!
source:Music and Audio Electronics
Attachments
You understand it wrongly. We add Cfb1 (on purpose) into the circuit in order to pole splitting occurred. Without Cfb1 pole splitting does not occur.
The pole due to Cfb1 does not shift to a higher frequency. It becomes lower - a lot lower and becomes the single dominant pole. Hence pole splitting - one goes way down the others go way up. You sacrifice one that you can control to effectively remove the ones you can't. Those other non-dominant poles are often ill-defined - they depend heavily on output stage bias, output voltage, output/driver transistor beta (which isn't constant),and load (which is highly complex).
What I know is this....
Since Rout decreases with increase in value of Cfb1.....and this reduced high-frequency output impedance resulting from this moves the second pole (associated with second stage input) up.
But can someone tell me how exactly does it happens...
Is Rout1 and Cin2 is acting as a filter....or something like that..??
Since Rout decreases with increase in value of Cfb1.....and this reduced high-frequency output impedance resulting from this moves the second pole (associated with second stage input) up.
But can someone tell me how exactly does it happens...
Is Rout1 and Cin2 is acting as a filter....or something like that..??
Yes, Rou1 and Cin2 form a low pass filter.But can someone tell me how exactly does it happens...
Is Rout1 and Cin2 is acting as a filter....or something like that..??
p2 =1/(Rou2 * Cin2)
Also do you understand the feedback theory? And why Rout1 decreases when we apply a negative (voltage)feedback?
The situation looks like this:
Without the feedback Rout1 = Rout1, but as we add an negative feedback across the amplifier the Rout1 will decreases to the new value
Rou1 = Rout1/(1 + |Av|) this is true for the case of an infinitely large feedback capacitor Cfb1.
The time constant associated with Cin2 therefore changes by a similar ratio, moving to higher frequency as the feedback capacitor (Cfb1) increases.
In the limit of very large Av and Cfb1, the output resistance approaches Rou1/|Av|. Furthermore the output (Cin2) and input capacitors (not present here) are essentially shorted together in that limit, leading to an output pole of p2 = 1/[(Rou1*Cin2)/|Av|].
But we already discussed this on the other forum.
Last edited:
Well you mean that Rout1 decreases by a factor of 1/(1 + |Av|) as the value of feedback cap Cfb1 increases...as the time constant is the product of Rout1 and Cin2 which means that if Rout decreases by a factor it means that Cin2 will also decrease by the same factor i.e by 1/(1 + |Av|) and as f2 inverse prop to (Rout1 * Cin2) means that the second pole is shifted to much higher frequency..right??
According to your formula p2 = 1/[(Rout1*Cin2)/|Av|] means that if more the Av increases the second pole will move much higher in frequency ..ok
and for Av to be high Cfb1 should be less..and that means that the lesser the Cfb1 is the more pole splits apart...but how this can be possible as the text say opposite of this is true..i.e the phenomenon of pole splitting occurs when the value of Cfb1 increases...
please clarify??
and for Av to be high Cfb1 should be less..and that means that the lesser the Cfb1 is the more pole splits apart...but how this can be possible as the text say opposite of this is true..i.e the phenomenon of pole splitting occurs when the value of Cfb1 increases...
please clarify??
You got that rightWell you mean that Rout1 decreases by a factor of 1/(1 + |Av|) as the value of feedback cap Cfb1 increases...as the time constant is the product of Rout1 and Cin2 which means that if Rout decreases by a factor it means that Cin2 will also decrease by the same factor i.e by 1/(1 + |Av|) and as f2 inverse prop to (Rout1 * Cin2) means that the second pole is shifted to much higher frequency..right??
No wrong. This equation is true only when we have a large negative feedback (Cfb1 is large). But for small Cfb1 feedback is too weak.According to your formula p2 = 1/[(Rout1*Cin2)/|Av|] means that if more the Av increases the second pole will move much higher in frequency ..ok
and for Av to be high Cfb1 should be less..and that means that the lesser the Cfb1 is the more pole splits apart...but how this can be possible as the text say opposite of this is true..i.e the phenomenon of pole splitting occurs when the value of Cfb1 increases...
please clarify??
If you want to analysis the full expression without large number of approximations that fine with me. But good luck for you if you will see any intuitive inside. Try read jcx link.
But I am still not getting this...it just simple maths..p2 = 1/[(Rout1*Cin2)/|Av|]
with large negative feedback Av decreases...and if Av decreases the whole denominator
term (Rout1*Cin2)/|Av|) increases ..and if it increases p2 automatically decreases...
so how does it seems relevant that With Large Cfb1 and large Av p2 decreases..
but as it should be with low Cfb1 and large Av ..then p2 increases?
But yet again its going against my conclusion in post 9 first part....
I am confused??
with large negative feedback Av decreases...and if Av decreases the whole denominator
term (Rout1*Cin2)/|Av|) increases ..and if it increases p2 automatically decreases...
so how does it seems relevant that With Large Cfb1 and large Av p2 decreases..
but as it should be with low Cfb1 and large Av ..then p2 increases?
But yet again its going against my conclusion in post 9 first part....
I am confused??
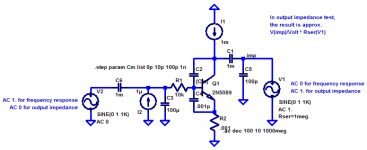
Here's something to play around with in LTspice. It's the first stage, with a capacitor simulating second-stage input impedance (and giving the resulting second pole).
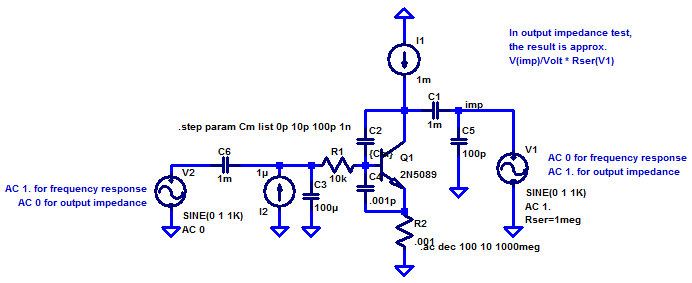
You can see how the first pole (associated with the transition from constant high impedance to first-order dropoff at low frequencies) is shifted to the left as Cm is increased. The second pole is associated with the dropoff after the second, higher-frequency shelf, and that gets shifted to the right as the impedance shelf moves down.
You can see how the first pole (associated with the transition from constant high impedance to first-order dropoff at low frequencies) is shifted to the left as Cm is increased. The second pole is associated with the dropoff after the second, higher-frequency shelf, and that gets shifted to the right as the impedance shelf moves down.
Attachments
- Status
- Not open for further replies.
- Home
- Amplifiers
- Solid State
- How does pole splitting works ?