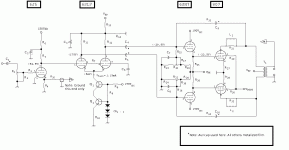
How do I calculate the feedback % for a simple 1 resistor plate to grid (schade style) feedback loop? (I'm looking at various 807 amp schematics, and I've seen 70k to 200k being used between the 807 plate and driver plate(807 grid).
In the Schade paper, he uses a voltage divider w/ two resistors, and that going to a transformer, and I understand how he gets his 10% there.
But, w/ just one resistor.... I'm not sure how to figure it out...
Thanks for any help.
In the Schade paper, he uses a voltage divider w/ two resistors, and that going to a transformer, and I understand how he gets his 10% there.
But, w/ just one resistor.... I'm not sure how to figure it out...
Thanks for any help.
With just one resistor, you can't figure it out. As jazbo8 says, you need to include the output impedance of the previous stage. Then you have two resistances and you can form a ratio.
Edit,
My answer didn't make sense, but Rs for the previous stage, not the output stage? I was calculating the values for the output stage
(so using my output tx as Ra, etc).
My answer didn't make sense, but Rs for the previous stage, not the output stage? I was calculating the values for the output stage
(so using my output tx as Ra, etc).
Last edited:
You do have two resistances there that form a voltage divider. From the schemo of the Vixen, R33 and R34 connect to the node at the control grid of the 6SN7 cathode follower.
There, you have three impedances in parallel: the 1M DC grid return resistance, the plate load of the 6SL7 LTP (220K) and the rp of the 6SL7. From the loadline of the 6SL7, rp= 73.8K which agrees closely with the 74K plate resistance from the plate characteristic graph at the design plate current. Therefore:
G`= 1/1E6 + 1/220E3 + 1/74E3= 19.06uA/V
R`= 1/G`= 52.47K
Since you want 10% feedabck as Schade recommended, you need:
Rf= 9 X R`= 472.22K
Select: Rf= 470K (design nominal) and done.
There, you have three impedances in parallel: the 1M DC grid return resistance, the plate load of the 6SL7 LTP (220K) and the rp of the 6SL7. From the loadline of the 6SL7, rp= 73.8K which agrees closely with the 74K plate resistance from the plate characteristic graph at the design plate current. Therefore:
G`= 1/1E6 + 1/220E3 + 1/74E3= 19.06uA/V
R`= 1/G`= 52.47K
Since you want 10% feedabck as Schade recommended, you need:
Rf= 9 X R`= 472.22K
Select: Rf= 470K (design nominal) and done.
Attachments
I think so. If Rk is not bypassed (as in the case of the RH amplifiers), then Rs would need to be modified to Rp//Rg//(rp+(1+u)*Rk).Is that right? (help...)
Uh oh...
I goofed up the first workthrough, and I didn't catch it until I worked through both methods. Maybe one of the moderators can delete my first, goofed-up workthrough post? That's post #5 in this thread.
I figured it out.... My bad! In the first workthrough, I goofed up the zeros. I left out three zeros at one step, and came out with 8152 when I should have come out with 8,152,000. Big difference! The first method gave me Rfb of about 500k, the second 423k. Pretty close, since I'd probably grab a 470k resistor from stock anyway.
Thanks!
--
I goofed up the first workthrough, and I didn't catch it until I worked through both methods. Maybe one of the moderators can delete my first, goofed-up workthrough post? That's post #5 in this thread.
I figured it out.... My bad! In the first workthrough, I goofed up the zeros. I left out three zeros at one step, and came out with 8152 when I should have come out with 8,152,000. Big difference! The first method gave me Rfb of about 500k, the second 423k. Pretty close, since I'd probably grab a 470k resistor from stock anyway.
Thanks!
--
Last edited:
I'm still not getting the same result for Rfb from Miles' and Jazbo's methods. Or, as is very possible, I'm not doing it right.
I just pulled up Schade's paper. In fig. 33c (page 360), it shows a practical push-pull circuit with a transformer coupled input. For an example, it shows the 6L6 Rg as 10k, Rfb as 90k, with Rfb being 9X the value of Rg.
I know the Ra//ra of the previous stage will be in parallel with the 6L6's Rg, so correcting for that I'd see Ra//ra//Rg. Call that Rs.
So then, Rfb should be about 9X the value of Rs?
If I do it that way, then
250k * 75k * 250k = 4,687,500k
250k + 75k + 250k = 575k
4,687,500k / 575k = 8,152k
Rs / Rs+Rfb = beta (feedback factor)
If Rfb = 430k,
8152k / 8152k + 430k = 0.95
Argh. I think I'm misunderstanding how to apply the value of beta to this.
--
I just pulled up Schade's paper. In fig. 33c (page 360), it shows a practical push-pull circuit with a transformer coupled input. For an example, it shows the 6L6 Rg as 10k, Rfb as 90k, with Rfb being 9X the value of Rg.
I know the Ra//ra of the previous stage will be in parallel with the 6L6's Rg, so correcting for that I'd see Ra//ra//Rg. Call that Rs.
So then, Rfb should be about 9X the value of Rs?
If I do it that way, then
250k * 75k * 250k = 4,687,500k
250k + 75k + 250k = 575k
4,687,500k / 575k = 8,152k
Rs / Rs+Rfb = beta (feedback factor)
If Rfb = 430k,
8152k / 8152k + 430k = 0.95
Argh. I think I'm misunderstanding how to apply the value of beta to this.
--
Last edited:
I goofed up the first workthrough, and I didn't catch it until I worked through both methods. Maybe one of the moderators can delete my first, goofed-up workthrough post? That's post #5 in this thread.
<snip>
--
Done! 😀
Something went haywire with the above calculations...If I do it that way, then
250k * 75k * 250k = 4,687,500k
250k + 75k + 250k = 575k
4,687,500k / 575k = 8,152k
Rs = 250k//75k//250k = 46.875k, so if you want 10% LNFB, then Rfb = 9* 46.875k = 421.875k
You can get the parallel equivalent of two resistors by putting the product over the sum. It doesn't work for three resistors; the dimensions are wrong ([ohm^3]/[ohm] = [ohm^2]). For three resistors you have to divide the product by the sum of pairs of products (I think).
Well, thanks for that.
I went and looked it up, and I did have it all goofed up. What's really embarrassing is that I used to know this, but forgot. Ay yi yi.
For dissimilar value resistors in parallel:
1 / 1/R1 + 1/R2 + 1/R3...
So I tried it with 250k//250k//75k, and guess what?
I get 46,875
😱
(How's that for looking dumb in public...)
--
I went and looked it up, and I did have it all goofed up. What's really embarrassing is that I used to know this, but forgot. Ay yi yi.
For dissimilar value resistors in parallel:
1 / 1/R1 + 1/R2 + 1/R3...
So I tried it with 250k//250k//75k, and guess what?
I get 46,875
😱
(How's that for looking dumb in public...)
--
How do I calculate the feedback % for a simple 1 resistor plate to grid (schade style) feedback loop? (I'm looking at various 807 amp schematics, and I've seen 70k to 200k being used between the 807 plate and driver plate(807 grid).
In the Schade paper, he uses a voltage divider w/ two resistors, and that going to a transformer, and I understand how he gets his 10% there.
But, w/ just one resistor.... I'm not sure how to figure it out...
Thanks for any help.
A question - do you have perchance a link to that Schade paper?
TIA,
Jan
A question - do you have perchance a link to that Schade paper?
TIA,
Jan
It's on Pete's site: Beam Power Tubes
- Status
- Not open for further replies.
- Home
- Amplifiers
- Tubes / Valves
- How do I calculate local feedback %?