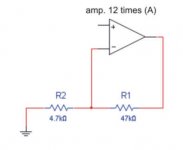
EchoWars said:Gain(db) = 20(log A)
A = simple voltage gain.
Your example = 21.6db
This is the open loop gain of A. I guess he wants the gain with the feedback loop closed, as shown?
[Hint: it is NOT 20 log (47k+4.7K/ 4.7k)]
Jan Didden
This is wrong?
An externally hosted image should be here but it was not working when we last tested it.
EchoWars said:This is wrong?
An externally hosted image should be here but it was not working when we last tested it.
This is an approximation, assuming that the gain of the amp block is (very) much higher than 1/beta. I understood from the first post that the amp block open loop gain was 12?
Edit: Beta of course being the feedback network attenuation
Jan Didden
Progg70 said:OK!?
So what is the right formula to get the feedback Db?
Hi Progg70,
Can you be a bit more specific? What exactly do you want? The gain of the amp? Closed loop, open loop? The gain of the feedback network itself? The gain of 12 you showed, what is that? The gain block, or the complete closed loop amp circuit? And if the latter, it's wrong.
Please think a moment and then formulate your question.
Jan Didden
I believe he's wanting you to assume that he's working with an opamp here (OLG very large).
It's what I assumed until I saw what you were getting at.
It's what I assumed until I saw what you were getting at.
Progg70 said:What is the formula to calculate feedback in Db?
20Log (loop-gain)
=
20log(feedback fraction*foward-path gain)
Note that loop-gain (and therefore stability or lack thereof) for the non-inverting and the inverting arrangements is identical.
EchoWars said:I believe he's wanting you to assume that he's working with an opamp here (OLG very large).
It's what I assumed until I saw what you were getting at.
Yeah. It was the "gain = 12" that got me wondering what that was. I assumed it was the gain block gain. Now I realised he may have meant the total circuit gain, but then the 12 is wrong of course.
Jan Didden
My attempt
If the amplifier voltage gain is A and the feedback attenuation is B
The closed loop gain X = A / [ 1 + (A x B )]
The feedback factor is Y = A / X
The feedback factor in decibels = 20 x log( Y )
[note: this is base 10 log not natural log]
In your diagram, B = R2 / (R1 + R2)
Remember that in a real life amp A changes with frequency and the input impedance of the amp may alter the effective value of B. Any load on the amp output may also change the effective value of A.
If the amplifier voltage gain is A and the feedback attenuation is B
The closed loop gain X = A / [ 1 + (A x B )]
The feedback factor is Y = A / X
The feedback factor in decibels = 20 x log( Y )
[note: this is base 10 log not natural log]
In your diagram, B = R2 / (R1 + R2)
Remember that in a real life amp A changes with frequency and the input impedance of the amp may alter the effective value of B. Any load on the amp output may also change the effective value of A.
Re: My attempt
Incorrect i fear. You've mistaken the return difference (1+(A*b)) for the amount of feedback, which i described here.
traderbam said:If the amplifier voltage gain is A and the feedback attenuation is B
The closed loop gain X = A / [ 1 + (A x B )]
The feedback factor is Y = A / X
The feedback factor in decibels = 20 x log( Y )
[note: this is base 10 log not natural log]
In your diagram, B = R2 / (R1 + R2)
Remember that in a real life amp A changes with frequency and the input impedance of the amp may alter the effective value of B. Any load on the amp output may also change the effective value of A.
Incorrect i fear. You've mistaken the return difference (1+(A*b)) for the amount of feedback, which i described here.
Hi,
have we sorted out what the 12 represented?
If open loop gain =12 =+21.58db
closed loop gain~=47/4.7+1=11=+20.83db. This is approximate because the accurate formula is quite complicated, particularly appropriate as closed loop gain approaches open loop gain.
feedback ratio is open loop gain - closed loop gain =21.58-20.83=0.75db. Hardly worth closing the loop, since all the advantages of closing the loop are proportional to the magnitude of the feedback factor.
The accurate formula for closed loop gain of an inverting amp is
Av=Rfb/[Rg+(Rfb+Rg)/A] where Rfb=the feedback resistor (47k)
Rg=lower leg resistor to common (4k7), A = open loop gain (x12)
what is the correction factor when non inverting is being used?
Just to check my arithmetic, I think the corrected closed loop gain is 5.22 (+14.35db) resulting in a feedback factor of 7.2db.
Am I close? or is it 6.22?
have we sorted out what the 12 represented?
If open loop gain =12 =+21.58db
closed loop gain~=47/4.7+1=11=+20.83db. This is approximate because the accurate formula is quite complicated, particularly appropriate as closed loop gain approaches open loop gain.
feedback ratio is open loop gain - closed loop gain =21.58-20.83=0.75db. Hardly worth closing the loop, since all the advantages of closing the loop are proportional to the magnitude of the feedback factor.
The accurate formula for closed loop gain of an inverting amp is
Av=Rfb/[Rg+(Rfb+Rg)/A] where Rfb=the feedback resistor (47k)
Rg=lower leg resistor to common (4k7), A = open loop gain (x12)
what is the correction factor when non inverting is being used?
Just to check my arithmetic, I think the corrected closed loop gain is 5.22 (+14.35db) resulting in a feedback factor of 7.2db.
Am I close? or is it 6.22?
Hi Andrew:
It's a universal formula.
A must be greater than B in order for the circuit drawn in my picture to work as an amplifier instead of a mere oscillator. A is thus always greater than 1 whereas B is between 0 and 1.
Regards,
Milan
It's a universal formula.
A must be greater than B in order for the circuit drawn in my picture to work as an amplifier instead of a mere oscillator. A is thus always greater than 1 whereas B is between 0 and 1.
Regards,
Milan
- Status
- Not open for further replies.
- Home
- Amplifiers
- Solid State
- Formula for calculate feedback in Db