I've built a DRD 300B decade ago and the amp is in the closet.
Electra-Print.com 300B DRD Audio Tube Amplifier
Recently, I saw a post about using Emission Labs 300B Mesh by not exceeding its limitation of 22W plate dissipation.
I'm curious how the DRD 300B adopt this meah tube in the circuit with operating point: 350v @63mA??
Electra-Print.com 300B DRD Audio Tube Amplifier
Recently, I saw a post about using Emission Labs 300B Mesh by not exceeding its limitation of 22W plate dissipation.
I'm curious how the DRD 300B adopt this meah tube in the circuit with operating point: 350v @63mA??
nicoch58,
I always find these figures for output power to be optimistic for what someone would accept for good sound in a music system.
A guitar amp can be different, though.
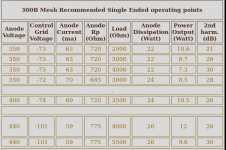
From the table:
350V, 63mA, 2000 Ohm load, 10.6 Watts, -21dB 2nd harmonic.
-21 dB 2nd harmonic is 8.9% distortion, but it does not include the 3rd harmonic distortion.
If the 300B current swings from 63mA to 126mA, (and in the other direction to 0 mA), the power is:
(Isquared * R)/2
The 2 comes from the fact that you want the rms power, not the peak power.
63mA change is the peak current change.
(0.063 squared * 2000)/2 = 3.97 Watts rms, or 7.94 Watts peak.
Of course, 0mA is clipping, and the peak current will be more than 2X 63mA.
But those current level extremes are all distortion, not the original signal.
So yes, you can have 10.6 Watts, but at more than 8.9 % THD (Total Harmonic Distortion).
For a real amplifier, the power will be less than that, because of the insertion loss of the output transformer.
Example, a transformer with 0.5 dB insertion loss will only have 0.89 times the calculated power from the tube.
3.97 Watts * 0.89 = 3.54 Watts.
Accept lower power, more distortion, or change the circuit and/or parts.
I always find these figures for output power to be optimistic for what someone would accept for good sound in a music system.
A guitar amp can be different, though.
From the table:
350V, 63mA, 2000 Ohm load, 10.6 Watts, -21dB 2nd harmonic.
-21 dB 2nd harmonic is 8.9% distortion, but it does not include the 3rd harmonic distortion.
If the 300B current swings from 63mA to 126mA, (and in the other direction to 0 mA), the power is:
(Isquared * R)/2
The 2 comes from the fact that you want the rms power, not the peak power.
63mA change is the peak current change.
(0.063 squared * 2000)/2 = 3.97 Watts rms, or 7.94 Watts peak.
Of course, 0mA is clipping, and the peak current will be more than 2X 63mA.
But those current level extremes are all distortion, not the original signal.
So yes, you can have 10.6 Watts, but at more than 8.9 % THD (Total Harmonic Distortion).
For a real amplifier, the power will be less than that, because of the insertion loss of the output transformer.
Example, a transformer with 0.5 dB insertion loss will only have 0.89 times the calculated power from the tube.
3.97 Watts * 0.89 = 3.54 Watts.
Accept lower power, more distortion, or change the circuit and/or parts.
Last edited:
The peak voltage of a pure (undistorted) sine wave is Root(2) times higher than the rms voltage of that same sine wave.
Root(2) = 1.414 to 4 place accuracy.
Peak = 1.414 x rms.
A 10Volt rms pure sine wave has 14.14V peak at the crest.
The rms voltage of a pure sine wave is 0.707 times the peak voltage at the crest of the sine wave.
peak voltage x 0.707 rms voltage.
A 10V peak sine wave is 7.07V rms.
Power = (E)squared/R, where power is rms, E is voltage rms, and the signal is a pure sine wave.
But since the peak of a pure sine wave is 1.414 times the rms, then the peak power is:
1.414 x 1.414 x rms power. 1.414 x 1.414 = 1.999 to 4 places (after all, 1.414 came from Root(2)).
2 x rms power = peak power.
Root(2) = 1.414 to 4 place accuracy.
Peak = 1.414 x rms.
A 10Volt rms pure sine wave has 14.14V peak at the crest.
The rms voltage of a pure sine wave is 0.707 times the peak voltage at the crest of the sine wave.
peak voltage x 0.707 rms voltage.
A 10V peak sine wave is 7.07V rms.
Power = (E)squared/R, where power is rms, E is voltage rms, and the signal is a pure sine wave.
But since the peak of a pure sine wave is 1.414 times the rms, then the peak power is:
1.414 x 1.414 x rms power. 1.414 x 1.414 = 1.999 to 4 places (after all, 1.414 came from Root(2)).
2 x rms power = peak power.
disco,
Your formula is correct.
Consider an 8V peak to peak sine wave.
Yes, that is 2.828Vrms. That is 1 Watt rms into 8 Ohms.
But, it is 2 Watts peak into 8 Ohms.
Now, consider an 8V peak to peak square wave.
That is 4Vrms. That is 2 Watts rms into 8 Ohms.
And it is 2 watts peak into 8 Ohms.
Consider a 500 Hz sine wave that is 4 Volts peak to peak.
Consider a 700 Hz sine wave that is 4 Volts peak to peak.
Turn either tone on, and get 4 Volts peak to peak.
Turn both tones on, and get 8 Volts peak to peak.
You will get less than 1 Watt rms into 8 Ohms on a true power meter.
The peak power is 2 Watts.
The point is, the sine wave, square wave, and the two tones all have 8V peak to peak.
Each of them has a Different rms power.
But they all are 2 Watts Peak.
Music is not often a square wave. Music with multiple instruments is not a single sine wave. But music is often multiple sine waves. Those sine waves often include harmonics (multiple sine waves).
Example, a clarinet often has dominant 3rd harmonic distortion.
A French horn often has dominant 2nd harmonic distortion.
Play them together, and be sure the sum of all the signals does not exceed the Peak power capability of the amplifier.
In order to properly design a 10 Watt rms amplifier, you have to calculate the necessary peak power (14.14Watts) of a 10 Watt rms sine wave.
Your formula is correct.
Consider an 8V peak to peak sine wave.
Yes, that is 2.828Vrms. That is 1 Watt rms into 8 Ohms.
But, it is 2 Watts peak into 8 Ohms.
Now, consider an 8V peak to peak square wave.
That is 4Vrms. That is 2 Watts rms into 8 Ohms.
And it is 2 watts peak into 8 Ohms.
Consider a 500 Hz sine wave that is 4 Volts peak to peak.
Consider a 700 Hz sine wave that is 4 Volts peak to peak.
Turn either tone on, and get 4 Volts peak to peak.
Turn both tones on, and get 8 Volts peak to peak.
You will get less than 1 Watt rms into 8 Ohms on a true power meter.
The peak power is 2 Watts.
The point is, the sine wave, square wave, and the two tones all have 8V peak to peak.
Each of them has a Different rms power.
But they all are 2 Watts Peak.
Music is not often a square wave. Music with multiple instruments is not a single sine wave. But music is often multiple sine waves. Those sine waves often include harmonics (multiple sine waves).
Example, a clarinet often has dominant 3rd harmonic distortion.
A French horn often has dominant 2nd harmonic distortion.
Play them together, and be sure the sum of all the signals does not exceed the Peak power capability of the amplifier.
In order to properly design a 10 Watt rms amplifier, you have to calculate the necessary peak power (14.14Watts) of a 10 Watt rms sine wave.
disco,
Suppose you want to design an 8 Watt amplifier.
8 Volts RMS into 8 Ohms is 8 Watts. Simple.
But how do you calculate an amplifier circuit that will provide a sine wave of 8 Volts RMS?
Do not do it that way.
Instead, . . .
What is the peak volts of a sine wave that is required to output 8 watts into an 8 Ohm load?
You have to be able to calculate that, or else you will either design a 6 Watt rms amplifier, a 12 Watt rms amplifier, or anything other than an 8 Watt rms amplifier.
The Peak voltage that is needed for 8 Watts has to be calculated.
I hope that helps you understand why I think about Peak Volts, and Peak Watts.
And, do not forget, we do not listen to sine wave music. Even Walter Carlos's old Moog synthesizer did not put out pure sine waves.
And most of the time, there were 2 or more notes at the same time, the Voltage addition of those notes Peaked when 2 or more notes all came into phase.
You are correct, marketing used Peak Watts in the "horsepower wars", but in so doing they negated the actual importance of peak watts.
Suppose you want to design an 8 Watt amplifier.
8 Volts RMS into 8 Ohms is 8 Watts. Simple.
But how do you calculate an amplifier circuit that will provide a sine wave of 8 Volts RMS?
Do not do it that way.
Instead, . . .
What is the peak volts of a sine wave that is required to output 8 watts into an 8 Ohm load?
You have to be able to calculate that, or else you will either design a 6 Watt rms amplifier, a 12 Watt rms amplifier, or anything other than an 8 Watt rms amplifier.
The Peak voltage that is needed for 8 Watts has to be calculated.
I hope that helps you understand why I think about Peak Volts, and Peak Watts.
And, do not forget, we do not listen to sine wave music. Even Walter Carlos's old Moog synthesizer did not put out pure sine waves.
And most of the time, there were 2 or more notes at the same time, the Voltage addition of those notes Peaked when 2 or more notes all came into phase.
You are correct, marketing used Peak Watts in the "horsepower wars", but in so doing they negated the actual importance of peak watts.
Last edited:
- Status
- This old topic is closed. If you want to reopen this topic, contact a moderator using the "Report Post" button.
- Home
- Amplifiers
- Tubes / Valves
- Emission Labs 300B Mesh in 300B Amp