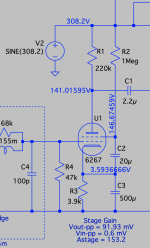
MarcelVDG has it. Another way to look at the charging time of the 500 µF cathode resistor bypass capacitor is to mentally just add the valve's nominal anode 'resistance' and the 100 kΩ load resistance together … say 100 kΩ + 16.5 kΩ (datasheet), … and the what, 250 volt B+?
GoatGuy ✓
E = IR … rearranges to
I = E/R
I = 250 ÷ 116,000
I = 2.16 mA
ΔV/Δt = I / C⋅Δt
ΔV/Δt = 0.00216 A ÷ 500×10⁻⁶ F (Δt = 1)
ΔV/Δt = 4.3 V/s … expected initial rate.
Since the expected full charge of the 500 µF bypass cap is what, 1 to 3 volts … we're looking at a full-charge time of less than 10 seconds. Well less. I = E/R
I = 250 ÷ 116,000
I = 2.16 mA
ΔV/Δt = I / C⋅Δt
ΔV/Δt = 0.00216 A ÷ 500×10⁻⁶ F (Δt = 1)
ΔV/Δt = 4.3 V/s … expected initial rate.
50% at 380 milliseconds
90% at 1,200 milliseconds
99% at 2,600 milliseconds
99.9% at 3,250 milliseconds
Just Saying,90% at 1,200 milliseconds
99% at 2,600 milliseconds
99.9% at 3,250 milliseconds
GoatGuy ✓
These "charging time" estimates, therefore time constants, therefore frequency response, are all ignoring the much smaller cathode resistor in parallel. Timing depends on the capacitor and the parallel combination of the cathode resistor and whatever the valve's cathode contributes.
All good fortune,
Chris
All good fortune,
Chris
Um… no.
The milliseconds vs. % charge calculations I did, took exactly that parallel resistance into the math. Indeed: there is a brilliantly straight-forward way to do the math using nothing more complicated than a spreadsheet; with about 5,000 lines (each representing 1 millisecond), one can do a piece-by-piece simulation which is within a few hundredths of a percent of the actual measured-in-circuit rates.
Try not to tar everyone with the same bucket of black paint.
Just Saying,
GoatGuy ✓
Fooey… I made a subtle error in the formulæ…
Sorry fellow way-before-dawn goats
GoatGuy ✓
ΔV = I⋅Δt/ C … at constant current I, so therefore
ΔV/Δt = I⋅Δt/ C⋅Δt … with the Δt/Δt cancelling to
ΔV/Δt = I/C
ΔV/Δt = 0.00216 A ÷ 500×10⁻⁶ F
Note that the bottom line is the same, but the cancellation of Δt wasn't done right to start with.ΔV/Δt = I⋅Δt/ C⋅Δt … with the Δt/Δt cancelling to
ΔV/Δt = I/C
ΔV/Δt = 0.00216 A ÷ 500×10⁻⁶ F
Sorry fellow way-before-dawn goats
GoatGuy ✓
Last edited:
As a general rule, I use about 1000uF to bypass a cathode resistor, but I rarely bypass in the first place.
I haven't tried these ones yet, but the computer geek in me thinks they would be damned good and probably outlast the amp (20000 hours, 105c)
APSG160ELL102MH20S United Chemi-Con | Capacitors | DigiKey
I haven't tried these ones yet, but the computer geek in me thinks they would be damned good and probably outlast the amp (20000 hours, 105c)
APSG160ELL102MH20S United Chemi-Con | Capacitors | DigiKey
I neglected the cathode resistor, assuming it to be >> 1/(gm + gm_screen), but in fact it is of the same order of magnitude, so please replace 1/(gm + gm_screen) with 1/(gm + gm_screen + 1/RK). In any case, it is still a matter of a few seconds.
Last edited:
These discussions are great, thank you!
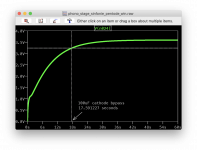
I changed the bypass in my model to see how the charging looked. I tried out a 1000uF too.
With a 100uF cap, it took about 17.6 seconds to get to 90%.
With a 500uF cap, it took about 19.2 seconds to get to 90%.
With a 1000uF cap, it took about 21.5 seconds to get to 90%.
Interesting that there is so little difference in time despite the huge difference in cap sizes.
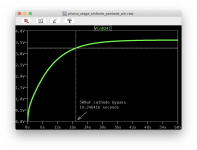
I changed the bypass in my model to see how the charging looked. I tried out a 1000uF too.
With a 100uF cap, it took about 17.6 seconds to get to 90%.
With a 500uF cap, it took about 19.2 seconds to get to 90%.
With a 1000uF cap, it took about 21.5 seconds to get to 90%.
Interesting that there is so little difference in time despite the huge difference in cap sizes.
