Hello,
I'm new to DIY audio. I have had a misunderstanding that has been puzzling me about dynamic speaker frequency response. I have seen explanations about these kinds of speakers comparing them to a mass-spring system under forced oscillation. I have studied these systems in physics courses so I'm familiar with the response curves showing amplitude at various damping factors.
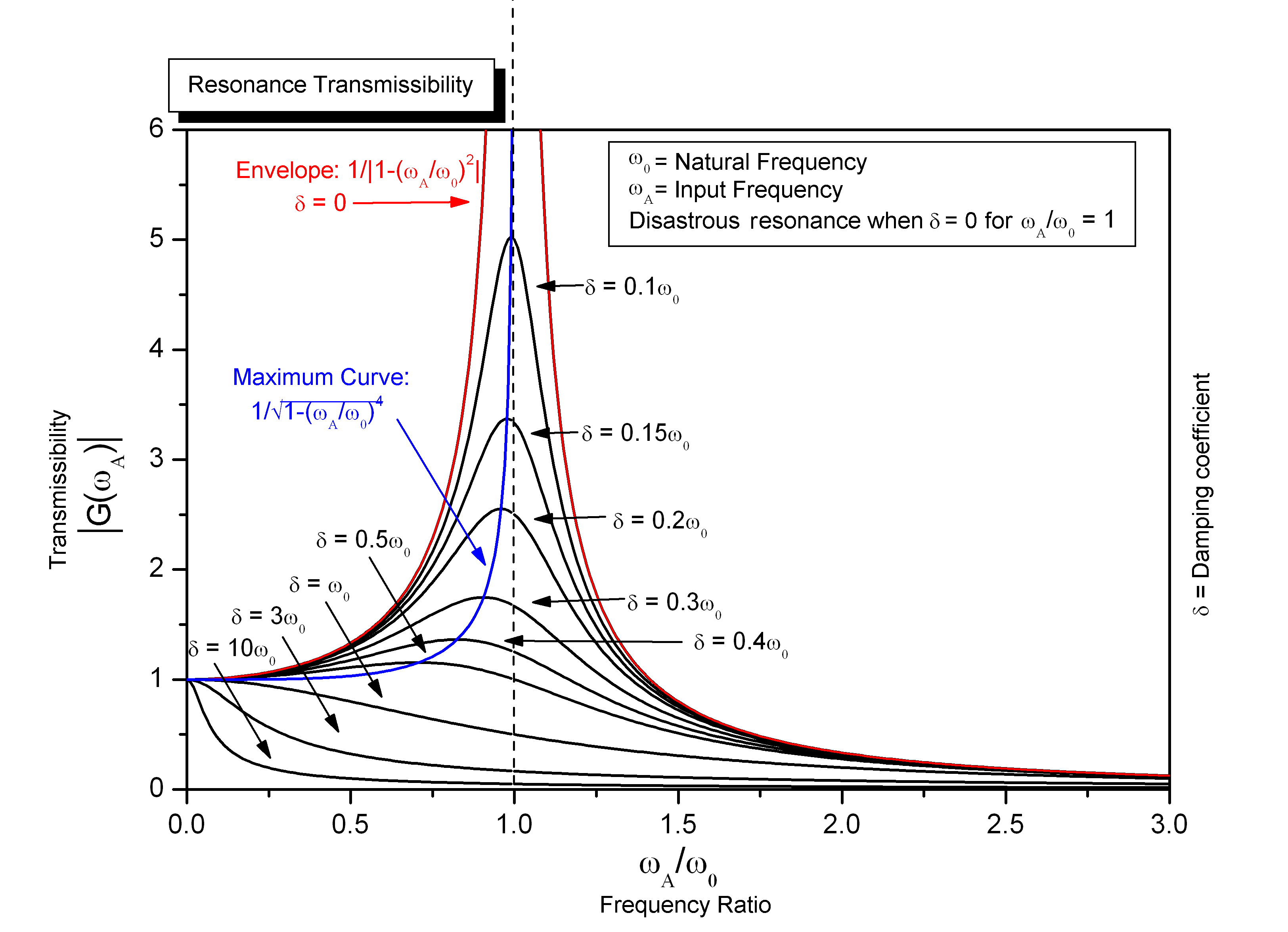
These curves show at below resonance that the amplitude follows the input amplitude, peaks at the resonance frequency, then above resonance the amplitude falls away with increasing frequency. Generally the shape is a low-pass behavior with the resonance frequency defining the transition point.
When I look at frequency responses for woofers and subwoofers, the exact opposite behavior shows up:
These show a high-pass behavior, not a low-pass behavior. Am I missing something or thinking about this the wrong way?
I'm new to DIY audio. I have had a misunderstanding that has been puzzling me about dynamic speaker frequency response. I have seen explanations about these kinds of speakers comparing them to a mass-spring system under forced oscillation. I have studied these systems in physics courses so I'm familiar with the response curves showing amplitude at various damping factors.
These curves show at below resonance that the amplitude follows the input amplitude, peaks at the resonance frequency, then above resonance the amplitude falls away with increasing frequency. Generally the shape is a low-pass behavior with the resonance frequency defining the transition point.
When I look at frequency responses for woofers and subwoofers, the exact opposite behavior shows up:
These show a high-pass behavior, not a low-pass behavior. Am I missing something or thinking about this the wrong way?
Last edited:
There are resonances at both the bottom and the top of the range,
so there is bandpass behavior. See chapter 7 (and fig. 7.6) here:
https://cdn.preterhuman.net/texts/s...and_Thermodynamics/Acoustics - L. Beranek.pdf
Last edited:
Sorry but you are looking at it the wrong way 🙁Hello,
I'm new to DIY audio. I have had a misunderstanding that has been puzzling me about dynamic speaker frequency response. I have seen explanations about these kinds of speakers comparing them to a mass-spring system under forced oscillation. I have studied these systems in physics courses so I'm familiar with the response curves showing amplitude at various damping factors.
These curves show at below resonance that the amplitude follows the input amplitude, peaks at the resonance frequency, then above resonance the amplitude falls away with increasing frequency. Generally the shape is a low-pass behavior with the resonance frequency defining the transition point.
When I look at frequency responses for woofers and subwoofers, the exact opposite behavior shows up:
These show a high-pass behavior, not a low-pass behavior. Am I missing something or thinking about this the wrong way?
You are comparing different phenomenae.
Your curve showing the mass loaded spring shows spring displacement vs. excitation/driving force, and of course is right.
You should compare it to a speaker curve showing cone displacement amplitude vs excitation, and in that case you may very well find them quite similar or at least comparable.
BUT you are not showing that, by any means.
Your speaker curve clearly depicts Sound Pressure Level vs. excitation, a completely different phenomenon, not even units match. 😱
Hope this clears your doubt. 🙂
The thing that has been missed isn't what's posted above. It's this:
In order to maintain constant SPL, you need 4x the cone displacement per halving of frequency.
Put another way, a speaker that has constant excursion vs frequency will have a response that falls at 12dB/octave as frequency decreases.
When you account for that, the curves both tell the same story.
Chris
In order to maintain constant SPL, you need 4x the cone displacement per halving of frequency.
Put another way, a speaker that has constant excursion vs frequency will have a response that falls at 12dB/octave as frequency decreases.
When you account for that, the curves both tell the same story.
Chris
Is SPL not a direct function of cone displacement? Power of a sinusoid tends to follow a amplitude^2 relationship. If that's the case then the DispX vs Freq graphs would still give us an adequate representation of SPL vs Freq.
So you're saying there is a inverse relationship of freq^2 vs SPL and a direct relationship between amplitude and SPL?
In other words SPL ~ Ampl/freq^2
Your graph does NOT show DispX vs Freq but SPL vs Freq.
Yet again: the second graph is labelled "amplitude" which implies a physical displacement measurable in distance units (say mm for example) but actually shows Sound Pressure which uses absolutely different units.
Poor use of the word "amplitude" in this case.
That both can be correlated using a third equation or graph (which you do not show) is of secondary importance compared to this conceptual error.
I am talking about what was actually written, not what might/should have been.
As chris661 already wrote in other words, at low frequencies (within the piston range), the sound pressure level depends on the acceleration rather than the displacement of the cone.
The T/S model only addresses the fundamental resonance, which determines the high pass behavior. The low pass behavior can be treated separately and has its own resonances, which are tougher to describe mathematically (often requiring numerical solution on a computer using perhaps a finite-element method). It is the poles of the filter function (high pass, low pass or band pass) which determine the Q, which determine the magnitude of the peaking or damping of the resonance at the corner frequency. The same poles have the same relative peaking behavior, high or low pass. Where the zeros of the filter function are determine if it is low pass or high pass. For high pass, the zeros are at DC, or zero frequency. For low pass, the zeros are at infinite frequency. Since the displacement or SPL of a speaker cannot be other than zero at zero frequency the fundamental (or lowest frequency) resonance must be high pass with zeros at zero. Yes there is displacement at DC (if you hook a battery to it), but it’s behavior is non linear, so linear network theory doesn’t apply.
All this makes more sense after your first college courses in EE.
- Status
- Not open for further replies.