We know a larger horn mouth has a lower cutoff frequency.
We know multicell horns work as a single horn with regards to cutoff.
What would happen if I stick two or more identical horns closely together on a baffle if they each are driven by their own compression driver. Do they "sum" to a lower cutoff?
And if they do how close together must they be?
We know multicell horns work as a single horn with regards to cutoff.
What would happen if I stick two or more identical horns closely together on a baffle if they each are driven by their own compression driver. Do they "sum" to a lower cutoff?
And if they do how close together must they be?
zero length:
https://www.linkwitzlab.com/diffraction.htm
throat size, mouth size, length, flare rate are inevitably linked together for true exponential horns. The point is where you terminate the horn and this makes the difference.
Indeed. I just think there are more fundamental misunderstandings related to this which are quite common and should be cleared up first. Waveguides for example have no cutoff, yet are often described in mouth wavelengths. Every horn is different.
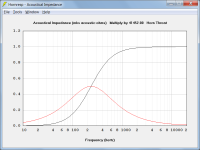
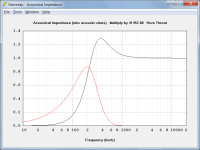
An OS waveguide is a bit different to a conical horn in that it can be considered to have a cutoff frequency, given by the empirical formula:
F12 = 0.2 * c * Sin(Theta / 180 * Pi) / Sqrt(S1 * Pi)
Where:
F12 = cutoff frequency
c = speed of sound
Theta = OS waveguide coverage half-angle (in degrees)
S1 = throat area
For example, given an OS waveguide with:
S1 = 100 cm^2
S2 = 2800 cm^2
L12 = 100 cm
AT = throat entry half-angle = 0 degrees
Theta is:
16.34 degrees
If c = 34400 cm/sec then:
F12 = 0.2 * 34400 * Sin(16.34 / 180 * Pi) / Sqrt(100 * Pi)
F12 = 109.20 Hz
The two attachments show the normalised throat acoustical impedance for an infinite conical horn and equivalent OS waveguide.
Attachments
Yes, this is correct. I think the problem is that I oversimplified it while trying to make a point in the bigger picture.
It's notable in my opinion that cutoff in a waveguide is not of so much consequence. You can push down through it without being aware of it. Cutoff can also be confused with the nominal lower frequency of directivity control, which might be more applicable to the average waveguide.
It's notable in my opinion that cutoff in a waveguide is not of so much consequence. You can push down through it without being aware of it. Cutoff can also be confused with the nominal lower frequency of directivity control, which might be more applicable to the average waveguide.
