Then the answer is 0 Hz. It is by (your) definition 0 dB at 0 Hz, and it starts to drop immediately above 0 Hz, although it goes quite slow at first.
Edit: Sorry, I had overlooked your edit of post #16.
Edit: Sorry, I had overlooked your edit of post #16.
Interesting. If you plot such a curve in software, it displays as 0 dB up to somewhere in the 1kHz to 3 kHz range. I'd be interested to see a table of values for various first-order rolloff curves for various 10 kHz attenuation values. It sounds like these all leave 0 dB right at 0 Hz, but I'd be interested to know where they "statistically significantly" leave 0 dB, if that makes sense, e.g. where they're -0.25 dB. The reason for my curiousity is that CEDAR Cambridge IIR IQ module has some odd input controls, and the curves seem a little incorrect at lower frequencies than the 3dB points...it's good to have several reference points to ensure accuracy. If you plot another point in the EQ software, one can fudge the curve above the transition frequency to the correct value. Sorry if the prior posts are a little scatter-brained. This is a hobby and I tend to learn the things I need to know as I go rather than, say, go to audio engineering school...The 78 world is rather underserved. Armchair engineers are regularly putting out far superior projects to the major labels and saving things that would otherwise get mulched by yokel Victrola collectors with their two pound sound boxes.
| 10 kHz Attenuation | Transition Frequency (& Time Constant) (-3dB point) | |||||
| –5 dB |
| |||||
| –7 dB |
| |||||
| –8.5 dB |
| |||||
| –10 dB |
| |||||
| –10.5 dB |
| |||||
| –12 dB (AES) | 2595 Hz (61.33 μS) | |||||
| –13.73 dB (RIAA) | 2122 Hz (75 μS) | |||||
| –14 dB |
| |||||
| –15 dB |
| |||||
–16 dB (NAB and
| 1591.55 Hz (100.0 μS) | |||||
| –20 dB | 1005 Hz (158.36 μS) | |||||
Last edited:
Regarding inverse RIAA, I read Scott Wurcer's article. It is a pity he is no longer active on this forum.
Scott's article is quite thorough. Unfortunately some of the tables at the end seem to be messed up; I saw tables for 48 kHz and 96 kHz sample rate that looked exactly the same while they should be different. Fortunately they can also be downloaded from the Linear Audio website without these errors:
https://linearaudio.net/downloads
Scroll down to heading: "Test waveforms for Scott Wurcer's digital RIAA article in Volume 10"
Tables:
https://linearaudio.net/sites/linearaudio.net/files/v10 sw app1 table a-1.xlsx
for optimized IIR filter coefficients for RIAA equalization with one biquad at 48 kHz, 96 kHz and 192 kHz sample rates. Using only one biquad results in a +/- 0.13 dB error at 48 kHz, much less at higher sample rates.
For more accurate correction using two separate biquads at 48 kHz and 96 kHz sample rates:
https://linearaudio.net/sites/linearaudio.net/files/v10 sw Appendix 1b web.docx
This table contains IIR filter coefficients for RIAA correction as well as for various other types of correction for old records.
To get from RIAA correction to inverse RIAA, you have to swap the a and the b coefficients. That is, ai becomes bi and the other way around.
By adding one or two more biquads with the archival correction coefficients (not swapped), you get a chain of three or four biquads that converts RIAA correction into the archival correction.
The coefficients are not normalized to 0 dB gain at 1 kHz, but that's a matter of adding one multiplication with a gain constant.
According to the article, the Audacity Nyquist syntax for a biquad is biquad-m signal b0 b1 b2 a0 a1 a2. The SoX syntax is biquad a0 a1 a2 b0 b1 b2.
Scott's article is quite thorough. Unfortunately some of the tables at the end seem to be messed up; I saw tables for 48 kHz and 96 kHz sample rate that looked exactly the same while they should be different. Fortunately they can also be downloaded from the Linear Audio website without these errors:
https://linearaudio.net/downloads
Scroll down to heading: "Test waveforms for Scott Wurcer's digital RIAA article in Volume 10"
Tables:
https://linearaudio.net/sites/linearaudio.net/files/v10 sw app1 table a-1.xlsx
for optimized IIR filter coefficients for RIAA equalization with one biquad at 48 kHz, 96 kHz and 192 kHz sample rates. Using only one biquad results in a +/- 0.13 dB error at 48 kHz, much less at higher sample rates.
For more accurate correction using two separate biquads at 48 kHz and 96 kHz sample rates:
https://linearaudio.net/sites/linearaudio.net/files/v10 sw Appendix 1b web.docx
This table contains IIR filter coefficients for RIAA correction as well as for various other types of correction for old records.
To get from RIAA correction to inverse RIAA, you have to swap the a and the b coefficients. That is, ai becomes bi and the other way around.
By adding one or two more biquads with the archival correction coefficients (not swapped), you get a chain of three or four biquads that converts RIAA correction into the archival correction.
The coefficients are not normalized to 0 dB gain at 1 kHz, but that's a matter of adding one multiplication with a gain constant.
According to the article, the Audacity Nyquist syntax for a biquad is biquad-m signal b0 b1 b2 a0 a1 a2. The SoX syntax is biquad a0 a1 a2 b0 b1 b2.
Cool, I think this is starting to converge with the Wayne Stegall application I linked in the original post. I've been busy and haven't had time to try to untangle this, but I'm guessing if I use his program and plug in -18.62517791 dB of gain, his inverse RIAA curve would be exactly what I'm looking for. Need to compare the values and try to figure out how to get the "biquad-m signal b0 b1 b2 a0 a1 a2" syntax correct. Still a new concept. I want to be sure the multiplication of the gain constant is correctly computed.
Those other resources look really great.
Those other resources look really great.
Just turn the equation inside out:
G = -10 dB*log10(1 + (f/fc)2)
-G/(10 dB) = log10(1 + (f/fc)2)
10-G/(10 dB) -1 = (f/fc)2)
f = fc sqrt(10-G/(10 dB) -1)
For fc ~= 6800.553621 Hz and G = -0.25 dB: f ~= 1655.396752 Hz.
Great!
Could I trouble you to compute the ideal 96 khz reverse RIAA Audacity biquad normalized for 1 kHz at 0dB? I probably could if I spent a long time reading all the background info, but this is pretty critical and I want the assurance that someone who knows what they're doing vetted it.
Could I trouble you to compute the ideal 96 khz reverse RIAA Audacity biquad normalized for 1 kHz at 0dB? I probably could if I spent a long time reading all the background info, but this is pretty critical and I want the assurance that someone who knows what they're doing vetted it.
This might help:
(Definitions of "Turnover" and "Tip" frequencies can be inferred from RIAA spec.)
Bass Tip/Bass Turnover/Treble Turnover combinations
---------------------------------------------------
/ 150/ 3.4k Decca
/ 150/ 5.8k early Decca
/ 200/ flat Westrex
/ 200/ 5.8k Columbia 1925
40/ 200/ 6.36k American 1025, Victor 1925 (some)
50/ 250/ flat Blumlein, HMV
/ 250/ flat Columbia (Eng.), EMI 1931
40/ 250/ 6.36k London FFRR 1949, FFRR 78
/ 300/ 1.6k Columbia 1938
/ 300/ 2k FFRR 1951
50/ 353/ 3.18k BSI
/ 375/ 2.5k Decca 1934
/ 375/ 5.8k Decca FFRR 1949, EMI
/ 375/ 6.36k Decca FFRR 1949, EMI, Victor 1925 (some)
70/ 400/ flat early 78 (mid-'30s), US mid 30
/ 400/ 2.5k old AES, Decca 1934, Mercury
100/ 450/ 3k FFRR 1953
/ 500/ flat early 78, Brunswick, Parlophone
100/ 500/ 1590 Columbia LP
/ 500/ 1590 early LP
/ 500/ 1.6k early LP, NAB, NARTB
70/ 500/ 2.5k EMI
/ 500/ 2.5k Capitol 1942, MGM, Victor 1947-1952
100/ 500/ 3k FFRR
50/ 500/ 3.18k CCIR
/ 500/ 3.18k London FFRR
/ 500/ 3.4k Concert Hall until 1952, Oiseau-Lyre until 1954
/ 500/ 5.8k Victor 1938-1947
50.05/500.5/2.122k RIAA
/ 629/ flat "629"
/ 800/ 2.5k early RCA
Something else to be aware of. From the December 2002 issue of Mix magazine:
"It's a little-known fact that record labels adopted a number of
'standard' speeds for 78 rpm discs that ranged from 71.29 to 80 rpm. In
fact, the standard for 'modern' 78s (spanning the period from the mid-1920s
through the 1950s) was actually 78.26 rather than 78.00 rpm. Play an early
Victor disc (intended for 71.29 rpm playback) on a typical modern turntable
and the pitch change is nearly +10% (approximately 160 cents sharp) -- over
a step and a half! I cringe whenever I hear a 78 reissue where the engineers
or producers didn't bother to play back the disc at the right speed.
"Here are some 'standard' speeds that are used by various record
labels: 71.29 rpm -- Berliner, Zonaphone and early Victor; 76.59 rpm --
Victor acoustic (through the mid-1920s); 80.00 rpm -- acoustic Columbia,
Edison, Pathe, Emerson, Brunswick and Okeh; and 78.26 rpm -- the 'electric'
recording standard, eventually adopted by all labels from the mid-1920s
onward. Early examples of electrically recorded discs included Victor's
'Orthophonic' and Columbia's 'Viva-Tonal' releases."
"It's a little-known fact that record labels adopted a number of
'standard' speeds for 78 rpm discs that ranged from 71.29 to 80 rpm. In
fact, the standard for 'modern' 78s (spanning the period from the mid-1920s
through the 1950s) was actually 78.26 rather than 78.00 rpm. Play an early
Victor disc (intended for 71.29 rpm playback) on a typical modern turntable
and the pitch change is nearly +10% (approximately 160 cents sharp) -- over
a step and a half! I cringe whenever I hear a 78 reissue where the engineers
or producers didn't bother to play back the disc at the right speed.
"Here are some 'standard' speeds that are used by various record
labels: 71.29 rpm -- Berliner, Zonaphone and early Victor; 76.59 rpm --
Victor acoustic (through the mid-1920s); 80.00 rpm -- acoustic Columbia,
Edison, Pathe, Emerson, Brunswick and Okeh; and 78.26 rpm -- the 'electric'
recording standard, eventually adopted by all labels from the mid-1920s
onward. Early examples of electrically recorded discs included Victor's
'Orthophonic' and Columbia's 'Viva-Tonal' releases."
Thanks, very aware. I pitch everything before transferring and use each label's curve. There's no standard speed. One side from a session can be half a percent different from the other side. One day, the lathe ran at 76, the next at 81.5. Did the band really play that jazz tune in the key of B? No, obviously Bb or C. Your ears will tell you which is correct. You can also sometimes use the electrical hum to hone in, but even that wasn't very standardized in the 20s.
I think I have a good handle on reverse engineering and implementing the period curves. The one thing I'm still a little shaky on is the optimal reverse RIAA Nyquist command for 96 kHz with 1 Khz at 0 dB. I have one tentative answer from elsewhere, but I'd feel more comfortable if I could see someone who is more comfortable with Nyquist and the associated math corroborate and maybe show a little work. Hopefully not too much of an ask. Most of the info needed to figure that out is posted above. I checked the tentative solution last night, and it sounded basically identical to the same record played with truly-flat emphasis, but the very low and very high frequencies looked somewhat different, so I'm not sure the gain is exactly correct on that solution. More testing needed. It's hard to tell with the actually-flat material because the recordings are full of transients from the shellac, even if the record is clean.
I think I have a good handle on reverse engineering and implementing the period curves. The one thing I'm still a little shaky on is the optimal reverse RIAA Nyquist command for 96 kHz with 1 Khz at 0 dB. I have one tentative answer from elsewhere, but I'd feel more comfortable if I could see someone who is more comfortable with Nyquist and the associated math corroborate and maybe show a little work. Hopefully not too much of an ask. Most of the info needed to figure that out is posted above. I checked the tentative solution last night, and it sounded basically identical to the same record played with truly-flat emphasis, but the very low and very high frequencies looked somewhat different, so I'm not sure the gain is exactly correct on that solution. More testing needed. It's hard to tell with the actually-flat material because the recordings are full of transients from the shellac, even if the record is clean.
Last edited:
I'm not sure that I understand the problem. If you have an implementation of the reverse RIAA with 0 dB at 20 kHz, for example, and you want 0 dB to be at 1 kHz, then all you need to do is change the gain. To change the gain of a biquad, just multiply all of the numerator coefficients by the gain adjustment value. If you want to distribute that gain change across multiple biquads, then just make certain that the product of the individual gain adjustments equals the total gain adjustment. (For example, if your total gain adjustment is 4, and you have two biquads, then the numerator coefficients of each biquad could be multiplied by 2.)
Just be aware that implementing a gain of ~20 dB in digital can be very dangerous. You can cause internal digital clipping without even realizing it.
I understand the basics. The synthesis of the concepts is just a little confusing for someone who's never really studied Nyquist.
So:
The formula template is
biquad-m signal b0 b1 b2 a0 a1 a2.
Sampling Frequency 96 kHz
-13.73dB (RIAA)
poles = [2118.61024386, 46671.0547377]
zeros = [33577.71203556, 59118.30187446]
a coefficients = [ 1. -0.66168391 -0.18158841]
b coefficients = [ 1. 0.3655731 0.01499662]
Gain at 1kHz = 18.0272664045 dB
50.05 Hz and 500.5 Hz (RIAA)
poles = [50.0499639758, 69998.9836645]
zeros = [500.455331485, 70001.7913378]
a coefficients = [ 1. -0.60450091 -0.39094593]
b coefficients = [ 1. -0.57552742 -0.37960478]
Gain at 1kHz = 0.832424759841 dB
This is where I'm not really sure what to do. Sum the gains...so 18.859691164341. Then multiply each of the coefficients by -18.85... Then sum them and put them into the formula template, but swapped because it's inverted? Easy to mess up for a first-timer.
So:
The formula template is
biquad-m signal b0 b1 b2 a0 a1 a2.
Sampling Frequency 96 kHz
-13.73dB (RIAA)
poles = [2118.61024386, 46671.0547377]
zeros = [33577.71203556, 59118.30187446]
a coefficients = [ 1. -0.66168391 -0.18158841]
b coefficients = [ 1. 0.3655731 0.01499662]
Gain at 1kHz = 18.0272664045 dB
50.05 Hz and 500.5 Hz (RIAA)
poles = [50.0499639758, 69998.9836645]
zeros = [500.455331485, 70001.7913378]
a coefficients = [ 1. -0.60450091 -0.39094593]
b coefficients = [ 1. -0.57552742 -0.37960478]
Gain at 1kHz = 0.832424759841 dB
This is where I'm not really sure what to do. Sum the gains...so 18.859691164341. Then multiply each of the coefficients by -18.85... Then sum them and put them into the formula template, but swapped because it's inverted? Easy to mess up for a first-timer.
Using the coefficients as-provided, I get the magnitude plot labeled "Coefficients as Provided". If I swap the numerators and denominators, i.e., the "a" coefficients become the numerators and the "b" coefficients become the denominators, I get the magnitude plot labeled "Biquads Inverted". You probably understand enough to take if from there.
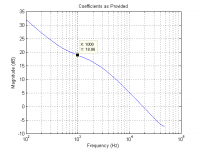
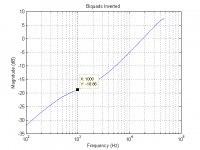
Could someone explain this to me like I'm a child and just post the exact command in Audacity syntax? Like I said, I have NO Nyquist experience and I am having trouble figuring out how the numerator and denominator come together from the two pole/zero sets and how to get the figure into the e+00 syntax.
One formula I have for this is as follows. This might be correct, but I don't know how it was computed.
(biquad-m track 5.196122e+00 -6.324336e+00 1.253910e+00 1.000000e+00 -7.206742e-01 0.000000e+00)
If I plug the following into my RIAAIR app, I get this:
Filter calculated for:
Sampling frequency: 96000
Gain: -18.8597
Extra zero: 0
Inverse: 1
Coefficients for H(z)
num[0] = -1.433161e+003, [1] = 2.675789e+003, [2] = -1.243236e+003
-------------------------------------------------------------------
den[0] = 1.000000e+000, [1] = -9.677739e-001
Audacity Nyquist biquad equations (LISP format)
(biquad s b0 b1 b2 a0 a1 a2)
(biquad s -1.433161e+003 2.675789e+003 -1.243236e+003 1.0 9.677739e-001 -0.000000e+000)
(biquad-m s b0 b1 b2 a0 a1 a2)
(biquad-m s -1.433161e+003 2.675789e+003 -1.243236e+003 1.000000e+000 -9.677739e-001 0.000000e+000)
This seems to be wrong.
What, please, is the Audacity-syntax formula, for the Scott Wurcer values?
One formula I have for this is as follows. This might be correct, but I don't know how it was computed.
(biquad-m track 5.196122e+00 -6.324336e+00 1.253910e+00 1.000000e+00 -7.206742e-01 0.000000e+00)
If I plug the following into my RIAAIR app, I get this:
Filter calculated for:
Sampling frequency: 96000
Gain: -18.8597
Extra zero: 0
Inverse: 1
Coefficients for H(z)
num[0] = -1.433161e+003, [1] = 2.675789e+003, [2] = -1.243236e+003
-------------------------------------------------------------------
den[0] = 1.000000e+000, [1] = -9.677739e-001
Audacity Nyquist biquad equations (LISP format)
(biquad s b0 b1 b2 a0 a1 a2)
(biquad s -1.433161e+003 2.675789e+003 -1.243236e+003 1.0 9.677739e-001 -0.000000e+000)
(biquad-m s b0 b1 b2 a0 a1 a2)
(biquad-m s -1.433161e+003 2.675789e+003 -1.243236e+003 1.000000e+000 -9.677739e-001 0.000000e+000)
This seems to be wrong.
What, please, is the Audacity-syntax formula, for the Scott Wurcer values?
I think I'm missing some key concepts here. For example, this isn't making sense:
The gains given for the two parts can be used to compute a net gain in order to adjust for the desired gain at 1 kHz. I would recommend splitting the difference i.e. if the gains for the two filters are 5dB and 7dB and you want a gain of 20dB at 1 kHz you would add 4dB to each (9dB and 11dB), so the sets of b coefficients would be multiplied by 2.8184 and 3.5481 respectively.
What is the math to get the 2.81 and 3.54 values? 5*2.81 is roughly 14, not 9.
***
Based on the above, I think my coefficients are:
B COEFFICIENTS (listed as A coefficients above, but inverted here)
[ 1. -0.66168391 -0.18158841]
[ 1. -0.60450091 -0.39094593]
A COEFFICIENTS (listed as B coefficients above, but inverted here)
[ 1. 0.3655731 0.01499662]
[ 1. -0.57552742 -0.37960478]
How does this correspond to b0, b1, b2, a0, a1, a2? Is b0 and a0 1? I think the denominator is only supposed to have two values rather than three, so I'm pretty lost on how I'm supposed to convert the above coefficients into the Audacity LISP format. Do I sum the 0, 1, and 2 values for each of the halves of the biquad? It sounds like there might need to be two separate biquads. A lot of ways to attack this, it seems. I guess I need to spit the 18.8597 dB between the two halves of the biquad.
Do you just throw out A2 and call it 0.0000e+00?
This is rambling and inane...help!
The gains given for the two parts can be used to compute a net gain in order to adjust for the desired gain at 1 kHz. I would recommend splitting the difference i.e. if the gains for the two filters are 5dB and 7dB and you want a gain of 20dB at 1 kHz you would add 4dB to each (9dB and 11dB), so the sets of b coefficients would be multiplied by 2.8184 and 3.5481 respectively.
What is the math to get the 2.81 and 3.54 values? 5*2.81 is roughly 14, not 9.
***
Based on the above, I think my coefficients are:
B COEFFICIENTS (listed as A coefficients above, but inverted here)
[ 1. -0.66168391 -0.18158841]
[ 1. -0.60450091 -0.39094593]
A COEFFICIENTS (listed as B coefficients above, but inverted here)
[ 1. 0.3655731 0.01499662]
[ 1. -0.57552742 -0.37960478]
How does this correspond to b0, b1, b2, a0, a1, a2? Is b0 and a0 1? I think the denominator is only supposed to have two values rather than three, so I'm pretty lost on how I'm supposed to convert the above coefficients into the Audacity LISP format. Do I sum the 0, 1, and 2 values for each of the halves of the biquad? It sounds like there might need to be two separate biquads. A lot of ways to attack this, it seems. I guess I need to spit the 18.8597 dB between the two halves of the biquad.
Do you just throw out A2 and call it 0.0000e+00?
This is rambling and inane...help!
Last edited:
You want a gain of 20 dB total. One of the filters already has a gain of 5 dB and the other already has a gain of 7 dB, for a total of 12 dB. You need 8 dB more to achieve 20 dB total. You can add 4 dB to each filter so that the first now has (5+4=9) dB and the second has (7+4=11) dB.
9 dB is equivalent to multiplication by 10^(9/20) = 2.818, and 11 dB is equivalent to multiplication by 10^(11/20) = 3.548.
There are two biquads shown here. The first has numerator (B coefficients) [ 1. -0.66168391 -0.18158841] and denominator (A coefficients) [ 1. 0.3655731 0.01499662]. So in the [b0, b1, b2, a0, a1, a2] format, it will be [1. -0.66168391 -0.18158841 1. 0.3655731 0.01499662]. The second has numerator [ 1. -0.60450091 -0.39094593] and denominator [ 1. -0.57552742 -0.37960478], so in [b0, b1, b2, a0, a1, a2] format, it will be [ 1. -0.60450091 -0.39094593 1. -0.57552742 -0.37960478].
I cannot help you with Audacity LISP, having no experience with it. Why do you think that the denominator should only have two coefficients? A standard biquad has three numerator and three denominator coefficients. Be aware, though, that a common practice is to normalize a biquad so that the a0 coefficient is 1.0, in which case a0 need not be specified as its value is assumed.
Perfect, that helped me crack the code, I hope...going to try it now
Because I need to reduce the inverse curve by 18.85dB, I subtracted 9.428 dB from each of the two biquads, i.e. 10^(9.4298/20) = -2.961
So
B0 B1 B2
_________
A0 A1 A2
[ 1. -0.66168391 -0.18158841] ALL MULTIPLIED BY -2.961
______________________________________
[ 1. 0.3655731 0.01499662]
[ 1. -0.60450091 -0.39094593] ALL MULTIPLIED BY -2.961
________________________________
[ 1. -0.57552742 -0.37960478]
(biquad-m * track * -2.96136732e+00 1.95948911e+00 5.37749983e-01 1.000000e+00 03.655731e-01 1.499662e-02)
(biquad-m * track * -2.96136732e+00 1.70434809e+00 1.12414919e+00 1.000000e+00 -5.7552742e-01 -3.7960478e-01)
Because I need to reduce the inverse curve by 18.85dB, I subtracted 9.428 dB from each of the two biquads, i.e. 10^(9.4298/20) = -2.961
So
B0 B1 B2
_________
A0 A1 A2
[ 1. -0.66168391 -0.18158841] ALL MULTIPLIED BY -2.961
______________________________________
[ 1. 0.3655731 0.01499662]
[ 1. -0.60450091 -0.39094593] ALL MULTIPLIED BY -2.961
________________________________
[ 1. -0.57552742 -0.37960478]
(biquad-m * track * -2.96136732e+00 1.95948911e+00 5.37749983e-01 1.000000e+00 03.655731e-01 1.499662e-02)
(biquad-m * track * -2.96136732e+00 1.70434809e+00 1.12414919e+00 1.000000e+00 -5.7552742e-01 -3.7960478e-01)
It worked, but the gain looks way too high compared to the flat comparison track I made. Guess something got lost in translation. I guess now I have the tools needed to figure it out...
I think I must have misinterpreted the gain figures for each of the halves of the curve...
For the 500 Hz turnover: Gain at 1kHz = 0.832424759841 dB. Probably need to just add that amount back in rather than 9 dB. Same with the other half.
I think I must have misinterpreted the gain figures for each of the halves of the curve...
For the 500 Hz turnover: Gain at 1kHz = 0.832424759841 dB. Probably need to just add that amount back in rather than 9 dB. Same with the other half.