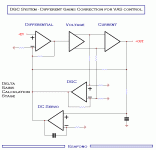
the concept of correcting the different gains
between two branches of VAS
through the use of an OP-AMP is an important novelty
to bring the solid state to the sound of valves
the difference in gain between devices PNP and NPN
is constantly monitored and corrected by a differential amplifier
see the original schematic here
http://www.esafono.it/a700.pdf

between two branches of VAS
through the use of an OP-AMP is an important novelty
to bring the solid state to the sound of valves
the difference in gain between devices PNP and NPN
is constantly monitored and corrected by a differential amplifier
see the original schematic here
http://www.esafono.it/a700.pdf

Attachments
Hi Xeye,
I fail to see how this schema would work.
You indicated that this is for correcting the different amplification of the two VAS stages. You take an error signal, and apply it to both VAS amplifier again. So it will influence both channels, not just one.
This is just a quick comment. To verify if this is true, you would have to write up the amplification equations for both channels (you can just use ideal amplifier blocks, with K1 and K2 amplifications), apply the feedback, and see if the error diminishes.
The other method would be the brute force method, by plugging in the the circuits (both the original, and yours) into SPICE, and see if you get lesser error.
Good luck, Peter
I fail to see how this schema would work.
You indicated that this is for correcting the different amplification of the two VAS stages. You take an error signal, and apply it to both VAS amplifier again. So it will influence both channels, not just one.
This is just a quick comment. To verify if this is true, you would have to write up the amplification equations for both channels (you can just use ideal amplifier blocks, with K1 and K2 amplifications), apply the feedback, and see if the error diminishes.
The other method would be the brute force method, by plugging in the the circuits (both the original, and yours) into SPICE, and see if you get lesser error.
Good luck, Peter
- Status
- Not open for further replies.