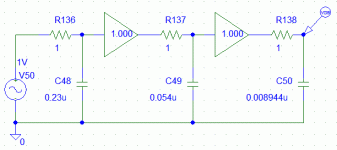
Hi to u all. I am stuck with a problem for which I need your help. I want to solve a complex equation but I do not know how to proceed. The equation is given below.
1=(1+(0.7Mhz/0.7Mhz)2)(1+(0.7Mhz/3Mhz)2)(1+(0.7Mhz/18Mhz)2)
The 0.7Mhz is the first break frequency of an amplier response curve. 3Mhz and 18Mhz are the other break frequencies. I am eager for any sound explanations and thank uin advance
1=(1+(0.7Mhz/0.7Mhz)2)(1+(0.7Mhz/3Mhz)2)(1+(0.7Mhz/18Mhz)2)
The 0.7Mhz is the first break frequency of an amplier response curve. 3Mhz and 18Mhz are the other break frequencies. I am eager for any sound explanations and thank uin advance
This is the statement I can read:
1 = { [ 1 + (0.7/0.7)exp2 ] * [ 1 + (0.7/3.0)exp2 ] * [ 1 + (0.7/18)exp2 ] }
1 = { [ 2 ] * [ 1.054... ] * [ 1.0015... ] }
1 = { 2.111... }
Which is not true.
(solved)
1 = { [ 1 + (0.7/0.7)exp2 ] * [ 1 + (0.7/3.0)exp2 ] * [ 1 + (0.7/18)exp2 ] }
1 = { [ 2 ] * [ 1.054... ] * [ 1.0015... ] }
1 = { 2.111... }
Which is not true.
(solved)
Can you show the original equation? Complex equations have an i (sqrt -1) usually a j in EE land in them.
Complex math two
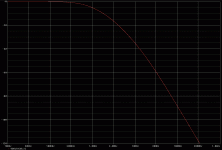
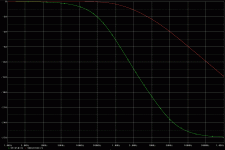
Hi to u all.sorry for late reply.that same evening that i posted the thread i fell ill and had to be taken to hospital.i am under dialysis and my health had for sometime has not been good in spite of the treatment. That said,my equationwas to find where the reponse curve cuts the 0dB line as the slope from the third break frequency falls down at -60dB rate.The solution is to plot Bode points but the equation is tedious and unless it is done on a computer with an appropriate program i can not solve it,hence recourse to your help,the maths experts out there.thanking you in advance.
Hi to u all.sorry for late reply.that same evening that i posted the thread i fell ill and had to be taken to hospital.i am under dialysis and my health had for sometime has not been good in spite of the treatment. That said,my equationwas to find where the reponse curve cuts the 0dB line as the slope from the third break frequency falls down at -60dB rate.The solution is to plot Bode points but the equation is tedious and unless it is done on a computer with an appropriate program i can not solve it,hence recourse to your help,the maths experts out there.thanking you in advance.
This is what computers are for.
Actually it can be done on graph-paper or a spreadsheet (even paper). But I agree this is computerwork.
> where the reponse curve cuts the 0dB line
You do not specify the gain; how far it must fall to reach zero. But you can read the graphs.
I hope you get better. Soon.
Actually it can be done on graph-paper or a spreadsheet (even paper). But I agree this is computerwork.
> where the reponse curve cuts the 0dB line
You do not specify the gain; how far it must fall to reach zero. But you can read the graphs.
I hope you get better. Soon.
