These were used in lots of popular quality electronics of the 1990s, like Denon, Yamaha and such, and maybe a little earlier (can't remember) and worked just fine. Today we would want something that plugs into the same 8-pin socket but has no significant bias current and maybe a little more speed. Everybody's hot for the 50MHz GBP stuff, but I have to wonder if the improvement is worth the practical (PS bypassing impedance and bandwidth requirements, surprising new stability issues from source impedance, circuit wiring demands, yada yada) penalties, for a phono stage.
In between are devices like the OPA 2134, etc. Are there compelling reasons for something "better"?
All good fortune,
Chris
In between are devices like the OPA 2134, etc. Are there compelling reasons for something "better"?
All good fortune,
Chris
As noted CMRR and Ksvr for 5532/34 will typically be around 70 to 100 dB
With gain involved for application and power supply noise
expect a realistic number on the lower side.
You will be fine.
With gain involved for application and power supply noise
expect a realistic number on the lower side.
You will be fine.
Let me side-step for a moment, but let me check.
In a book by Toru Kuroda, a technically reliable author in my country, it is written that the equivalent noise bandwidth from 20 Hz to 20 kHz is 3200 Hz, so I use that value for verification of my own equipment, etc.
If Marcel's calculations are the same, he probably just rounded to two significant digits, which is easy to remember. (a difference of only 0.0257 dB)
I should originally calculate the value myself, but being a lazy person who is not good at calculations, I trust the value and use it as it is.😆
I have calculated the equivalent noise bandwidth of A-weighted only by myself in the past: 13.7 kHz when integrating up to 20 kHz, and about 17 kHz when integrating to infinity (although it was numerical integration using Excel, so it must have been terminated when the number stopped increasing). I remember that it was about 17 kHz when integrated to infinity.
Was the RIAA + A-weighted equivalent noise bandwidth of 3219 Hz an integral up to 20 kHz?
In a book by Toru Kuroda, a technically reliable author in my country, it is written that the equivalent noise bandwidth from 20 Hz to 20 kHz is 3200 Hz, so I use that value for verification of my own equipment, etc.
If Marcel's calculations are the same, he probably just rounded to two significant digits, which is easy to remember. (a difference of only 0.0257 dB)
I should originally calculate the value myself, but being a lazy person who is not good at calculations, I trust the value and use it as it is.😆
It's fine. JIS-A in our country just follows IHF-A (now IEC6・・・・I forgot).
I have calculated the equivalent noise bandwidth of A-weighted only by myself in the past: 13.7 kHz when integrating up to 20 kHz, and about 17 kHz when integrating to infinity (although it was numerical integration using Excel, so it must have been terminated when the number stopped increasing). I remember that it was about 17 kHz when integrated to infinity.
That 3219 Hz is for IEC modified RIAA and A-weighting integrated from 1 Hz to 1 MHz. I also have numbers without IEC modification (that is, without 20 Hz first-order high-pass) and from 20 Hz to 20 kHz, but I don't know those values by heart.
For only A-weighting, I got about 12.5 kHz integrating up to 20 kHz and about 13.5 kHz integrating up to 1 MHz.
For only A-weighting, I got about 12.5 kHz integrating up to 20 kHz and about 13.5 kHz integrating up to 1 MHz.
Last edited:
I am surprised that both Mr Kuroda's RIAA+A-weighted values and my A-weighted values are very different from Marcel's.
My calculated transfer function of A-fil is
1.2589/(1+13.052u*s)^2*1/(1+4636.36/s)*1/(1+676.7/s)*1/(1+129.433/s)^2
and the time constants are
LPF: 13.052us^2
HPF: 215us, 1477.75us, 7726us^2
but are they different from Marcel's?
My calculated transfer function of A-fil is
1.2589/(1+13.052u*s)^2*1/(1+4636.36/s)*1/(1+676.7/s)*1/(1+129.433/s)^2
and the time constants are
LPF: 13.052us^2
HPF: 215us, 1477.75us, 7726us^2
but are they different from Marcel's?
This is my whole list. For RIAA- and A-weighting, the noise bandwidth relative to the gain at 1 kHz that I found is always between 3212.71 Hz and 3220.23 Hz, depending on the integration limits and the IEC amendement. I don't know how accurate the numerical integration was; probably fairly accurate, but the numbers after the decimal point can easily be off. Besides, two of the A-weighting corner frequencies were about 0.05 % too high, as shown below. Anyway, it's all pretty close to 3.2 kHz.
I used LTSpice for the numerical integration, using this circuit and these expressions:
My A-weighting filter therefore consisted of four first-order high-pass stages and two first-order low-pass stages. The cut-off frequencies were:
two at 20.6 Hz (time constant 7.725968111 ms)
one at 107.7 Hz (time constant 1.477761774 ms)
one at 737.9 Hz (time constant 215.6863303 μs)
two at 12.2 kHz (time constant 13.04548714 μs)
Looking at https://en.wikipedia.org/wiki/A-weighting , I see that that 12.2 kHz should really have been 12194 Hz, the rest matches.
Last edited:
Thank you for your answer.
Since you said that the time constants and gain coefficients of the A filter are almost the same, I checked the simulation and it seems that my numerical integration was still wrong.
I tried to find an excel file to see where I was wrong, but I couldn't find a file from 25 years ago.
I will try to calculate it again when I get the energy. (Probably won't do it)
It was good to know my mistake. Thank you
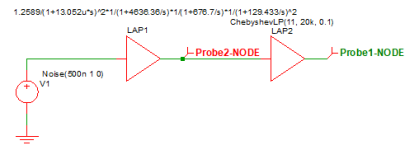
A 1Vrms noise signal source up to 1MHz (i.e. 1mV/√Hz noise) was measured RMS through an A-filter (LAP1) and an 11th order 20kHz Chebyshev filter (LAP2)
Equivalent noise bandwidth of A-filter + 20 kHz LPF
(112.415m/1m)^2=12.637kHz
Equivalent noise bandwidth of A-filter only
(117.4m/1m)^2=13.783kHz
Since you said that the time constants and gain coefficients of the A filter are almost the same, I checked the simulation and it seems that my numerical integration was still wrong.
I tried to find an excel file to see where I was wrong, but I couldn't find a file from 25 years ago.
I will try to calculate it again when I get the energy. (Probably won't do it)
It was good to know my mistake. Thank you
A 1Vrms noise signal source up to 1MHz (i.e. 1mV/√Hz noise) was measured RMS through an A-filter (LAP1) and an 11th order 20kHz Chebyshev filter (LAP2)
Equivalent noise bandwidth of A-filter + 20 kHz LPF
(112.415m/1m)^2=12.637kHz
Equivalent noise bandwidth of A-filter only
(117.4m/1m)^2=13.783kHz
